Spin-dependent amplitude and phase modulation with multifold interferences via single-layer diatomic all-silicon metasurfaces

Introduction

Since the introduction of the generalized Snell's law by Capasso et al. in 2011, there has been a proliferation of strategies for metasurface design based on abrupt phases¹. The abrupt phase can be categorized into dynamic and geometric phases according to the physical mechanism of generation^2,3. The geometric phase, also known as Berry's phase, named after physicist Michael Berry, is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes⁴⁻⁹. Currently, the geometric phase originates from the spin-orbit interactions of photons, the magnitude of which can be described by the cyclic evolutionary trajectory of the polarization state on the Poincaré sphere¹⁰⁻¹². A vortex is a type of optical beam characterized by a helical phase front and carrying orbital angular momentum (OAM), with a central phase singularity where the intensity drops to zero¹³⁻¹⁵. Geometric phases can be exploited to generate and manipulate vortex beams. By using spatially varying birefringent elements, such as those configured to impart a Pancharatnam-Berry (PB) phase, the polarization of an incident beam can be manipulated in such a way that it acquires orbital angular momentum¹⁶⁻¹⁸. The capability to generate and control vortex beams via geometric phases has significant implications in various fields, including optical trapping and manipulation, and it also presents new opportunities in communications technology¹⁹⁻²¹.

Terahertz (THz) radiation, located the microwave and infrared spectrum, offers higher bandwidth for faster data rates, but its widespread adoption requires advancements in transmitters, receivers, modulation techniques, and supporting infrastructure^19,22−26. The extensive development of all-dielectric metasurfaces provides an opportunity for miniaturization and integration of multi-functional systems²⁷⁻²⁹. Metasurfaces, as quasi-periodic arrays in the subwavelength scale, have attracted extensive research interest in photonics, such as beam focusing³⁰⁻³⁴, structured vector field generation³⁵⁻⁴⁰, and spin-dependent polarization control^18,41−44. In particular, the diatomic metasurface for performing spin-dependent wavefront shaping can be equivalently viewed as an integration of polarizers and isolators⁴⁵⁻⁵². Deng et al. reported a reflective diatomic metasurface design mechanism for active diffraction and hologram reconstruction of multiple polarization states. However, the inherent ohmic loss limits the further application of such a design in optics⁴⁵. Liang et al. designed and validated a plasmonic diatomic metasurface for mid-infrared full Stokes polarization absorption. The proposed design can provide the spectral responses of perfect absorption and total reflection for a pair of orthogonally polarized states, respectively. However, the complex configuration of the cell structure creates an obstacle for its practical application⁴⁶. Gao et al. demonstrated an all-dielectric diatomic metasurface with a conversion from arbitrary to linear polarization at an operating wavelength of 690 nm. However, a rigorous mathematical analysis using the Jones matrix imposes limitations on the wavefront modulation achievable by this design strategy. This constraint makes it challenging to develop a deeper physical understanding of the underlying mechanisms involved⁴⁸.

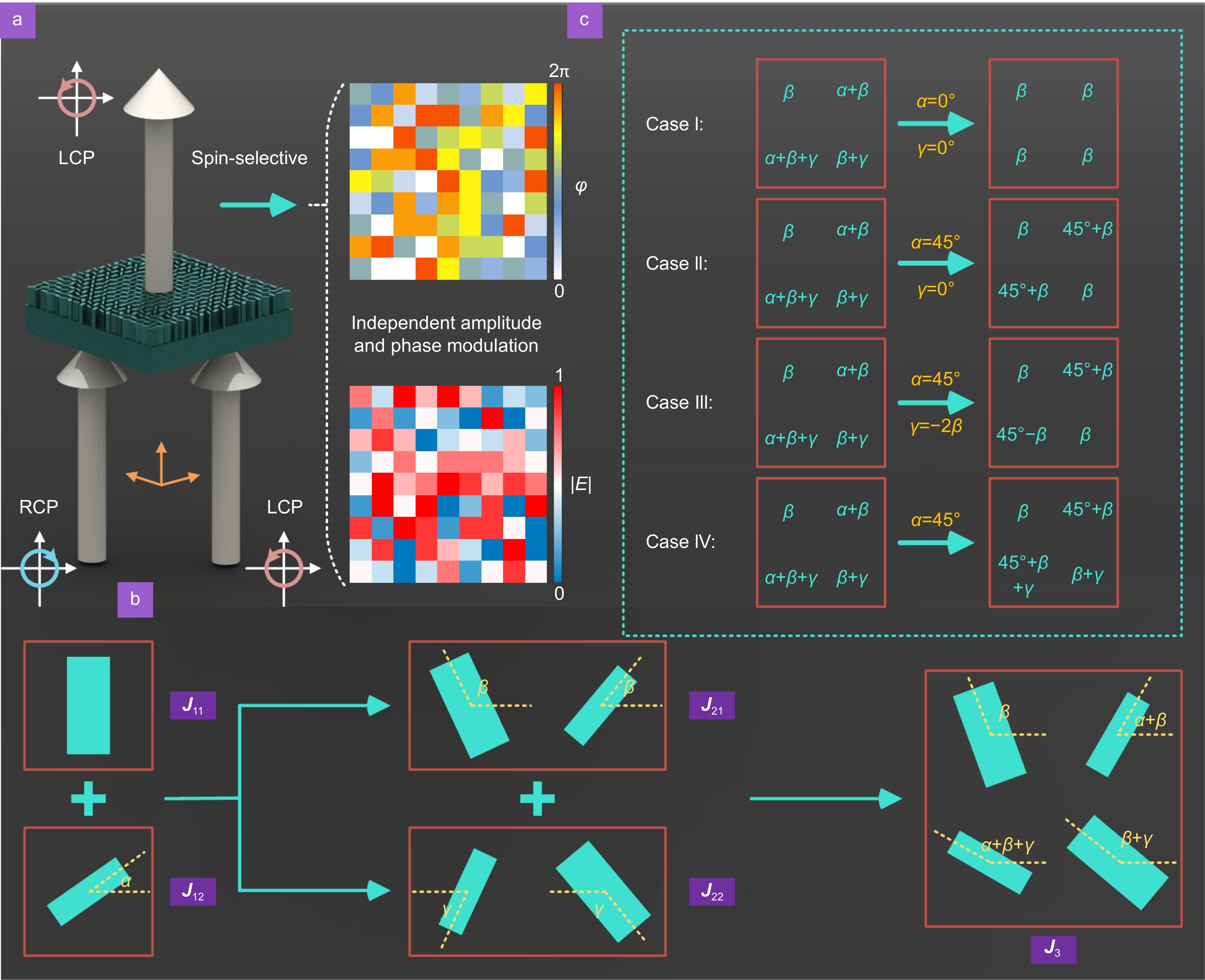
This study presents a multiple geometrical phase mechanism, utilizing the Jones matrix, which grants a high degree of freedom to the metasurface. This mechanism exhibits spin-selective transmission behavior and can further facilitate wavefront shaping within orthogonal circularly polarized channels, as illustrated in Fig. 1(a). The implementation of multifunctional diatomic metasurfaces is demonstrated in the THz range by utilizing a pair of HWP (half-wave plate) meta-atoms with birefringent effects. Specifically, the physical implications of each degree of freedom are enforced through the stepwise superposition principle, determined by the parameters α, β and γ, respectively, as displayed in Fig. 1(b). Consequently, a rigorous theoretical prediction of the spin-dependent modulation can be made by executing this design strategy in the THz band, as shown in Fig. 1(c). In case I, metasurfaces that can produce THz holography are assembled by utilizing the Gerchberg-Saxton algorithm for classical purely geometric phase modulation. In case II, the extreme values of the asymmetric transmission (AT) parameter were further evaluated by adjusting the relative rotation angles between the meta-atoms in the four quadrants. In other words, a supercell determined by the parameter β can realize spin-dependent pure phase modulation. In case III, THz near-field imaging of diatomic metasurfaces is verified with a design strategy possessing pure amplitude modulation. Subsequently, the THz meta-lens was evaluated in case IV with a generalized complex amplitude modulation behavior. Accordingly, the proposed diatomic assembly strategy can provide a powerful platform for applications such as bio-imaging, optical data storage, and information encryption.

Figure  1.  Full-Size Img PowerPoint

(a) Working principle of the proposed design under orthogonal circularly polarized THz beam illumination with spin-selective properties. (b) The assembly process of the metamolecule consists of the stepwise superposition of a pair of HWP meta-atoms with a phase difference of 90°. (c) Four parametric conditions with classical geometric phase modulation, pure phase modulation with spin selectivity, pure amplitude modulation with spin selectivity, and complex amplitude modulation with spin selectivity, respectively.

Metasurface implementation

A pair of meta-atoms with a defined phase difference is applied to assemble the desired diatomic metasurfaces, as shown in Fig. 1(b). Here, the electromagnetic response of each meta-atom with structural birefringent behavior is analogous to a half-wave plate (HWP). Thus, the Jones matrix for describing the transmission process in the circularly polarized basis can be written as^16,53,

here, $\sigma = \pm 1$ denotes the spin state, and the subscripts R and L denote the RCP and LCP channels, respectively. ${T_{{\rm{RR}}}}$ (${T_{{\rm{LL}}}}$) and ${T_{{\rm{LR}}}}$ (${T_{{\rm{RL}}}}$) denote the extracted complex coefficients in the co-polarized and cross-polarized channels under RCP (LCP) illumination, respectively. The concept of geometric phase introduces a fundamental aspect of phase that stems from the geometry of the system's pathway through its state space. Subsequently, a standard rotation matrix $R\left( \theta \right)$ is implemented for characterizing such a silicon pillar rotating along the z-axis at angle $\theta$. The value of the geometric phase produced on the Poincaré sphere during the polarization evolution from the LCP to the RCP is then equal to half of the stereo angle corresponding to the closed path surrounded by the circular evolution, i.e., ${\theta \mathord{\left/ {\vphantom {\theta {2\pi \times 4\pi = 2\theta }}} \right. } {2{\mathrm{\pi}} \times 4{\mathrm{\pi}} = 2\theta }}$⁵⁴⁻⁵⁷. On the contrary, in case of an evolution from RCP to LCP, the value of the resulting geometric phase is $- 2\theta$. It is assumed that this HWP meta-atom exhibits equal normalized amplitudes across the orthogonal circularly polarized channels. Thus, the Jones matrix of the geometric phase produced by a HWP meta-atom with a rotation angle θ in the circularly polarized basis can be written as^58,59,

Taking the rectangular pillar represented by ${{\bf{J}}_{11}}$ as a reference and setting $\theta = {0^{\circ} }$, then ${{\bf{J}}_{11}}$ can be expressed as,

By utilizing the HWP meta-atom characterized by J₁₂ as an additional degree of freedom, we observe that, in comparison to the reference, the new configuration introduces a rotation angle, denoted as α, and a relative phase delay, represented by δ. Consequently, J₁₂ can be articulated as,

The employed HWP meta-atoms can be considered as truncated waveguides, allowing for the neglect of coupling effects between adjacent silicon pillars. In other words, the interference mechanism arises independently of the placement of the meta-atoms in space. Consequently, the Jones matrix ${\bf{J}_{21}}$ for a supercell constructed from two meta-atoms exhibiting a constant phase difference can be derived through a mathematical superposition operation, typically expressed as^48,49,

Apparently, the phase retardations generated by the supercells within the cross-polarized channels under LCP and RCP illumination are $\delta + 2\alpha$ and $\delta - 2\alpha$. According to the interference mechanism, a supercell that satisfies the phase enforcement condition $\left\{ \begin{gathered} \delta + 2\alpha = {\mathrm{\pi}} \\ \delta - 2\alpha = 0 \\ \end{gathered} \right.$ can produce broadband AT parameters, i.e., $\max \left( {{\rm{AT}}} \right){\rm{ = }}{T_{{\rm{LR}}}} + {T_{{\rm{RR}}}} - {T_{{\rm{RL}}}} - {T_{{\rm{LL}}}}$. Through simple calculations, when $\delta = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}$ and $\alpha = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {\pi 4}} \right. } 4}$, AT reaches its maximum value⁶⁰⁻⁶³. The parameter δ is fixed to ${{\mathrm{\pi}} \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}$ in order to achieve multi-dimensional polarization manipulation with the assistance of the geometric phase mechanism. Then, ${{\bf{J}}_{21}}$ can be further simplified as,

The supercell characterized by the matrix ${J_{21}}$ is determined by the key parameter α. In other words, by adjusting the phase parameter α, the amplitude of the AT can be modulated in the transmission mode. To further enable the proposed design to realize the modulation of both amplitude and phase, ${{\bf{J}}_{21}}$ is endowed with another rotation angle β given by the standard rotation matrix, then ${{\bf{J}}_{21}}$ can be expressed as,

here, the additional rotation angle β can be used for phase modulation within the orthogonal circular polarization channel. Subsequently, by treating the supercell as a new element and giving it a rotation angle γ with respect to ${{\bf{J}}_{21}}$, the Jones matrix ${{\bf{J}}_{22}}$ can be calculated as,

By combining the matrices (7) and (8), the assembled metamolecule can be made to contain a total pair of HWP meta-atoms with a phase difference of $\delta = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 2}} \right. } 2}$, as shown in Fig. 1(b). Then the total Jones matrix can be calculated as,

The interference mechanism imparts the same physical significance to the rotation angles γ and α, and further limits the phase difference between the two supercells. Simultaneous modulation of transmitted amplitude and phase can be achieved by rationally configuring the relative rotation angles between neighboring meta-atoms. Thus, the total transmission coefficient in the orthogonal circularly polarized channels can be described as⁵⁸,

In the global coordinate system, the four meta-atoms satisfying the interference mechanism are coincident in space, so their positions in the four quadrants can be arbitrarily tailored. Moreover, the distance between neighboring meta-atoms is consistent with the lattice period. As shown in Fig. 1(b), the relative rotation angles of the four HWP meta-atoms can be described as $\beta$, $\alpha + \beta$, $\beta + \gamma$ and $\alpha + \beta + \gamma$, respectively. To further demonstrate the proposed multifunctional diatomic metasurface, the independent modulation of the amplitude and phase of the incident THz beam is depicted in Fig. 1(c) for different cases, respectively. As an example, the modulation process within the RCP→LCP channel (${T_{{\rm{LR}}}}$) is calculated for each of the four cases. Setting the parameter $\alpha = \gamma = 0$, there is no relative rotation angle between the individual HWP meta-atoms. Then, the transmission coefficient ${T_{{\rm{LR}}}}$ can be further simplified to ${T_{{\rm{LR}}}} = {\rm{exp }}\left( { - {\mathrm{i}}2\beta } \right)$. In other words, the metamolecule degenerates into meta-atoms with anisotropy determined by the parameter $\beta$. Therefore, pure geometric phase modulation of the incident THz beam can be realized by changing the parameter $\beta$. Setting the parameters $\alpha = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 4}} \right. } 4}$ and $\gamma = 0$ implies that the relative angle between the pair of meta-atoms for assembling the metamolecule is ${{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 4}} \right. } 4}$. The transmission coefficient ${T_{{\rm{LR}}}}$ can be further simplified to ${T_{{\rm{LR}}}} = {\rm{exp }}\left( { - {\mathrm{i}}2\beta } \right)$. Thus, the resulting constructive and destructive interference mechanisms can be employed to achieve spin-dependent pure phase modulation. Setting parameters $\alpha = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 4}} \right. } 4}$ and $\gamma = - 2\beta$, the transmission coefficient ${T_{{\rm{LR}}}}$ can be further calculated as ${T_{{\rm{LR}}}} = {\cos }\left( {2\beta } \right)$. Thus, such parametric conditions allow for pure amplitude modulation behavior. Not surprisingly, when the parameter $\alpha = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 4}} \right. } 4}$, simultaneous variation of $\beta$ and $\gamma$ can achieve spin-dependent complex amplitude modulation. After a simple calculation, the parameter ${T_{{\rm{LR}}}}$ can be expressed as ${T_{{\rm{LR}}}} = \dfrac{1}{2}\left[ {{\rm{exp }}\left( { - {\mathrm{i}}2\beta } \right) + {\rm{exp }}\left( { - {\mathrm{i}}2\left( {\beta + \gamma } \right)} \right)} \right]$. Therefore, by rationally matching the rotation angles $\beta$ and $\gamma$, the proposed design can perform wavefront manipulation at different transmission intensities. The designed diatomic metasurface MS determined by the incident spin state can be considered as an operator ${\hat {Π} _{{\mathrm{MS}}}}$ and the implementation process can be described as ${\hat {Π} _{\mathrm{MS}}}\left| {{\sigma _{\rm{R}}}} \right\rangle = {\rm{exp }}\left[ {{\mathrm{i}}\left( {{\varphi _f} + {\varphi _v}} \right)} \right]\left| {{\sigma _{\rm{L}}}} \right\rangle$, as shown in Fig. 1(a). Here, ${\varphi _f}$ and ${\varphi _v}$ indicate the focusing and spiral phase profiles, respectively. In general, the phase distributions ${\varphi _f}$ and ${\varphi _v}$ can be expressed as⁶⁴⁻⁶⁶,

where $r = \sqrt {{x^2} + {y^2}}$, and $\phi = {\rm{arctan}}\left[2\left( {y,x} \right)\right]$ denote the radius and azimuth angle of polar coordinate, respectively, $l$ is the number of topological charges.

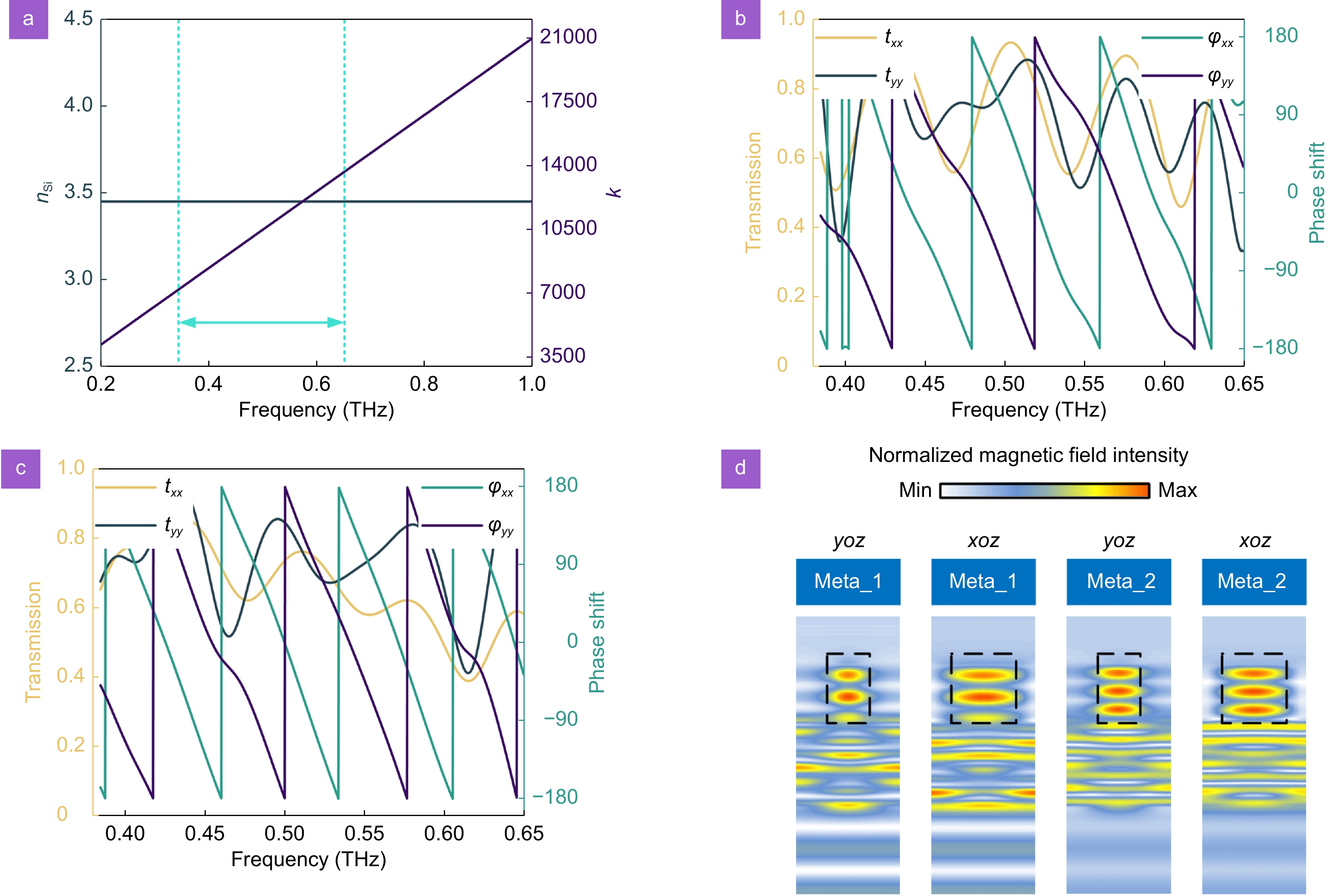
Silicon materials with high resistivity and low absorption loss are selected as candidates for realizing complex amplitude modulation with spin-selective properties in the desired THz range⁶⁷. As shown in Fig. 2(a), the refractive index of silicon in the labeled THz range is a constant, i.e., n_Si = 3.45. The corresponding wave vector k is also depicted in Fig. 2(a). It can be clearly seen that silicon materials with sufficiently high refractive indices can fulfill the design requirements for phase coverage from 0 to 2π. The transmission amplitude and phase distributions of HWP meta-atoms with periodic boundary conditions along the x- and y-axes, corresponding to rectangular silicon pillars in the metamolecule in the first (third) and second (fourth) quadrants, respectively, are then illustrated in Fig. 2(b) and 2(c). At the same time, the z-axis along the metamolecule is set to the open (add space) boundary condition. Numerical simulation results show that each HWP meta-atom has π phase difference and uniform amplitude at 0.5 THz under orthogonal linearly polarized illumination. Also, the phase difference between neighboring HWP meta-atoms is π/2. Subsequently, the magnetic field distribution of each HWP meta-atom was obtained and normalized using field monitor calculations. The normalized magnetic field distributions corresponding to both the xoz and yoz planes, respectively, indicate that the energy carried by the incident THz beam is bound inside the silicon pillars with high refractive index^68,69. Such a behavior indicates that the coupling effects between neighboring meta-atoms can be neglected, ensuring the efficiency of the metasurfaces assembled based on discrete phases, as shown in Fig. 2(d).

Figure  2.  Full-Size Img PowerPoint

(a) Refractive index of high-resistance silicon and wave vectors in the working frequency band. The HWP meta-atoms selected for the organization of the metamolecule, denoted as (b) Meta_1 and (c) Meta_2, have a constant phase difference δ=π/2, respectively. (d) Normalized magnetic field distributions collected within the xoz and yoz planes, respectively, corresponding to a pair of HWP meta-atoms Meta_1 and Meta_2.

Results and discussion

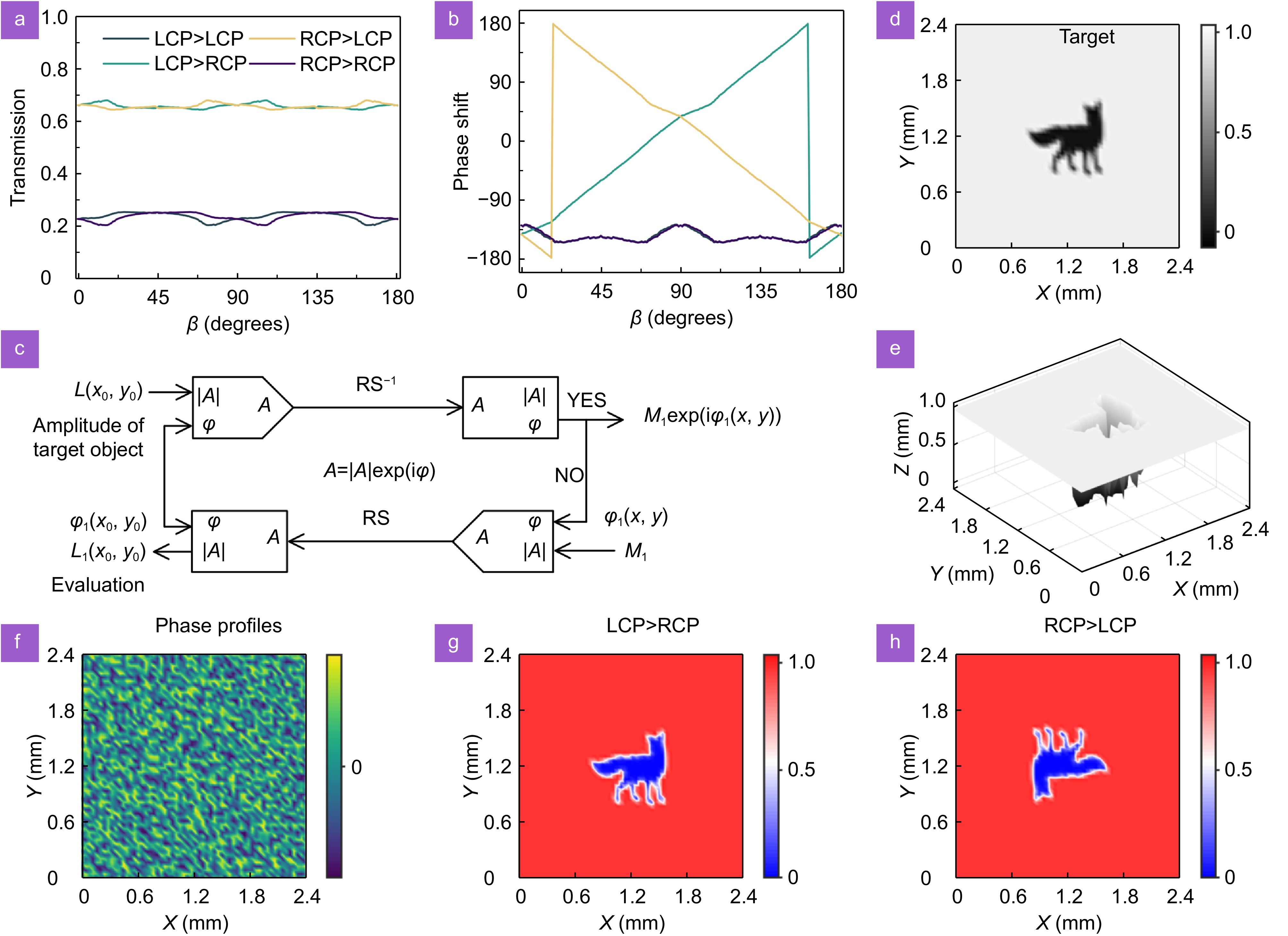
By setting parameter $\alpha = \gamma = 0$, the wavefront modulation can be empowered by the classical geometric phase and determined by parameter $\beta$. Amplitude curves for the LCP→LCP, LCP→RCP, RCP→LCP, and RCP→RCP channels were obtained by systematically increasing the parameter while periodically distributed metamolecules were illuminated by an orthogonal circularly polarized beam. As shown in Fig. 3(a), the mean value of the amplitudes collected in the cross-polarized channel is greater than 0.67 while the amplitudes in the co-polarized channel are less than 0.22. Not only that, RCP and LCP excitations produce phase parameters with opposite evolutionary trends within the cross-polarized channel, further illustrating the working mechanism of the geometric phase, as depicted in Fig. 3(b). And the THz holography based on the geometric phase mechanism was assembled by utilizing the standard Gerchberg-Saxton algorithm^70,71, as shown in Fig. 3(c). An image featuring a fox pattern, illustrated in Fig. 3(d), was utilized as a candidate for assessing the performance of THz holography. Initially, the original image must be converted into a format suitable for holographic display. This process typically involves normalizing the image by transforming the pixel values into phase information, as illustrated in Fig. 3(e). Following this, the raw image requires further sampling using the Gerchberg-Saxton algorithm to align with the pixel size and spacing of the metasurface, ensuring proper resolution compatibility. Figure 3(f) illustrates the phase distribution associated with the diatomic metasurface. Subsequently, the metasurface array was processed by utilizing the commercial simulation software CST Studio Suite. The x-, y- and z-directions along the metasurfaces were set as open boundary conditions. The resulting THz holographic images are presented in Fig. 3(g) and 3(h), which correspond to the channels LCP→RCP and RCP→LCP, respectively. Notably, the holograms captured in different orthogonal circularly polarized components exhibit opposite configurations, aligning with the design strategy.

Figure  3.  Full-Size Img PowerPoint

(a) Amplitude and (b) phase delay corresponding to geometric phase modulation obtained by scanning the parameter factor β, including LCP→LCP, LCP→RCP, RCP→LCP, and RCP→RCP channels. (c) GS algorithm flow used to perform THz hologram imaging, (d) target image, (e) processed image. (f) Phase distribution corresponding to the target image. (g) THz hologram images in the LCP→RCP and (h) RCP→LCP channels obtained by utilizing the time-domain solver.

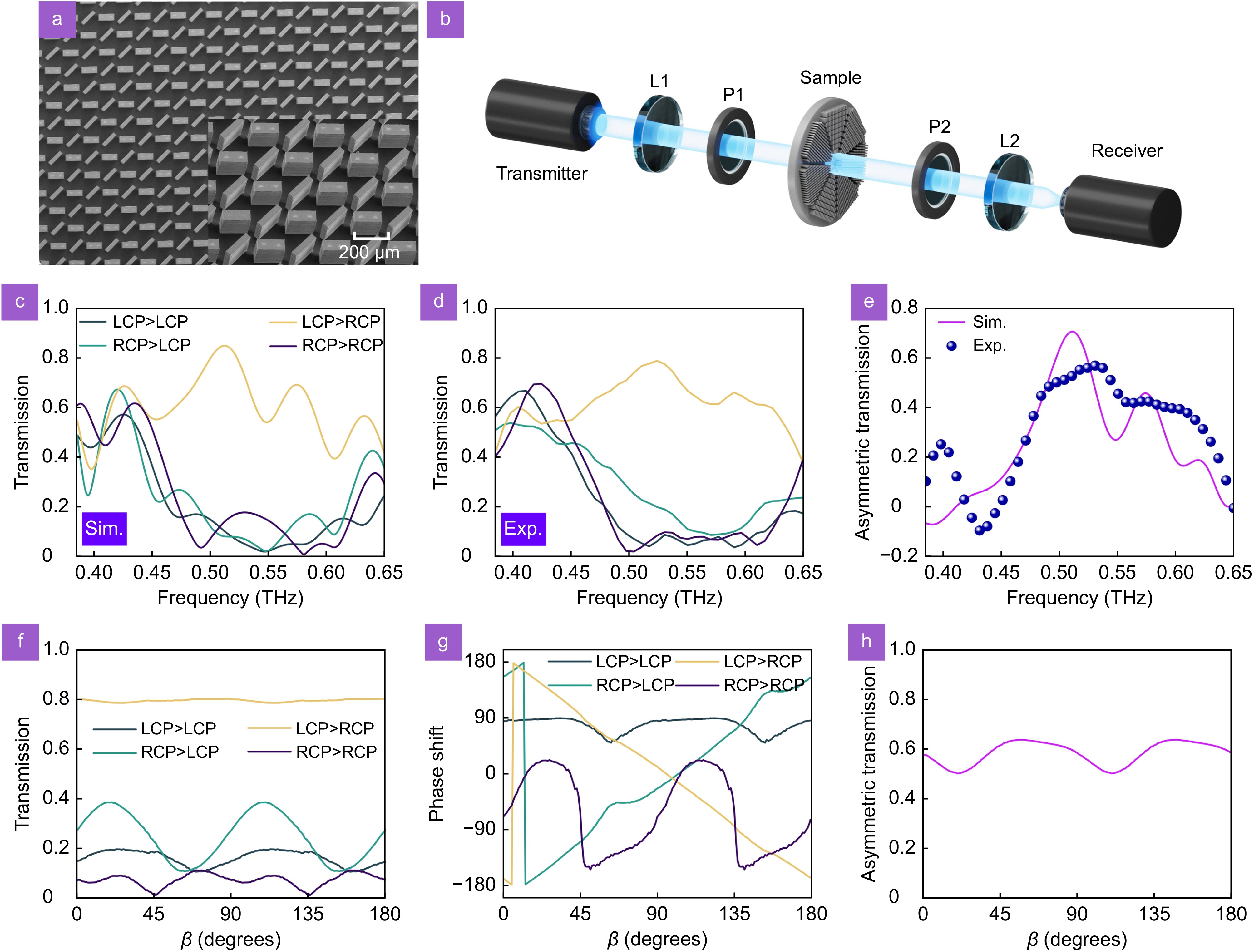
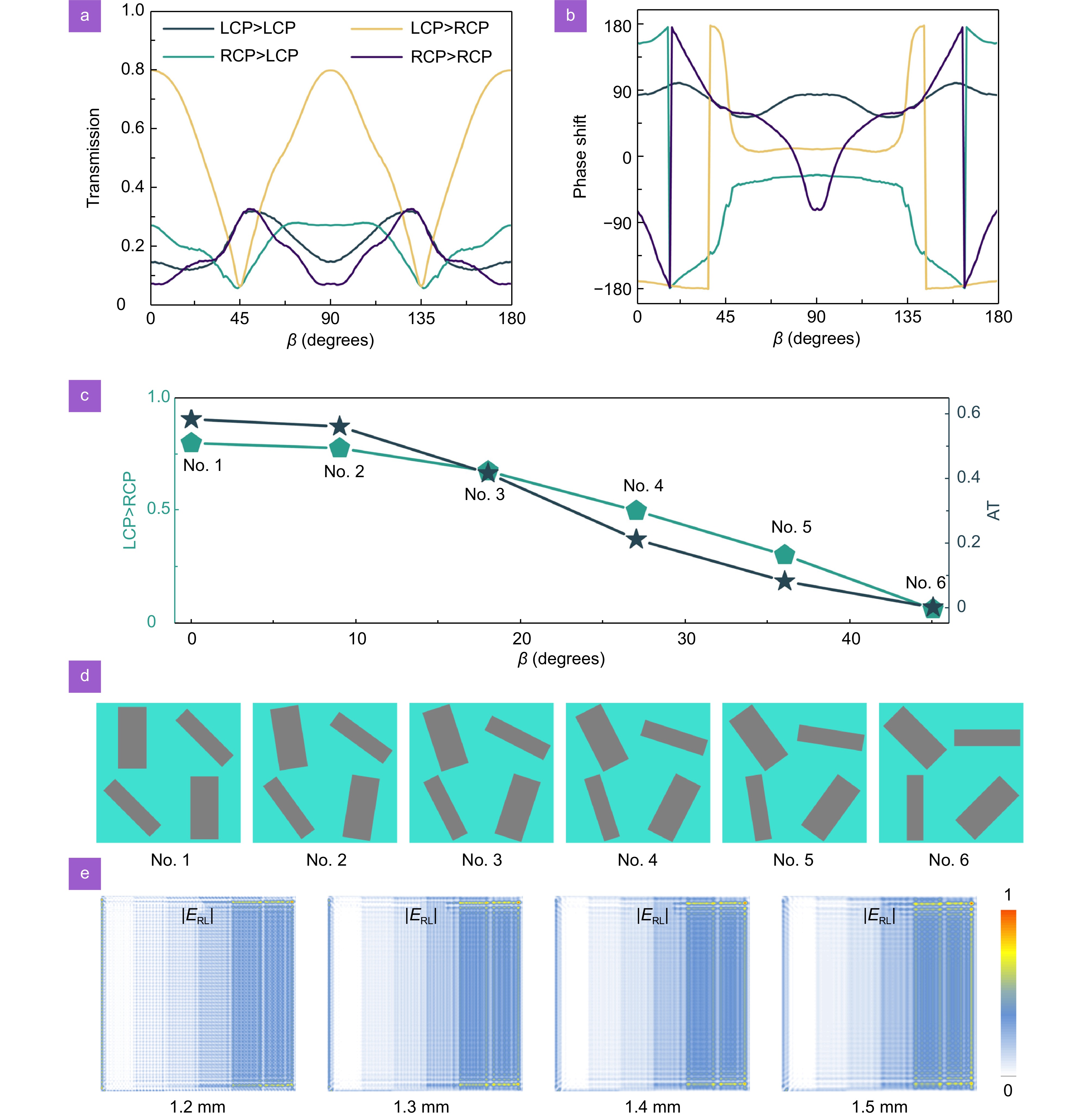
Setting parameters $\alpha = {{\mathrm{\pi}}/ 4}$ and $\gamma = 0$, the relative rotation angle between neighboring HWP meta-atoms in the designed metamolecule is π/4, the proposed design strategy can be simplified to pure phase modulation with spin-selective properties. According to the interference mechanism, the maximum and minimum values of transmission amplitudes within the LCP→RCP and RCP→LCP channels, respectively, can be achieved for the optimal AT parameters. To further illustrate the broadband response with spin-selective properties generated by these diatomic metasurfaces, high-resistance silicon wafers with a thickness of 1 mm were processed using standard UV lithography and inductively coupled plasma (ICP) etching techniques. Benefiting from the non-dispersive refractive index and low absorption loss exhibited by high-resistance (resistivity>10⁴ Ω·cm) silicon wafers in the THz band. The obtained scanning electron microscope (SEM) image labeled as Sample I is shown in Fig. 4(a). Photographs of the samples at different scales all show well-finished accuracy with smooth surfaces and steep sidewalls. The transmission spectrum under circularly polarized THz beam illumination was measured by further employing a terahertz time-domain spectroscopy (TDS) system, as shown in Fig. 4(b). The THz beam generated by the emitter is collimated by a lens labeled as L1 and then illuminated onto the substrate of Sample I. The THz beam passing through the metasurface sample is focused by a lens labeled as L2 and further transmitted to the receiver for analysis. Polarizers labeled as P1 and P2 are introduced to adjust the polarization states of the incident and transmitted THz beams, respectively, in order to obtain the desired components. The spin-dependent transmission amplitudes obtained in simulation and experiment are shown in Fig. 4(c) and 4(d), respectively. As we observed, the metasurface sample produces a much larger amplitude in the LCP→RCP channel than the other three components. Subsequently, the AT parameters were calculated from the transmission coefficients, corresponding to the simulation and experimental results, respectively, as shown in Fig. 4(e). The simulation and the experiment are consistent. Benefitting from the Fabry-Perot resonance due to the large thickness of the substrate, the maximum value of the AT parameter can reach 0.72.

Figure  4.  Full-Size Img PowerPoint

(a) Sample I obtained by utilizing the ICP etching technique when α = π/4, β = 0, and γ = 0. (b) THz TDS system for performing sample measurement tasks. (c) Simulation and (d) experimental results of transmitted polarization conversion for two spins when α = π/4, β = 0, and γ = 0. (e) AT spectra containing both simulation and experimental results. (f) Amplitude, (g) phase delay, and (h) AT parameter corresponding to spin-dependent pure phase modulation obtained by scanning the parameter factor β.

Amplitudes with spin-selective properties were further evaluated by continuously increasing $\beta$ from 0° to 180°, as shown in Fig. 4(f). The amplitude collected within the LCP→RCP channel remains almost constant (~0.8) and is much higher than the remaining three components. As $\beta$ gradually increases, the phase distribution within the LCP channel satisfies the phase coverage from −180° to 180° with a smooth evolution trend, as shown in Fig. 4(g). Consequently, the mean value of the AT parameter, obtained through additional processing, is approximately 0.58, which reflects the spin-dependent polarization features, as displayed in Fig. 4(h).

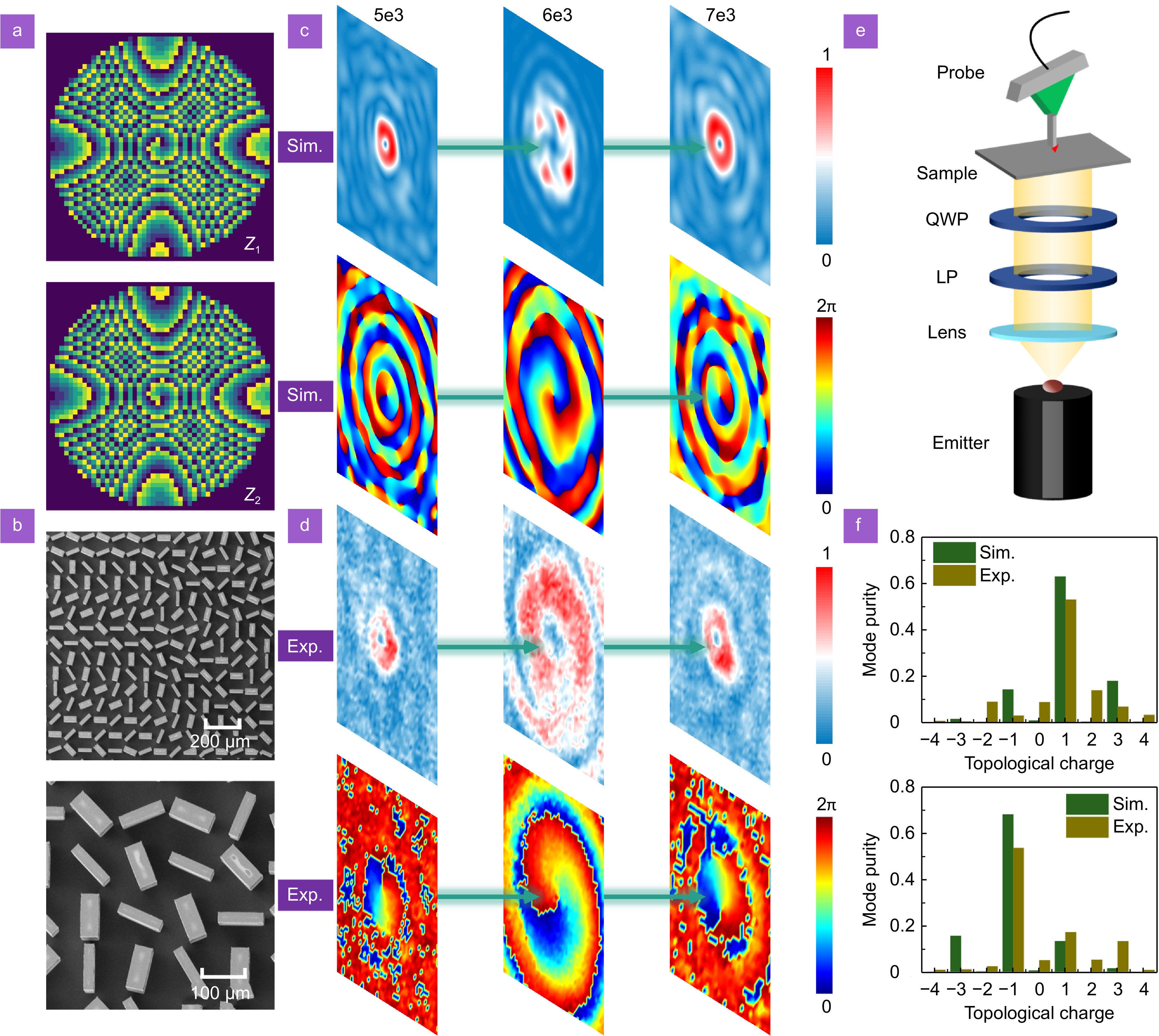
Given the wide range of application requirements for metasurfaces with spin-selective properties, the generation of focused vortex beams with longitudinal topological charge evolution behavior is further explored by performing polarization multiplexing encoding techniques. As described in Eq. (11), the phase profile embedded at the plane of f₁ = 5 mm is ${\Phi _1} =A{\rm{exp}}\left[ {{\mathrm{i}}\left( {{\varphi _{f1}} + {\varphi _{v1}}} \right)} \right]$ while the phase distribution embedded at the plane of f₂ = 7 mm is ${\Phi _2} = A{\rm{exp}}\left[ {{\mathrm{i}}\left( {{\varphi _{f2}} + {\varphi _{v2}}} \right)} \right]$. Here, A is the transmission amplitude of the metasurface and is assumed to be 1 when only phase modulation is considered, the key parameters l₁ and l₂ that determine the spiral phase profiles ${\varphi _{v1}}$ and ${\varphi _{v2}}$, respectively, are set to −1 and +1. The phase distributions at the f₁ = Z₁ and f₂ = Z₂ planes were calculated by using a joint simulation method (driven by MATLAB), as shown in Fig. 5(a), respectively. The desired metasurface samples were processed by utilizing standard ICP etching techniques, labeled as Sample II, and the resulting SEM photographs are shown in Fig. 5(b). Indeed, the implementation mechanism of a focused vortex beam generator with spin-selective properties under LCP illumination can be described as ${\hat \Pi _{{\rm{II}}}}\left| {{\sigma _{\rm{L}}}} \right\rangle = {\rm{exp }}\left[ {{\mathrm{i}}\left( {{\varphi _{f1}} + {\varphi _{v1}}} \right)} \right]\left| {{\sigma _{\rm{R}}}} \right\rangle$ and ${\hat \Pi _{{\rm{II}}}}\left| {{\sigma _{\rm{L}}}} \right\rangle = {\rm{exp }}\left[ {{\mathrm{i}}\left( {{\varphi _{f2}} + {\varphi _{v2}}} \right)} \right]\left| {{\sigma _{\rm{R}}}} \right\rangle$, corresponding to the Z₁ and Z₂ planes, respectively. Numerical simulation results show that the electric field extracted on Z₁ = 5 mm and Z₂ = 7 mm planes exhibit doughnut-shaped intensity distributions, respectively. Meanwhile, the Z = 6 mm plane shows a transition state, reflecting the evolutionary behavior of the topological charge over a finite propagation distance in the longitudinal direction, as displayed in Fig. 5(c). The phase distributions captured by the field monitor, at both the Z₁ = 5 mm and Z₂ = 7 mm planes are illustrated in Fig. 5(c). As we observed, the topological charge gradually evolves from l₁ = −1 to l₂ = +1. The electric field intensity and phase distributions measured in the experiments are shown in Fig. 5(d), respectively, which are consistent with the simulation results. It is worth emphasizing that the experimental results were obtained by using a near-field detection system equipped with THz microprobes, as shown in Fig. 5(e). The THz pulse emitted from the emitter is first collimated by Lens and carries the desired polarization state after passing through the LP and QWP. The mode purity of vortex states carrying different topological charges at the focal plane can be further calculated using the standard Fourier transform. In fact, the mode purity of vortex beams is defined as the ratio of the power of the primary mode to the total power of all modes. Therefore, it is essential to first compute the OAM spectral function A_l along with the sampling phase α(ϕ). Their respective expressions are as follows:

Figure  5.  Full-Size Img PowerPoint

(a) Spiral phase distributions embedded in the Z₁=5 mm and Z₂=7 mm planes. (b) Sample II obtained by utilizing the ICP etching technique. (c) Simulation and (d) experimental results extracted in different planes along the propagation direction, including the electric field intensity and phase distribution. (e) THz near-field detection system for capturing the focal field distribution. (f) The mode purity calculated in the Z₁ and Z₂ planes, respectively.

where ϕ is periodic function, exp(ilϕ) represents a spiral harmonic. The mode purity at the Z₁ and Z₂ planes is calculated in Fig. 5(f), including simulation and experimental results, respectively. As we observed, the number of topological charges l₁ = +1 and l₂ = −1 dominate the mode purity in the Z₁ and Z₂ planes.

Setting the parameters $\alpha = {{\mathrm{\pi}}/4}$ and $\gamma = - 2\beta$, the extracted transmission amplitude within the cross-polarized channel can be simplified to ${T_{{\rm{LR}}}} = {\cos }\left( {2\beta } \right)$. As illustrated in Fig. 6(a), the amplitude within the LCP channel follows the trend of a cosine function as the parameter $\beta$ gradually increases from 0° to 180°. Conversely, the extracted phase distribution is misaligned, rendering it ineffective for implementing wavefront manipulation, as displayed in Fig. 6(b). Therefore, these parametric conditions are realized through pure amplitude modulation with spin-selective characteristics. Leveraging the principle of interference, six metamolecules were meticulously arranged at intervals of Δβ = 9° to facilitate THz near-field imaging. The transmission amplitudes and AT parameters of the selected metamolecules exhibit a linearly decreasing trend, as illustrated in Fig. 6(c). Additionally, the top views of the various metamolecules are presented in Fig. 6(d). The different relative rotation angles among the individual HWP meta-atoms effectively facilitate pure amplitude modulation within the LCP→RCP channel. Following this, an array for THz near-field imaging was constructed by sequentially selecting metamolecules with distinct amplitudes, and its imaging performance was simulated using a time-domain solver. Figure 6(e) illustrates that the |E_RL|—component of the electric field intensity extracted in the LCP→RCP channel exhibits progressively enhanced near-field imaging effects from left to right. Moreover, the near-field images reconstructed over a finite distance along the propagation direction achieve the desired performance.

Figure  6.  Full-Size Img PowerPoint

(a) Amplitude and (b) phase shift corresponding to spin-dependent pure amplitude modulation obtained by scanning the parameter factor β. (c) The extracted amplitudes within the LCP→RCP channel and the calculated AT parameters at intervals of Δβ = 9°, respectively. (d) Top view of the six metamolecules selected for performing pure amplitude shaping. (e) The electric field distribution |E_RL| corresponding to THz near-field imaging extracted over a finite distance from 1.2 mm to 1.5 mm along the z-direction.

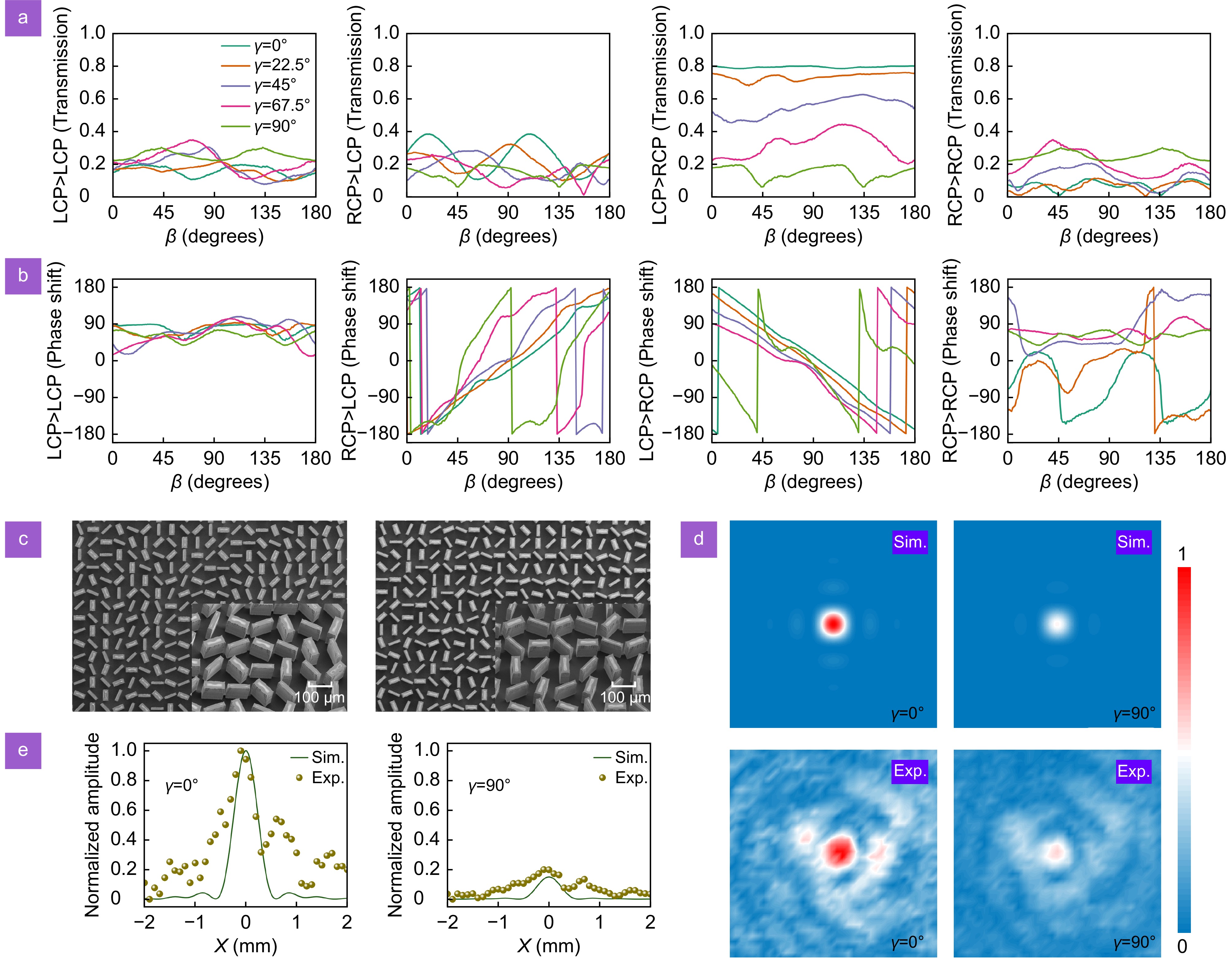
Setting parameter $\alpha = {{\mathrm{\pi}} \mathord{\left/ {\vphantom {{\mathrm{\pi}} 4}} \right. } 4}$ and defining both parameters $\beta$ and $\gamma$ as variables, the designed diatomic metasurface can be employed to perform amplitude and phase modulation simultaneously. The complex amplitude modulation strategy, which possesses spin-selective properties, was evaluated using various parameter combinations selected sequentially at 22.5° intervals, as illustrated in Fig. 7(a). The results of the parameterized scans indicate that as parameter $\beta$ increases gradually from 0° to 180°, the amplitudes observed in the LCP→RCP channel, corresponding to various parameter values of $\gamma$, progressively decrease. In contrast, no discernible trend in the transmission amplitude is observed in the other three channels, highlighting the spin-selective nature of the process. Additionally, the phase delays in the LCP→LCP, RCP→RCP, LCP→RCP and RCP→RCP channels are presented in Fig. 7(b), where parameters $\beta$ and $\gamma$ are varied simultaneously. Notably, the discrete phase curves obtained from the LCP→RCP channel offer comprehensive coverage of the 2π profile.

Figure  7.  Full-Size Img PowerPoint

(a) Amplitude and (b) phase shift corresponding to spin-dependent pure amplitude modulation obtained by scanning the parameter factor β, including LCP→LCP, RCP→LCP, LCP→RCP and RCP→RCP channels. (c) Sample III and Sample IV obtained by utilizing the ICP etching technique. (d) Electric field distribution at the focal plane of the assembled meta-lens when β is equal to 0° and 90°, respectively, including simulation and experimental results. (e) Normalized amplitude profiles extracted at the focal plane along the x-direction, corresponding to Sample III and Sample IV.

Subsequently, various parameter combinations associated with $\beta$ and $\gamma$ were selected to evaluate the design strategy of THz meta-lenses, focusing on different intensities derived from both simulation and experiment results, respectively. Meta-molecules corresponding to γ = 0° and γ = 90°, were considered as candidates, and the desired meta-lens arrays were constructed by utilizing the spin-dependent geometrical phases. Additionally, silicon wafers with high resistivity and low absorption were processed using a standard ICP etching technique. SEM images of the samples designated as Sample III and Sample IV are presented in Fig. 7(c). The images reveal smooth surfaces and steep sidewalls, indicating acceptable fabrication tolerances. Figure 7(d) illustrates the electric field distribution in the focal plane, where two spots with markedly different intensity distributions are clearly observable at the center for angles γ of 0° and 90°, respectively. It is important to note that these measurements were obtained using the near-field THz detection system. The normalized amplitude distribution, extracted at the focal plane along the x-direction, is presented in Fig. 7(e), which includes both simulation and experimental results. The results obtained at this magnitude not only demonstrate the complex amplitude modulation properties of the metasurface but also reveal effective spin-dependent focusing effects. When integrated into the imaging system, the meta-lens can facilitate chiral detection.

Conclusions

In conclusion, we propose and develop a strategy for assembling diatomic metasurfaces grounded in the principle of multiple geometric phases. We select a pair of HWPs with an intrinsic phase difference of 90° as candidates for modulating the transmitted field by controlling their relative rotation angles. Each degree of freedom determined by the eigen-parameters is expressed through a stepwise superposition mechanism, which can be quantitatively represented by the Jones matrix. This design strategy facilitates rapid theoretical predictions of transmission fields with spin selectivity. To illustrate this concept, we present a series of examples involving spin-dependent metasurfaces. These include applications in THz holography (geometric phase modulation), broadband AT spectrum (pure phase modulation), THz near-field imaging (pure amplitude modulation), and the generation of controllable focusing fields (complex amplitude modulation). The experimental results agree well with the simulations, thus confirming the feasibility of the proposed strategy. The generalized diatomic metasurface mechanism offers potential applications in meta-optical based message encryption.