| Citation: | He C, Zhao D, Fan F et al. Pluggable multitask diffractive neural networks based on cascaded metasurfaces. Opto-Electron Adv 7, 230005 (2024). doi: 10.29026/oea.2024.230005 |
Pluggable multitask diffractive neural networks based on cascaded metasurfaces
-
Abstract
Optical neural networks have significant advantages in terms of power consumption, parallelism, and high computing speed, which has intrigued extensive attention in both academic and engineering communities. It has been considered as one of the powerful tools in promoting the fields of imaging processing and object recognition. However, the existing optical system architecture cannot be reconstructed to the realization of multi-functional artificial intelligence systems simultaneously. To push the development of this issue, we propose the pluggable diffractive neural networks (P-DNN), a general paradigm resorting to the cascaded metasurfaces, which can be applied to recognize various tasks by switching internal plug-ins. As the proof-of-principle, the recognition functions of six types of handwritten digits and six types of fashions are numerical simulated and experimental demonstrated at near-infrared regimes. Encouragingly, the proposed paradigm not only improves the flexibility of the optical neural networks but paves the new route for achieving high-speed, low-power and versatile artificial intelligence systems. -
-
References
[1] Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Commun ACM 60, 84–90 (2017). doi: 10.1145/3065386 [2] He KM, Zhang XY, Ren SQ, Sun J. Deep residual learning for image recognition. In Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition 770–778 (IEEE, 2016); http://doi.org/10.1109/CVPR.2016.90. [3] Zhou HQ, Wang YT, Li X, Xu ZT, Li XW et al. A deep learning approach for trustworthy high-fidelity computational holographic orbital angular momentum communication. Appl Phys Lett 119, 044104 (2021). doi: 10.1063/5.0051132 [4] Guo YM, Zhong LB, Min L, Wang JY, Wu Y et al. Adaptive optics based on machine learning: a review. Opto-Electron Adv 5, 200082 (2022). doi: 10.29026/oea.2022.200082 [5] Krasikov S, Tranter A, Bogdanov A, Kivshar Y. Intelligent metaphotonics empowered by machine learning. Opto-Electron Adv 5, 210147 (2022). doi: 10.29026/oea.2022.210147 [6] Sainath TN, Mohamed AR, Kingsbury B, Ramabhadran B. Deep convolutional neural networks for LVCSR. In Proceedings of 2013 IEEE International Conference on Acoustics, Speech and Signal Processing 8614–8618 (IEEE, 2013);http://doi.org/10.1109/ICASSP.2013.6639347. [7] Hinton G, Deng L, Yu D, Dahl GE, Mohamed AR et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process Mag 29, 82–97 (2012). doi: 10.1109/MSP.2012.2205597 [8] Collobert R, Weston J, Bottou L, Karlen M, Kavukcuoglu K et al. Natural language processing (almost) from scratch. J Mach Learn Res 12, 2493–2537 (2011). doi: 10.5555/1953048.2078186 [9] Markram H. The blue brain project. Nat Rev Neurosci 7, 153–160 (2006). doi: 10.1038/nrn1848 [10] Shen YC, Harris NC, Skirlo S, Prabhu M, Baehr-Jones T et al. Deep learning with coherent nanophotonic circuits. Nat Photonics 11, 441–446 (2017). doi: 10.1038/nphoton.2017.93 [11] Feldmann J, Youngblood N, Karpov M, Gehring H, Li X et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58 (2021). doi: 10.1038/s41586-020-03070-1 [12] Xu XY, Tan MX, Corcoran B, Wu JY, Boes A et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 589, 44–51 (2021). doi: 10.1038/s41586-020-03063-0 [13] Goi E, Chen X, Zhang QM, Cumming BP, Schoenhardt S et al. Nanoprinted high-neuron-density optical linear perceptrons performing near-infrared inference on a CMOS chip. Light Sci Appl 10, 40 (2021). doi: 10.1038/s41377-021-00483-z [14] Ashtiani F, Geers AJ, Aflatouni F. An on-chip photonic deep neural network for image classification. Nature 606, 501–506 (2022). doi: 10.1038/s41586-022-04714-0 [15] Zarei S, Marzban MR, Khavasi A. Integrated photonic neural network based on silicon metalines. Opt Express 28, 36668–36684 (2020). doi: 10.1364/OE.404386 [16] Chen H, Feng JN, Jiang MW, Wang YQ, Lin J et al. Diffractive deep neural networks at visible wavelengths. Engineering 7, 1483–1491 (2021). doi: 10.1016/j.eng.2020.07.032 [17] Liu J, Wu QH, Sui XB, Chen Q, Gu GH et al. Research progress in optical neural networks: theory, applications and developments. PhotoniX 2, 5 (2021). doi: 10.1186/s43074-021-00026-0 [18] Zhang X, Huang LL, Zhao RZ, Zhou HQ, Li X et al. Basis function approach for diffractive pattern generation with Dammann vortex metasurfaces. Sci Adv 8, eabp8073 (2022). doi: 10.1126/sciadv.abp8073 [19] Lin X, Rivenson Y, Yardimci NT, Veli M, Luo Y et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018). doi: 10.1126/science.aat8084 [20] Zhao RZ, Huang LL, Wang YT. Recent advances in multi-dimensional metasurfaces holographic technologies. PhotoniX 1, 20 (2020). doi: 10.1186/s43074-020-00020-y [21] Zhang YX, Pu MB, Jin JJ, Lu XJ, Guo YH et al. Crosstalk-free achromatic full Stokes imaging polarimetry metasurface enabled by polarization-dependent phase optimization. Opto-Electron Adv 5, 220058 (2022). doi: 10.29026/oea.2022.220058 [22] Badloe T, Lee S, Rho J. Computation at the speed of light: metamaterials for all-optical calculations and neural networks. Adv Photon 4, 064002 (2022). doi: 10.1117/1.AP.4.6.064002 [23] Veli M, Mengu D, Yardimci NT, Luo Y, Li JX et al. Terahertz pulse shaping using diffractive surfaces. Nat Commun 12, 37 (2021). doi: 10.1038/s41467-020-20268-z [24] Qian C, Lin X, Lin XB, Xu J, Sun Y et al. Performing optical logic operations by a diffractive neural network. Light Sci Appl 9, 59 (2020). doi: 10.1038/s41377-020-0303-2 [25] Wang PP, Xiong WJ, Huang ZB, He YL, Xie ZQ et al. Orbital angular momentum mode logical operation using optical diffractive neural network. Photon Res 9, 2116–2124 (2021). doi: 10.1364/PRJ.432919 [26] Huang ZB, He YL, Wang PP, Xiong WJ, Wu HS et al. Orbital angular momentum deep multiplexing holography via an optical diffractive neural network. Opt Express 30, 5569–5584 (2022). doi: 10.1364/OE.447337 [27] Rahman SS, Ozcan A. Computer-free, all-optical reconstruction of holograms using diffractive networks. ACS Photonics 8, 3375–3384 (2021). doi: 10.1021/acsphotonics.1c01365 [28] Mengu D, Ozcan A. All-optical phase recovery: diffractive computing for quantitative phase imaging. Adv Opt Mater 10, 2200281 (2022). doi: 10.1002/adom.202200281 [29] Li JX, Hung YC, Kulce O, Mengu D, Ozcan A. Polarization multiplexed diffractive computing: all-optical implementation of a group of linear transformations through a polarization-encoded diffractive network. Light Sci Appl 11, 153 (2022). doi: 10.1038/s41377-022-00849-x [30] Shi JS, Zhou L, Liu TG, Hu C, Liu KW et al. Multiple-view D2NNs array: realizing robust 3D object recognition. Opt Lett 46, 3388–3391 (2021). doi: 10.1364/OL.432309 [31] Rahman SS, Li JX, Mengu D, Rivenson Y, Ozcan A. Ensemble learning of diffractive optical networks. Light Sci Appl 10, 14 (2021). doi: 10.1038/s41377-020-00446-w [32] Yan T, Wu JM, Zhou TK, Xie H, Xu F et al. Fourier-space diffractive deep neural network. Phys Rev Lett 123, 023901 (2019). doi: 10.1103/PhysRevLett.123.023901 [33] Liu C, Ma Q, Luo ZJ, Hong QR, Xiao Q et al. A programmable diffractive deep neural network based on a digital-coding metasurface array. Nat Electron 5, 113–122 (2022). doi: 10.1038/s41928-022-00719-9 [34] Zhou TK, Lin X, Wu JM, Chen YT, Xie H et al. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat Photonics 15, 367–373 (2021). doi: 10.1038/s41566-021-00796-w [35] Li YJ, Chen RY, Sensale-Rodriguez B, Gao WL, Yu CX. Real-time multi-task diffractive deep neural networks via hardware-software co-design. Sci Rep 11, 11013 (2021). doi: 10.1038/s41598-021-90221-7 [36] Luo XH, Hu YQ, Ou XN, Li X, Lai JJ et al. Metasurface-enabled on-chip multiplexed diffractive neural networks in the visible. Light Sci Appl 11, 158 (2022). doi: 10.1038/s41377-022-00844-2 [37] Georgi P, Wei QS, Sain B, Schlickriede C, Wang YT et al. Optical secret sharing with cascaded metasurface holography. Sci Adv 7, eabf9718 (2021). doi: 10.1126/sciadv.abf9718 [38] Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE 86, 2278–2324 (1998). doi: 10.1109/5.726791 [39] Xiao H, Rasul K, Vollgraf R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv: 1708.07747 (2017). https://doi.org/10.48550/arXiv.1708.07747 [40] Goodman JW. Introduction to Fourier Optics and Holography 3rd ed (Roberts and Company, Englewood, 2005). [41] Mandel L, Wolf E. Some properties of coherent light. J Opt Soc Am 51, 815–819 (1961). doi: 10.1364/JOSA.51.000815 [42] Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett 96, 163905 (2006). doi: 10.1103/PhysRevLett.96.163905 -
Supplementary Information
Supplementary information for Pluggable multitask diffractive neural networks based on cascaded metasurfaces 
-
Access History
Article Metrics
-
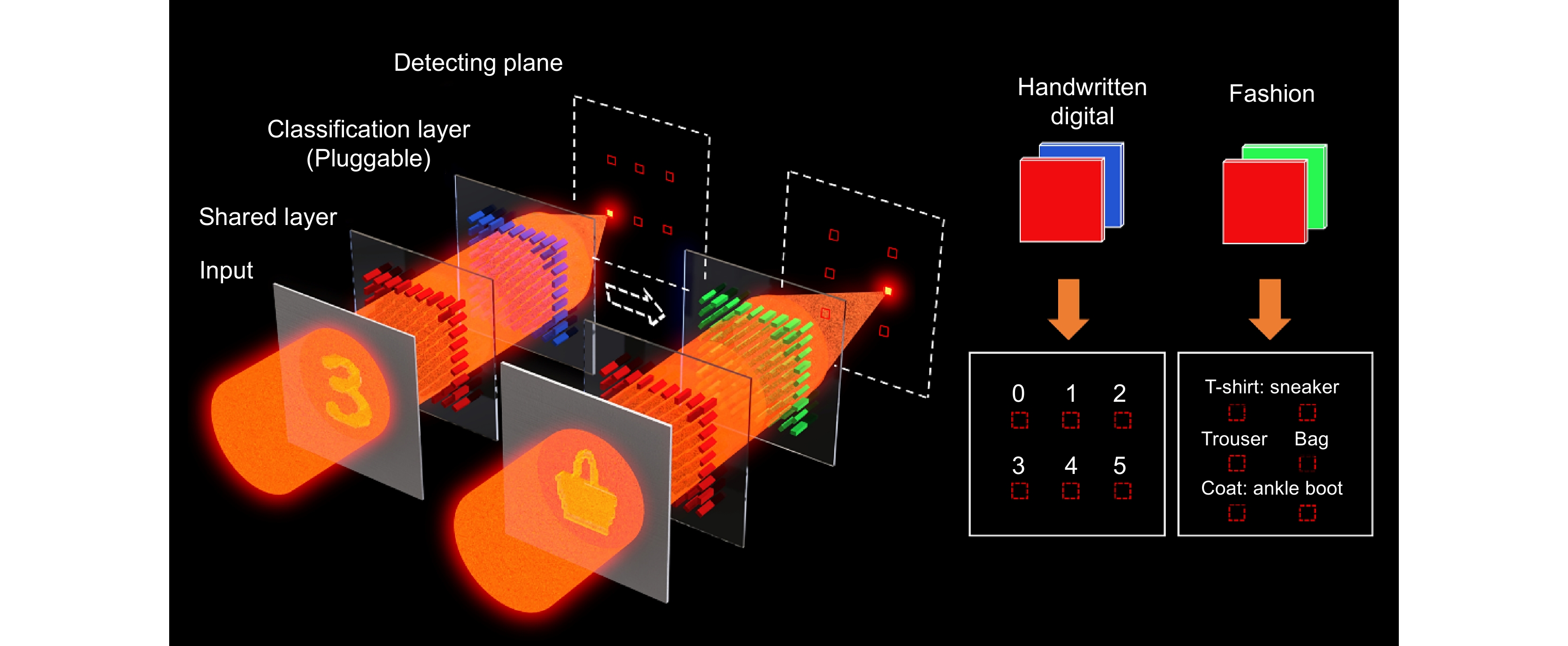
Figure 1.
Concept of pluggable diffractive neural networks (P-DNN) for multiple tasks. P-DNN is composed of common layers (marked in red) and classification layers (marked in blue and green, respectively). The recognition of handwritten digits and fashion datasets can be achieved by switching plugins of classification layers. When parallel light is encoded as a specific input and passed through a two-layer pluggable D2NN, the light can be focused on a specified region of the detection plane to achieve classification.
-
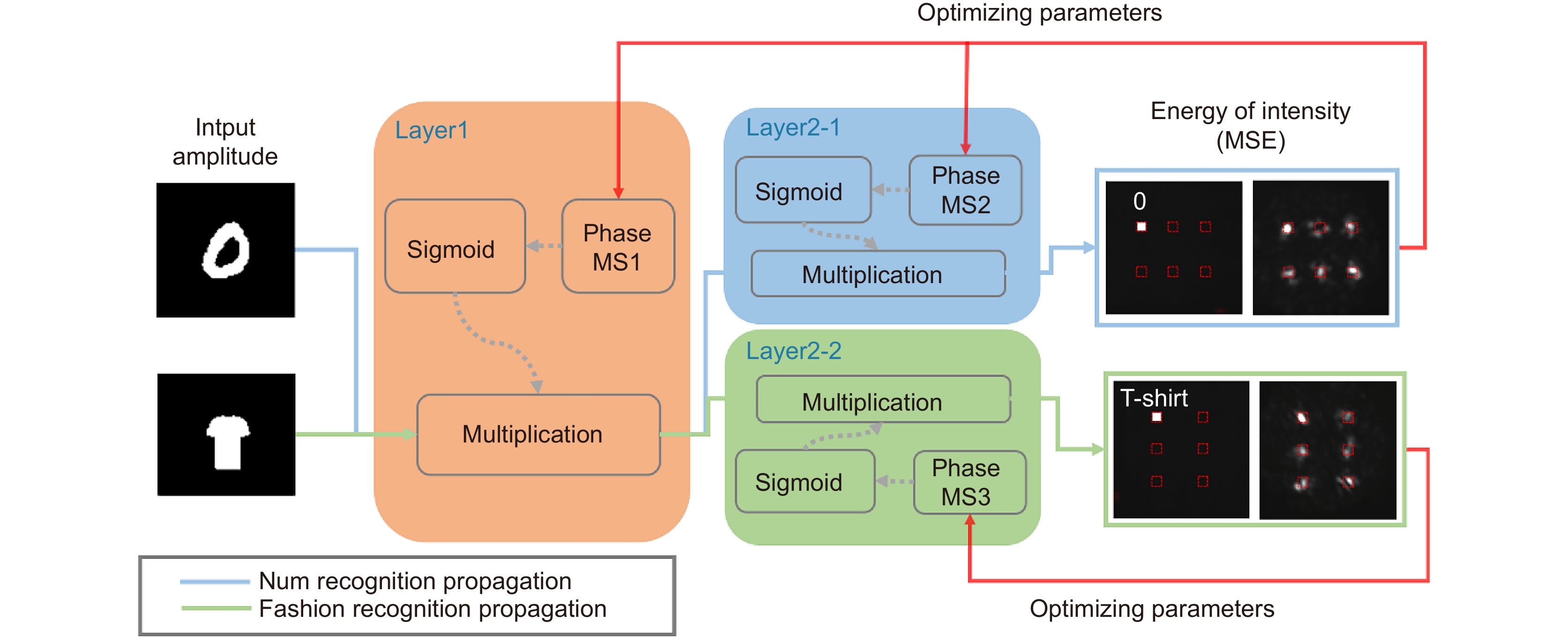
Figure 2.
Flowchart of multi-task P-DNN design. The information of the input object is encoded into the amplitude channel, which propagates in free space. The propagated complex field is multiplied by the phase at each layer before being passed to the next layer. The network parameters are optimized according to the mean square error (MSE) of the output field energy. The sigmoid function is used to constrain the phase of each neuron. In the first training, the parameters of the common layer and the classification layer need to be trained simultaneously. In the subsequent training of other tasks, only the parameters of the classification layer need to be optimized. MS: metasurface
-
Figure 3.
Design of the nanostructure based on geometric phase principle. (a) Schematic of an amorphous silicon nanorod fabricated on a glass substrate, where Px and Py are periods in the x and y directions, H is the height, and L and W are the length and width, respectively. (b) Amplitude map of the circular transmission coefficient in cross- and co-polarization for different geometry sizes. (c) Schematic diagram of the deflection angle of the nanofin. (d) Relationship between the rotation angle of the nanofin and the additional phase.
-
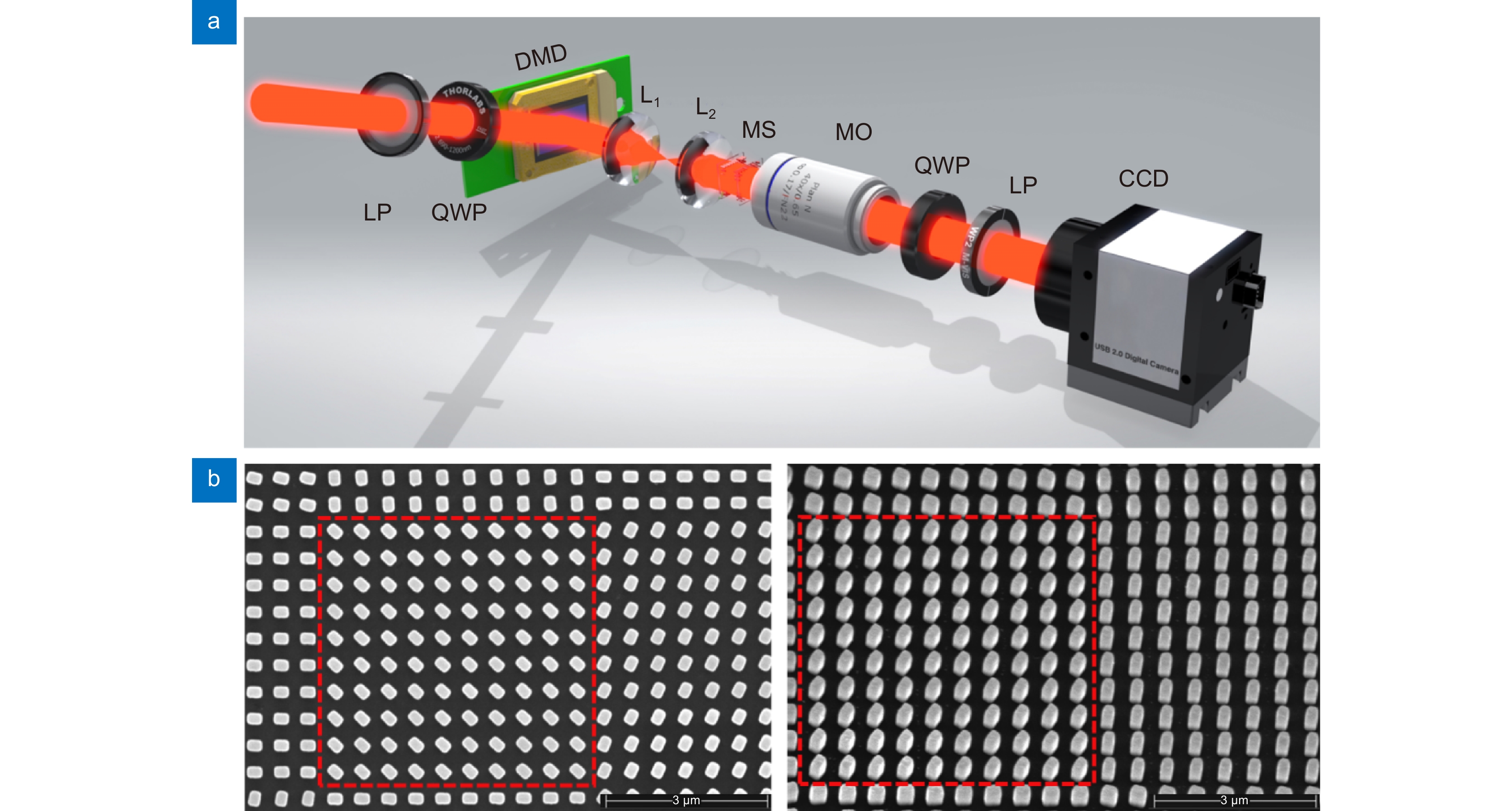
Figure 4.
Experimental setup and the SEM images of the metasurface. (a) Schematic of the experimental setup for observing the object classification. P: linear polarizer, QWP: quarter waveplate, MS: metasurface, MO: microscope objective. (b) The SEM images of the metasurface in the top and side view, respectively. A large pixel consisting of a 10 × 10 array of nanofins is marked by red dotted lines.
-
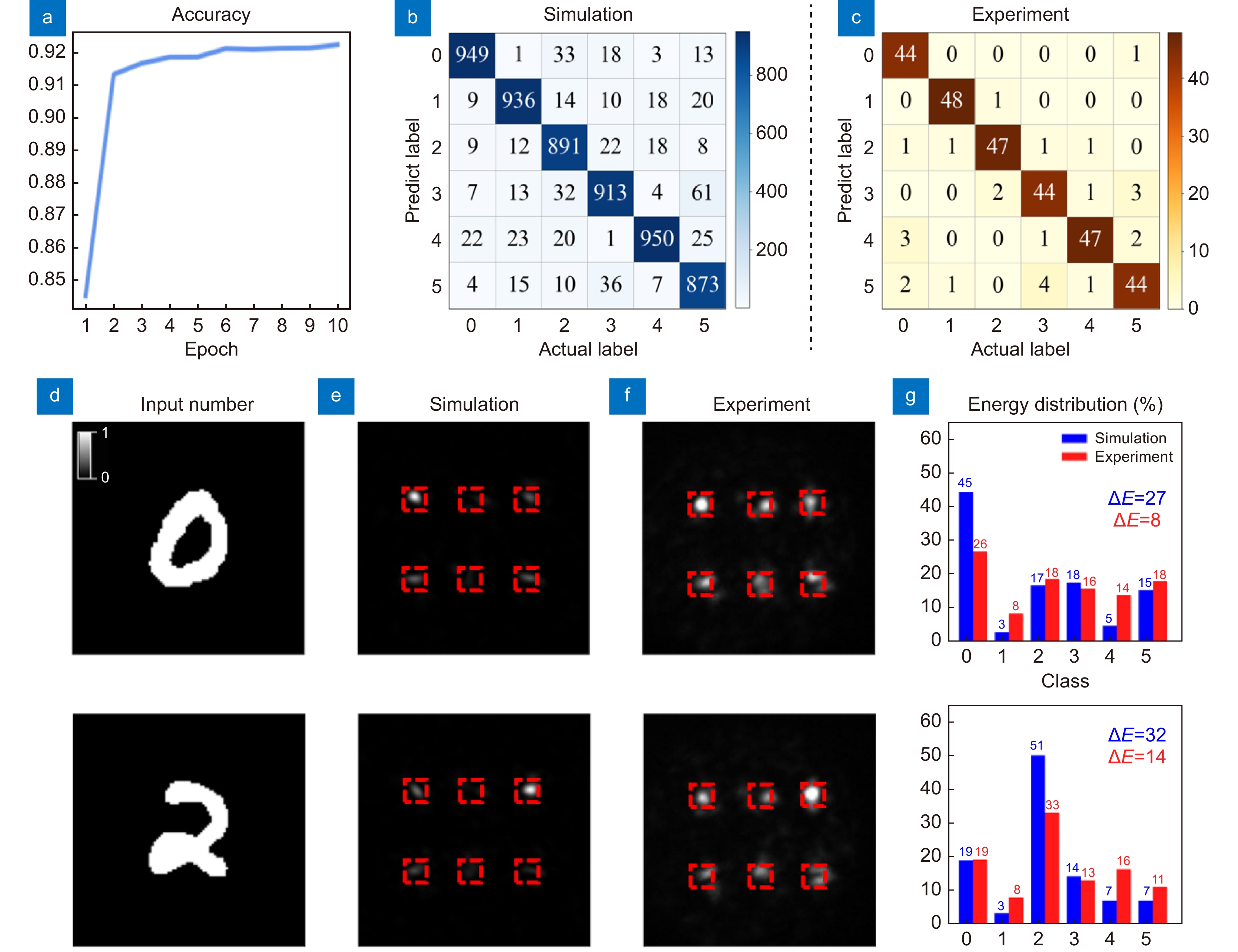
Figure 5.
Simulation and experiment result of num-P-DNN. (a) Training accuracy is 92% after training 10 epochs. (b, c) Simulation and experimental results of confusion matrix for handwritten digits. The Simulation and experimental results test accuracy is 91.8% and 91.3% respectively, which is obtained by dividing the sum of elements on the main diagonal of confusion matrix by the sum of all elements. (d) Handwritten digital input images were encoded into amplitude channel. (e, f) Output energy distribution maps of handwritten digits in simulations and experiments. (g) The energy distribution of handwritten digits experimental results and simulation results. ΔE represents the difference between the percentage of maximum and second maximum energy.
-
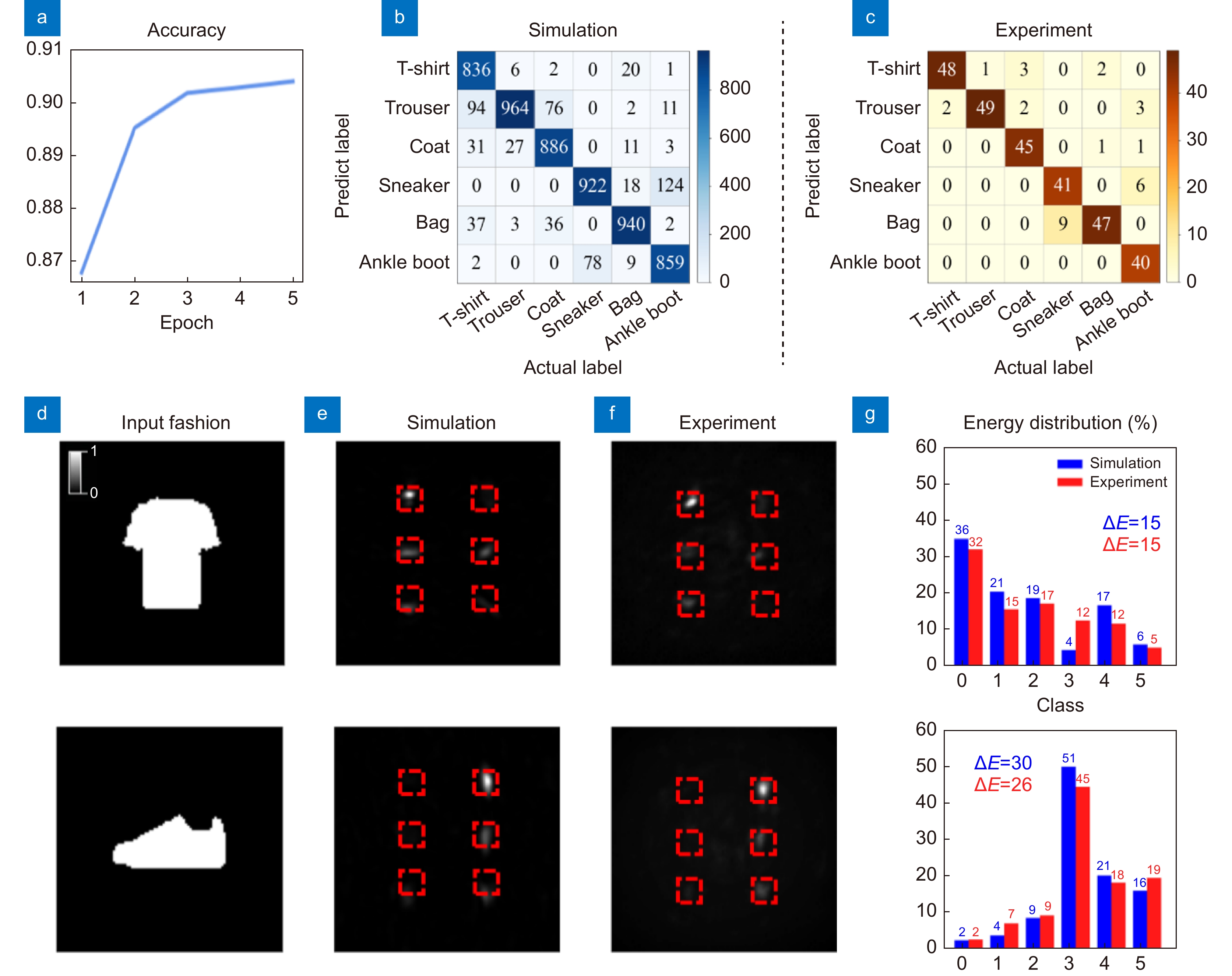
Figure 6.
Simulation and experiment result of fashion-P-DNN. (a) Training accuracy is 91% after training 5 epochs. (b, c) Simulation and experimental results of confusion matrix for fashions classification. The Simulation and experimental results test accuracy is 90.2% and 90% respectively, which is obtained by dividing the sum of elements on the main diagonal of confusion matrix by the sum of all elements. In the simulation and experimental results, the test accuracy reaches 90.2% and 90%, respectively. (d) Fashion input images were encoded into amplitude channel. (e, f) Output plane energy distribution maps of fashions in simulations and experiments. (g) Energy distribution percentage of experimental and simulated results of fashions. ΔE represents the difference between the percentage of maximum and second maximum energy.

 E-mail Alert
E-mail Alert RSS
RSS

 DownLoad:
DownLoad: