-
摘要
在基于图像传感器的倾斜镜控制系统中,由于传感器采样频率和系统延时的影响,限制了系统的闭环性能和控制带宽。在有限带宽的条件下,本文提出利用光栅尺测量位置,差分得到速度,实现基于图像传感器系统的速度-位置反馈控制,从而提升倾斜镜控制系统的误差抑制能力。速度反馈环节的引入,使控制系统呈微分特性,当速度反馈闭环完成后,图像位置回路具有积分特性,此时使用PI控制器稳定系统,从而使得系统从零型上升为二型系统,提升系统的误差抑制能力。仿真和实验都证明这种方法可以有效地提高跟踪控制系统的闭环性能。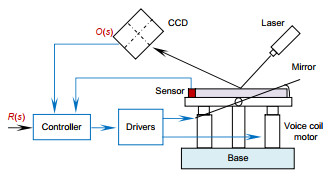
Abstract
In the image-based tip-tilt mirror control system, the closed-loop performance and bandwidth of the system and are limited due to the influence of sensor sampling frequency and system delay. Under the condition of limited bandwidth, this paper proposes to use linear encoder to measure the position, and get the rate signal by difference. The position-rate feedback control based on the image sensor system is realized to improve the error suppression ability of the tip-tilt mirror control system. Because of the addition of rate feedback, the control system has differential characteristics. When the rate feedback closed-loop is completed, the image position loop has integral characteristic. At this time, a PI controller is used to stabilize the system, which makes the system rise from zero type to two type system, and improves the error suppression ability of the system. Simulation and experiment show that this method can effectively improve the closed-loop performance of the tracking control system in low frequency domain.
-
1. 引言
倾斜镜控制系统广泛应用于光电跟踪系统中,在目标跟踪、目标观测、空间通信等领域中有着广泛的应用[1-3]。图像传感器探测目标,为控制系统提供位置偏差,该偏差为倾斜镜的输入信号,由此形成位置闭环系统。倾斜镜控制系统是实现光电跟踪系统高精度跟踪的关键,提高跟踪性能最有效的办法是在高带宽的条件下提高控制系统的增益。然而在基于图像的倾斜镜控制系统中,由于大量的时延以及图像传感器采样频率的限制,很难提升控制系统的带宽[4-5]。大量文献显示,对于基于图像的倾斜镜控制系统,研究者从硬件和软件方面分别提出了各种方法提高倾斜镜系统跟踪性能[6]。在硬件方面,有研究人员提出减少时间延迟、提高图像传感器的采样频率,然而一味的减少时延会影响图像传感器的成像[7];在软件方面,有学者提出使用加速度计或陀螺增加惯性传感器的方式使控制系统形成多闭环的控制模式[8-10],但是由于加速度计或陀螺安装方式为接触式安装,会增加倾斜镜的负载,从而影响系统响应。光栅尺[11-13]是一种非接触式传感器,其安装不会增加驱动负载,且具有高分辨率及精度,可以将所测量的位置量差分得到速率。本文提出一种基于光栅测量的倾斜镜位置速率控制方法,其原理是由光栅尺测量的倾斜量计算得到倾斜镜的倾斜速率,从而与采集目标位置的图像传感器实现速度-位置控制。
2. 倾斜镜控制系统
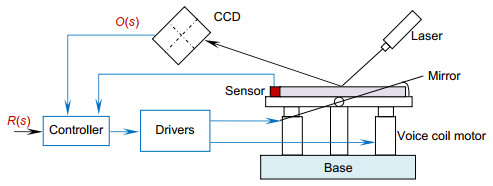
基于图像倾斜镜控制系统组成如图 1所示,包括倾斜镜、图像传感器、控制单元和驱动器。激光用于模拟空间中的运动目标。目标位置信息由CCD图像传感器提供。控制器用来实现控制算法。驱动器驱动音圈电机以实现倾斜镜的跟踪目标。倾斜镜的倾斜量由安装在倾斜镜上的传感器获得。
2.1 传统位置回路控制
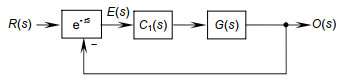
传统基于图像倾斜镜控制系统框图如图 2所示。其中,${{\rm{e}}^{ - \tau s}}$表示延迟特性,C(s)表示控制器,G(s)表示被控对象(倾斜镜、驱动),E(s)表示闭环误差。倾斜镜系统是零型系统,一般情况下G(s)的特性近似等于1。因此对于位置控制的控制系统可以理解为仅有延迟特性的控制系统,则开环传递函数:
式中:$\gamma $是相位裕度,${\omega _{\rm{c}}}$是截止频率;${K_{\rm{g}}}$是幅值裕度,${\omega _{\rm{g}}}$是穿越频率。控制器$C(s) = K/s$可以稳定该系统,由此根据式(2)满足相位裕度$\tau {\omega _{\rm{c}}} = {\rm{ \mathsf{ π} }}/4$,$K/{\omega _{\rm{c}}} = 1$,解得$K = {\omega _{\rm{c}}} = {\rm{ \mathsf{ π} }}/4\tau $,此时幅值裕度${K_{\rm{g}}}{\rm{ = }}6.0206 > 6$。控制器${C_1}(s) = {\rm{ \mathsf{ π} }}/4\tau s$,其参数取决于系统的延迟系数。由此系统的误差抑制函数:
式(3)给出的误差传递函数表明,系统的误差抑制能力会受到CCD时间延迟的限制。由于时间延迟的存在,较难提高控制系统的闭环带宽,因此本文提出一种在有限带宽的条件下,加入速度回路来提升系统对误差的抑制能力的方法。
闭环系统的稳定性与开环特性的幅值裕度(GM,用${K_{\rm{g}}}$表示)和相位裕度(PM,用$\gamma $表示)有关,通常需要满足${K_{\rm{g}}}$≥6 dB、$\gamma $≥π/4。本文选取$\gamma $=π/4,根据幅值裕度和相位裕度的定义得:
2.2 速率-位置回路控制
2.2.1 速度-位置控制模型
消除积分参数得:
令$\frac{{{\rm{d}}{K_{\rm{P}}}}}{{{\rm{d}}{{\omega '}_{\rm{c}}}}} = 0$,增益最大,得$\tau {\omega '_{\rm{c}}} \approx 0.5253$,求得${K_{\rm{P}}} = 0.07069/{\tau ^2}$,${K_{\rm{I}}} = 7.15326/\tau $。误差抑制传递函数:
取相位裕度$\gamma $=π/4,根据相位裕度的定义得:
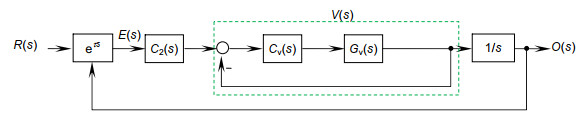
倾斜镜控制系统位置开环特性是一个零型系统,对误差抑制能力有限。为了进一步提高系统对误差的抑制能力,在有限带宽的条件下改变被控对象特性。在原有的位置回路引入速度回路,使系统开环特性在低频呈微分特性。速度控制回路的引入,将系统的型别由零型提升到Ⅰ型。倾斜镜的速率-位置回路控制框图如图 3所示。
相较于仅有位置回路的倾斜镜控制系统,速度回路的引入使得位置回路开环特性存在一阶积分环节。其中
表示速度回路的闭环传递函数。当速度回路完成闭环后V(s)≈1,对于具有积分特性的被控对象,PI(比例-积分)控制器可以稳定该系统,位置回路的开环传递函数:
和式(3)相比,两阶积分引入了控制系统。
2.2.2 光栅尺测速原理
光栅尺也称为光栅尺位移传感器(光栅尺传感器),是利用光栅的光学原理测量反馈装置。可用作直线位移或者角位移的检测。其测量输出的信号为数字脉冲,具有检测范围大,检测精度高,响应速度快的特点。本文所使用的光栅尺传感器为英国雷尼绍公司的直线绝对式光栅尺[11],其安装方式为非接触式安装。将光栅尺所测得的位置信息进行差分得到速度,其测速原理如下:
其传递函数如下:
幅频和相频特性为
由拉氏变换可得传递函数如下:
式中:$p(k + 1)$,$p(k)$为相邻采样时刻的位置信号;ΔT为采样周期,由系统的采样频率所决定。将式(8)进行z变换可得:
根据式(12)可知,想要实现控制系统对目标的快速跟踪,需要系统的采样频率很高;采样频率越高, 系统的带宽就越宽,本文中对光栅尺数据采集率为5 kHz。
2.2.3 性能对比
令$20\lg \left| {{E_{\rm{p}}}/{E_{\rm{v}}}} \right|{\rm{ = }}0$,解得$\omega = 0.1189/\tau $,此时两种控制方法具有相同的误差抑制能力;当$\omega < 0.1189/\tau $,$20\lg \left| {{E_1}/{E_2}} \right| > 0$,此时说明速度-位置控制模式拥有更好的误差抑制能力;当$0.1189/\tau < \omega < {\rm{ \mathsf{ π} }}/4\tau $,显然$ - 5\;{\rm{dB}} < 20\lg \left| {{E_1}/{E_2}} \right| < 0$,此时位置回路控制模式误差抑制能力略优于速度-位置控制模式。总体上来讲,速度-位置控制模式拥有更好的误差抑制能力。
系统的误差抑制能力是评价闭环控制系统性能的一个关键参数。由式(3)、式(12)可得:
3. 实验验证
倾斜镜是一个对称的双轴系统,因此本实验只验证一个轴。基于图像的倾斜镜控制系统实验装置由倾斜镜、激光光源、反射镜、控制单元、驱动器和位置敏感探测器(PSD)等组成(如图 4所示)。在现有的实验室设备中,采用PSD来模拟具有200 Hz采样频率的CCD,延迟参数约为0.006 s,约为采样间隔0.002 s的三倍。安装在倾斜镜(图 3(b))上的光栅尺,其分辨率为50 nm。
3.1 闭环带宽对比
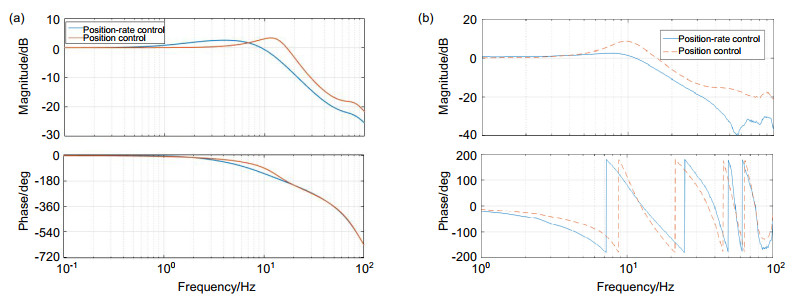
两种控制模式的闭环幅频响应图如图 5所示。
从图中得知当幅值达到-3 dB时,采用速度-位置回路的跟踪控制系统的频率略低于采用位置回路的跟踪控制系统。这表明采用速率反馈的控制系统闭环带宽较低,对控制带宽提升起不到明显的作用。但是因为速率控制回路的引入主要改善低频段的误差抑制能力,所以对本文结果没有影响。
3.2 误差抑制能力对比
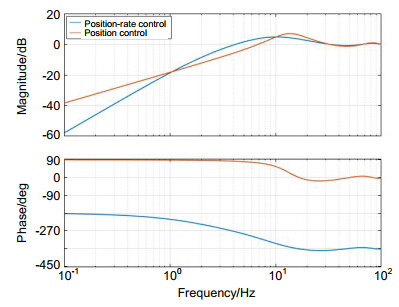
当频率小于1 Hz时,位置回路控制的误差抑制能力比速度-位置回路控制差。相反,当频率为1 Hz到7 Hz范围内时,位置回路误差抑制能力略优于速度-位置回路。速度-位置控制方法在中频范围内损失了一点误差抑制能力。结果表明,在低频范围内,基于图像的倾斜镜跟踪控制系统采用速度-位置回路控制的比仅采用位置回路控制具有更好的误差抑制能力。
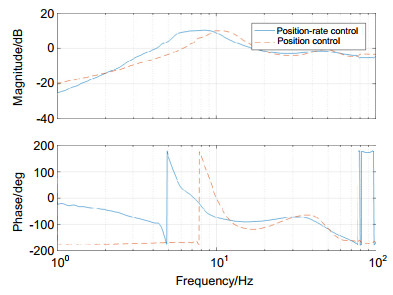
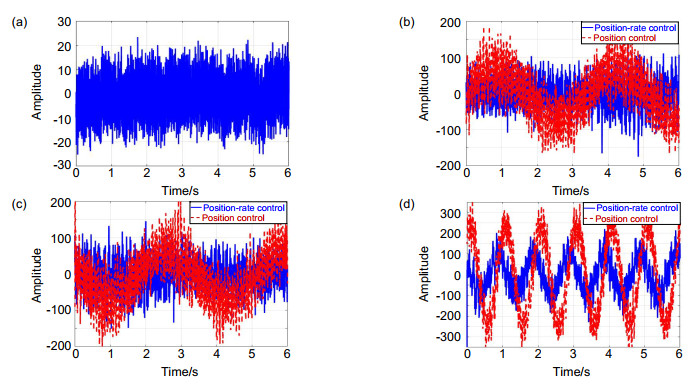
两种控制模式的误差抑制能力实验结果如图 7所示。实验结果表明,速度-位置控制模式下的误差抑制带宽(约4 Hz)低于位置控制模式下的误差衰减带宽(约6 Hz)。在2 Hz~6 Hz的频率范围内,位置控制方式的误差衰减性能稍好。在1 Hz~2 Hz左右的低频范围内,速度-位置控制方式比单位置控制方式有更好的误差抑制能力。虽然实验结果与理论分析不完全吻合,但变化趋势与仿真结果一致。此外,对2 Hz以下的频率进行了实验测试,使用的输入信号频率分别为0.1 Hz、0.3 Hz和1 Hz的正弦信号。实验结果的跟踪误差和PSD噪声如图 8所示。
图 6给出了式(3)和式(13)中描绘的两个误差传递函数的Bode响应。
实验中由于PSD噪声影响,误差衰减性能比仿真分析的结果差。当频率为0.1 Hz时,误差能力已达到极限。在低频范围内,采用速度-位置回路的控制方式比采用位置回路控制方式具有更好误差抑制能力。
4. 结论
为了提高倾斜镜系统的跟踪性能,提出了位置-速率控制。根据光栅尺的实际应用,讨论了倾斜镜的控制方式和光栅尺测速原理。从闭环稳定性和误差抑制两方面给出了倾斜镜系统实现速率反馈的条件。实验结果表明,该位置-速率控制方法能有效地提高闭环系统在低频的误差抑制能力。本研究未考虑外界干扰的影响。在今后的工作中,应集中考虑外界干扰的影响,需要考虑适当的方法抑制扰动,提高跟踪性能。前馈控制是一种很好的控制方法,这将是我们下一步的工作。
-
参考文献
Cochran R W, Vassar R H. Fast-steering mirrors in optical control systems[J]. Proceedings of SPIE, 1990, 1303: 245-251.
DOI: 10.1117/12.21507黄林海, 凡木文, 周睿, 等.大口径压电倾斜镜模型辨识与控制[J].光电工程, 2018, 45(3): 170704.
DOI: 10.12086/oee.2018.170704Huang L H, Fan M W, Zhou R, et al. System identification and control for large aperture fast-steering mirror driven by PZT[J]. Opto-Electronic Engineering, 2018, 45(3): 170704.
DOI: 10.12086/oee.2018.170704姜文汉.自适应光学发展综述[J].光电工程, 2018, 45(3): 170489.
DOI: 10.12086/oee.2018.170489Jiang W H. Overview of adaptive optics development[J]. Opto-Electronic Engineering, 2018, 45(3): 170489.
DOI: 10.12086/oee.2018.170489Gaffard J P, Boyer C. Adaptive optics: effect of sampling rate and time lags on the closed-loop bandwidth[J]. Proceedings of SPIE, 1990, 1237: 376-393.
DOI: 10.1117/12.19311展开 -
期刊类型引用(4)
-
版权信息
版权属于中国科学院光电技术研究所,但文章内容可以在本网站免费下载,以及免费用于学习和科研工作 -
关于本文
引用本文
Citation:阮勇, 徐田荣, 杨涛, 唐涛. 具有延迟特性的倾斜镜系统中速度-位置控制方法[J]. 光电工程, 2020, 47(12): 200006. DOI: 10.12086/oee.2020.200006Citation:Ruan Yong, Xu Tianrong, Yang Tao, Tang Tao. Position-rate control for the time delay control system of tip-tilt mirror. Opto-Electronic Engineering 47, 200006 (2020). DOI: 10.12086/oee.2020.200006导出引用出版历程
- 收稿日期 2020-01-02
- 修回日期 2020-02-11
- 刊出日期 2020-12-14
文章计量
访问数(6057) PDF下载数(907)
科研论文
具有延迟特性的倾斜镜系统中速度-位置控制方法
作者信息+
-
1.
中国科学院光电技术研究所,四川 成都 610209
-
2.
中国科学院光束控制重点实验室,四川 成都 610209
-
3.
中国科学院大学,北京 100049
Position-rate control for the time delay control system of tip-tilt mirror
- Ruan Yong1,2,3, ,
- Xu Tianrong1,2,3,
- Yang Tao1,2,3,
- Tang Tao1,2,3, ,
Author Information+
-
1.
Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China
-
2.
Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China
-
3.
University of Chinese Academy of Sciences, Beijing 100049, China
出版历程
DOI: 10.12086/oee.2020.200006
- 收稿日期: 2020-01-02
- 修回日期: 2020-02-11
- 刊出日期: 2020-12-14
- 6057 访问数
- 907 下载数
- 6 引用数


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载:

 本站查看
本站查看




