Advanced biological imaging techniques based on metasurfaces

Yongjae Jo; Hyemi Park; Hyeyoung Yoon; Inki Kim

doi:10.29026/oea.2024.240122

Abstract

Advanced imaging techniques have been widely used in various biological studies. Currently, numerous imaging modalities are utilized in biological applications, including medical imaging, diagnosis, biometrics, and fundamental biological research. Consequently, the demand for faster, clearer, and more accurate imaging techniques to support sophisticated biological studies has increased. However, there is a limitation in enhancing performance of imaging devices owing to the system complexity associated with bulky conventional optical elements. To address this issue, metasurfaces, which are flat and compact optical elements, have been considered potential candidates for biological imaging. Here, we comprehensively discuss the metasurface empowered various imaging applications in biology, including their working principles and design strategies. Furthermore, we compared conventional imaging modalities with the metasurface-based imaging system. Finally, we discuss the current challenges and offer future perspectives on metasurfaces.

Keywords

FullText(HTML)

Introduction

Metasurfaces, consisting of regularly aligned nanostructures, are considered promising optical components for imaging techniques. They can manipulate optical properties such as amplitude, phase, polarization, absorption, and reflection through the arrangement of subwavelength-sized meta-atoms²⁻⁶. Owing to their advantages over traditional refractive lenses, metasurfaces are characterized by their flatness, ultrathin profile, capability to achieve a high numerical aperture (NA), and versatility⁷⁻⁹. Metasurfaces are suitable for portable or miniaturized imaging devices that facilitate onsite diagnostics due to their flat profile and versatility^10,11. Additionally, they are capable of correcting aberrations to deliver clearer images^12,13. Recent studies focused on harnessing the benefits of metasurfaces for bioimaging applications. In this paper, we discuss the operating mechanisms, design principles, and wide applications of metasurfaces in bioimaging research. We first categorized bioimaging applications of metasurface into broad classes based on the subject, such as cell, animal and human imaging. Then, representative techniques are classified into more detailed subgroups based on the imaging modalities, such as super-resolution, analog image processing, fluorescent imaging, photoacoustic imaging, medical imaging and biometrics [Fig. 1]¹⁴⁻²⁸. For readability, we referred to metalenses, and other similar devices as the more general term “metasurfaces” since we comprehensively discuss the bioimaging techniques.

Biological imaging techniques are indispensable for the exploration of biological processes, structures, and states. Advanced imaging techniques have been widely studied for various biological applications, such as diagnosis, biometrics, and fundamental biological research. As the importance of biological imaging has been highlighted, there has been an increased demand for advanced imaging techniques that are faster, wider, clearer, and more accurate. However, enhanced performance is inevitably accompanied by increased system complexity, resulting in limited system performance. Many efforts have been made to reduce the system complexity by utilizing versatile and compact components that serve multiple functions, thereby creating a compressed optical system¹. Conventional optical elements encounter limitations in miniaturization beyond a certain thickness because of the limited refractive indices of natural materials². Furthermore, correcting aberrations often necessitates a combination of multiple lenses, resulting in an increased size and the need for precise alignment.

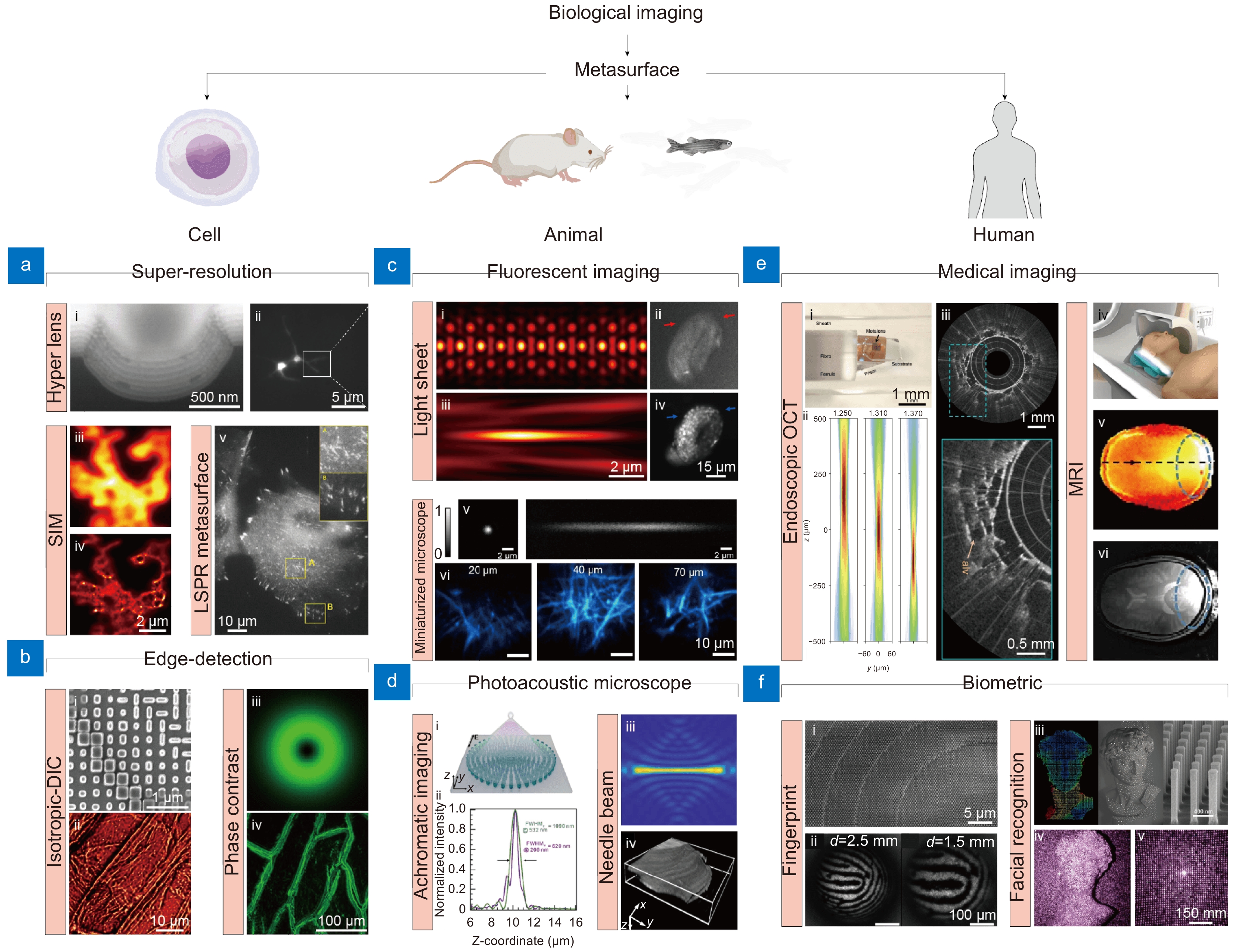
$Figure 1. Representative metasurface-based bioimaging techniques for cell, animal, and human applications. (a, b) Metasurface-based (a) super-resolution and (b) edge-detection imaging for cell imaging applications. (a-i) Cross-section of hyperlens and (a-ii) neuronal super-resolution image using hyperlens. (a-iii) Diffraction-limited and (a-iv) super-resolution image of same cells using metasurface-assisted SIM, respectively. (a-v) LSPR imaging of live cell. (b-i) SEM image of edge-detection metasurface and (b-ii) i-DIC image of onion epidermal cell. (b-iii) PSF of spiral phase metasurface and (b-iv) edge-enhanced image of onion epidermal cells. (c, d) Metasurface-based (c) fluorescent and PAM for (d) animal imaging. (c i-iv) PSF of lattice light sheet microscope in (c-i) XY and (c-iii) XZ plane and in vivo fluorescent image of developing embryos obtained by (c-ii) wide field and (c-iv) light sheet microscope. (c-v) PSF of metasurface-based miniaturized two-photon microscope and (c-vi) fluorescent image of Thy1-YFP mouse brain at different depth. (d) Metasurface-based PSF engineering for PAM applications. (d-i, d-ii) Schematic and intensity profile of an achromatic metasurface for dual-channel PAM. (d-iii) Needle beam PSF and (d-iv) label-free histological PAM image. (e, f) Metasurface-based (e) medical imaging and (f) biometric devices. (e-i) Optical setup and (e-ii) PSF of metasurface-based endoscopic OCT system. (e-iii) Human lung images. (e iv-vi) Metasurface-assisted MRI images. (f-i) SEM image of metasurface and (f-ii) fingerprint image obtained. (f-iii) Illustration of metasurface-based point cloud generation and (f-iv, f-v) implementation of 3D facial recognition. Figure reproduced with permission from: (a) (i) ref.14, Springer Nature; (ii) ref.15 American Chemical Society; (iii, iv) ref.16, Springer Nature; (v) ref.17, American Chemical Society; (b) (i, ii) ref.18, American Chemical Society; (iii, iv) ref.19 Springer Nature; (c) (i-iii) ref.20, De Gruyter; (ii-iv) ref.21, De Gruyter; (v, vi) ref.22, American Chemical Society; (d) (i, ii) ref.23, Elsevier; (iii, iv) ref.24, Elsevier; (e) (i, iii) ref.25, Springer Nature; (iv, vi) ref.26, Springer Nature; (f) (i, ii) ref.27, American Chemical Society; (iii-v) ref.28, American Chemical Society.$

Figure 1. Full-Size Img PowerPoint

Representative metasurface-based bioimaging techniques for cell, animal, and human applications. (a, b) Metasurface-based (a) super-resolution and (b) edge-detection imaging for cell imaging applications. (a-i) Cross-section of hyperlens and (a-ii) neuronal super-resolution image using hyperlens. (a-iii) Diffraction-limited and (a-iv) super-resolution image of same cells using metasurface-assisted SIM, respectively. (a-v) LSPR imaging of live cell. (b-i) SEM image of edge-detection metasurface and (b-ii) i-DIC image of onion epidermal cell. (b-iii) PSF of spiral phase metasurface and (b-iv) edge-enhanced image of onion epidermal cells. (c, d) Metasurface-based (c) fluorescent and PAM for (d) animal imaging. (c i-iv) PSF of lattice light sheet microscope in (c-i) XY and (c-iii) XZ plane and in vivo fluorescent image of developing embryos obtained by (c-ii) wide field and (c-iv) light sheet microscope. (c-v) PSF of metasurface-based miniaturized two-photon microscope and (c-vi) fluorescent image of Thy1-YFP mouse brain at different depth. (d) Metasurface-based PSF engineering for PAM applications. (d-i, d-ii) Schematic and intensity profile of an achromatic metasurface for dual-channel PAM. (d-iii) Needle beam PSF and (d-iv) label-free histological PAM image. (e, f) Metasurface-based (e) medical imaging and (f) biometric devices. (e-i) Optical setup and (e-ii) PSF of metasurface-based endoscopic OCT system. (e-iii) Human lung images. (e iv-vi) Metasurface-assisted MRI images. (f-i) SEM image of metasurface and (f-ii) fingerprint image obtained. (f-iii) Illustration of metasurface-based point cloud generation and (f-iv, f-v) implementation of 3D facial recognition. Figure reproduced with permission from: (a) (i) ref.¹⁴, Springer Nature; (ii) ref.¹⁵ American Chemical Society; (iii, iv) ref.¹⁶, Springer Nature; (v) ref.¹⁷, American Chemical Society; (b) (i, ii) ref.¹⁸, American Chemical Society; (iii, iv) ref.¹⁹ Springer Nature; (c) (i-iii) ref.²⁰, De Gruyter; (ii-iv) ref.²¹, De Gruyter; (v, vi) ref.²², American Chemical Society; (d) (i, ii) ref.²³, Elsevier; (iii, iv) ref.²⁴, Elsevier; (e) (i, iii) ref.²⁵, Springer Nature; (iv, vi) ref.²⁶, Springer Nature; (f) (i, ii) ref.²⁷, American Chemical Society; (iii-v) ref.²⁸, American Chemical Society.

Principle of electromagnetic phase modulation

To precisely refract the light path, it is necessary to carefully design the phase delay and transmission at each position on the metasurface. Designing a complex phase map capable of modulating light in the desired direction and intensity according to the generalized Snell’s law and diffraction optical theory enables the realization of diverse optical functionalities. In this section, we focus on the principles and design strategies for metasurfaces.

$\left\{\begin{array}{c}{{n}}_{\mathrm{t}}\mathrm{sin}\left({\theta }_{{\mathrm{t}}}\right)-{n}_{{\mathrm{i}}}\mathrm{sin}\left({\theta }_{{\mathrm{i}}}\right)=\dfrac{1}{{k}_{0}}\dfrac{{\mathrm{d}}{\Phi }}{{\mathrm{d}}x}\\ {{n}}_{\mathrm{i}}\mathrm{sin}\left({\theta }_{{\mathrm{r}}}\right)-{n}_{{\mathrm{i}}}\mathrm{sin}\left({\theta }_{{\mathrm{i}}}\right)=\dfrac{1}{{k}_{0}}\dfrac{{\mathrm{d}}{\Phi }}{{\mathrm{d}}x}\end{array}\right.\;.$

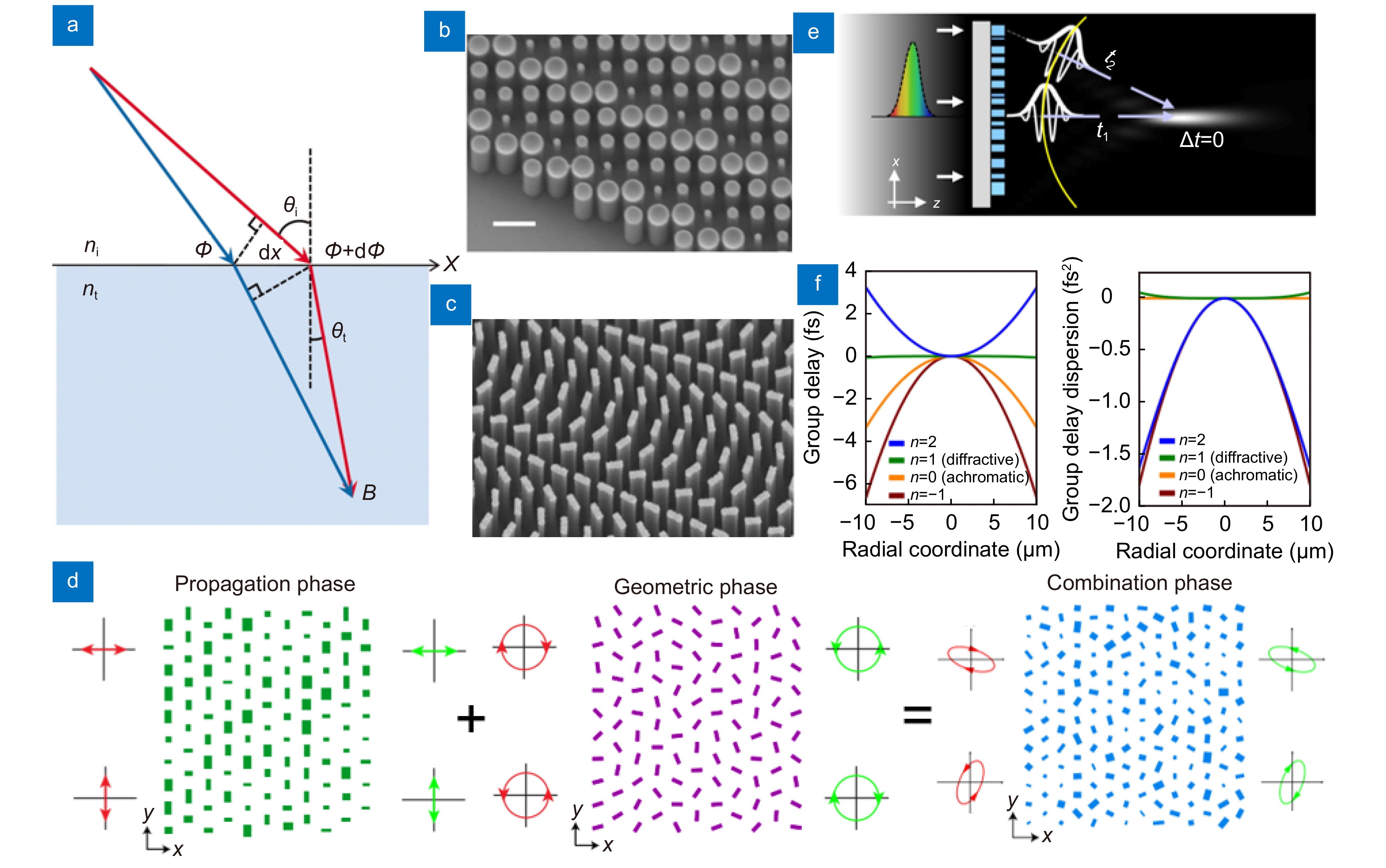
$Figure 2. Working principles of phase modulation of metasurface. (a) Schematic of the generalized Snell's law of refraction. The phase gradient causes additional refraction of light. (b) SEM image of the circular meta-atoms of propagation phase metasurface. (c) SEM image of the rectangular meta-atoms on geometric phase metasurface. (d) Schematic illustrating the principle of combining propagation and geometric phases. (e) An illustration depicting the spectral dispersion of metasurface in terms of group delay. (f) For a metasurface with a 530 nm wavelength and a 49 μm focal length, the group delay and group dispersion delay profiles are shown. Based on the value of n, the design can be optimized for achromatic or chromatic performance. Figure reproduced with permission from: (a) ref.29, American Association for the Advancement of Science; (b) ref.32, American Chemical Society; (c) ref.33, American Chemical Society; (d) adapted with permission from ref. 34, copyrighted by the American Physical Society; (e, f) ref.12, Springer Nature.$

Figure 2. Full-Size Img PowerPoint

Working principles of phase modulation of metasurface. (a) Schematic of the generalized Snell's law of refraction. The phase gradient causes additional refraction of light. (b) SEM image of the circular meta-atoms of propagation phase metasurface. (c) SEM image of the rectangular meta-atoms on geometric phase metasurface. (d) Schematic illustrating the principle of combining propagation and geometric phases. (e) An illustration depicting the spectral dispersion of metasurface in terms of group delay. (f) For a metasurface with a 530 nm wavelength and a 49 μm focal length, the group delay and group dispersion delay profiles are shown. Based on the value of n, the design can be optimized for achromatic or chromatic performance. Figure reproduced with permission from: (a) ref.²⁹, American Association for the Advancement of Science; (b) ref.³², American Chemical Society; (c) ref.³³, American Chemical Society; (d) adapted with permission from ref. ³⁴, copyrighted by the American Physical Society; (e, f) ref.¹², Springer Nature.

The operating principle of a metasurface follows the generalized Snell's law , which is essential for understanding how a metasurface controls the light path²⁹. In , ${n}_{\mathrm{i}}$ , ${n}_{\mathrm{t}}$ denote the refractive indices for the incident and transmission media respectively, while ${θ}_{\mathrm{i}}$ , ${θ}_{\mathrm{r}}$ , and ${θ}_{\mathrm{t}}$ correspond to the angles of incidence, reflection, and transmission at the interface []²⁹. The ${k}_{0}$ denotes the magnitude of the free-space wave vector, which can be expressed as ${2\mathrm{\pi }/{λ}}_{0}$ , where ${λ}_{0}$ is wavelength of free space. ${\rm{d}}{\Phi }/{\rm{d}}x$ represents the gradient of phase discontinuity. According to the generalized Snell's law, the light refraction path can be controlled by the phase gradient introduced on the metasurface. This principle allows metasurfaces to perform various optical functions, such as focusing or dispersing light, unlike conventional lenses^30,31.

Propagation phase

Propagation phase metasurfaces can be classified into two theories: nano waveguides and medium equivalent refractive index. The approach based on the medium equivalent refractive index utilizes the variation in refractive index between two or more media, where typically one of the media is a high refractive index material. It is the same concept as the generally known effective refractive index, which explains the complex structure of the meta-atom as an effective medium. It refers to the effective refractive index that appears when a wave propagates through the composite structure, allowing control of the phase change of light propagated through the meta-atom. This is used to describe the property of the meta-atom acting as an effective medium. Propagation phase modulation involves using meta-atoms as nano waveguides, where the phase delay is influenced by the effective refractive index and the dimensions of the meta-atom. More detailed discussion on how it acts as a waveguide will be covered in a sub-section, the dielectric material part.

The relationship between the incident and transmitted electric fields can be expressed using the Jones matrix [Eqs. (2, 3)]^35,36, which provides a mathematical framework for analyzing the effect of the metasurface on the polarization state of the incident light. The Jones matrix representation is given as below.

Propagation phase modulation is an innovative method for manipulating the phase delay of electromagnetic waves propagating through meta-atoms. The propagation phase is the phase accumulated during the propagation of light within the material of the meta-atom, which depends on the physical parameters of the material and the wavelength. By altering the physical structure of the meta-atom, it is possible to control the 2π phase for the incident polarized light. The physical structure here refers to the shape or physical dimensions of the meta-atom (such as height, length, width).

${{\boldsymbol{T}}}=\left[\begin{array}{cc}{T}_{xx}& {T}_{xy}\\ {T}_{yx}& {T}_{yy}\end{array}\right]\;,$

where $\boldsymbol{T}$ , ${\boldsymbol{E}}_{\rm{i}}$ and ${\boldsymbol{E}}_{\rm{t}}$ represents the transmission matrix, incident and transmitted electric field, respectively. In the context of propagation phase modulation, the transmission matrix $\boldsymbol{T}$ encapsulates the effect of the meta-atom's physical structure on the phase and amplitude of the transmitted light. By designing the elements of the transmission matrix, precise control over the phase shift, enabling advanced applications^12,37 like full-color imaging and high-resolution optical devices.

${{{\boldsymbol{E}}}}_{\mathrm{t}}={\boldsymbol{T{E}}}_{\rm{i}} \;,$

Geometric phase

The Jones matrix of rotated meta-atom can be expressed using the rotation matrix $\hat{{\boldsymbol{R}}}\left(\theta \right)$ []⁴⁰. Here, θ represents the rotation angle of the meta-atom. The rotation matrix $\hat{{\boldsymbol{R}}}\left(\theta \right)$ describes the rotation of the coordinate system by the angle $\theta$ . The rotation matrix and its inverse convert the transmission matrix ${\boldsymbol{T}}$ into ${\boldsymbol{T}}\left(\theta \right)$ to account for the rotated meta-atom.

${\boldsymbol{T}}\left(\theta \right)={\hat{{\boldsymbol{R}}}}^{-1}\left(\theta \right){\boldsymbol{T}}\hat{{\boldsymbol{R}}}\left(\theta \right) \;,$

Scanning electron microscopy (SEM) images of the meta-atoms in the propagation and geometric phases are shown in Fig. 2(b, c). The propagation and geometric phase are manipulated by varying the diameter of cylindrical meta-atoms [Fig. 2(b)] and rotating the meta-atoms [Fig. 2(c)], respectively. Intriguingly, the geometric phase can be combined with the propagation phase [Fig. 2(d)] to utilize the metasurface as a mode-changing (or multifunctional) optical component that operates differently depending on the polarization. This allows the metasurface to function as various optical elements and significantly expands the scope of metasurface optics.

${{\boldsymbol{T}}}^{{\rm{ circ}}}={\hat{{\boldsymbol{A}}}}^{-1}{\boldsymbol{T}}\left(\theta \right)\hat{{\boldsymbol{A}}}=\left[\begin{array}{cc}{{\boldsymbol{T}}}_{{\mathrm{RR}}}& {{\boldsymbol{T}}}_{{\mathrm{RL}}}\\ {{\boldsymbol{T}}}_{{\mathrm{LR}}}& {{\boldsymbol{T}}}_{{\mathrm{LL}}}\end{array}\right] \;,$

Geometric phase metasurfaces effectively utilize their degrees of freedom to manipulate various electromagnetic events, including unusual refraction or diffraction^3,41, holographic imaging⁴²⁻⁴⁴, and specialized beam generation^45,46. Moreover, some metasurfaces can induce complex geometric phases by utilizing meta-atoms with high-order rotational symmetry along with nonlinear and nonlocal responses, which are attributable to quasi-bound states in the continuum (quasi-BICs)^47,48. This has significantly expanded the range of optical functionalities that metasurfaces can offer, opening new possibilities for various optical applications through advancements in metasurface technology.

Practically, designing a metasurface using linearly polarized light is inconvenient because the metasurface must be precisely aligned in the polarization direction. Because of this alignment issue, circularly polarized light is commonly adopted for designing PB-phase metasurface. The transmission matrix of the linear polarization basis can be converted to that of the circular polarization basis using conversion matrix $\hat{\boldsymbol{A}}$ [Eqs. (6, 7)].

$\hat{{\boldsymbol{R}}}\left(\theta \right)=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right)& {\mathrm{cos}}\left(\theta \right)\end{array}\right] \;.$

$\hat{{\boldsymbol{A}}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ {\mathrm{j}}& -{\mathrm{j}}\end{array}\right] \;,$

$\left[\begin{array}{c}{E}_{{\mathrm{tR}}}\\ {E}_{{\mathrm{tL}}}\end{array}\right]={\mathrm{j}}{{\boldsymbol{T}}}_{xy}\left[\begin{array}{cc}0& {{\mathrm{e}}}^{-{\mathrm{j}}2\theta }\\ {{\mathrm{e}}}^{{\mathrm{j}}2\theta }& 0\end{array}\right]\left[\begin{array}{c}{E}_{{\mathrm{iR}}}\\ {E}_{{\mathrm{iL}}}\end{array}\right]\;.$

The geometric phase^38,39, also known as the Pancharatnam-Berry (PB) phase, controls the phase by changing the in-plane orientation angle of anisotropic meta-atoms.

According to , rotating the meta-atom by $\theta$ results in the phase changing by 2 $\theta$ (−2 $\theta$ ). Thus, by rotating the meta-atom from 0 to ${\mathrm{\pi}}$ , we can cover the entire phase shift from 0 to 2 ${\mathrm{\pi}}$ . The principle of geometric phase can be applied to all pairs of orthogonal polarizations, including circular, linear. Notably, the circular polarization is favored because it is less sensitive to the direction of metasurface.

${{\boldsymbol{T}}}^{{\mathrm{ circ}}}\left(\theta \right)={\mathrm{j}}{{\boldsymbol{T}}}_{xy}\left[\begin{array}{cc}0& {{\mathrm{e}}}^{-{\mathrm{j}}2\theta }\\ {{\mathrm{e}}}^{{\mathrm{j}}2\theta }& 0\end{array}\right] \;,$

where, the subscripts R and L in indicate right and left circularly polarized light, respectively. When the Jones matrix satisfies the conditions, ${{\boldsymbol{T}}}_{xx}= -{{\boldsymbol{T}}}_{yy}$ , and ${{\boldsymbol{T}}}_{xy}={{\boldsymbol{T}}}_{yx}$ , we can get a new transmission matrix, along with the transmitted electrical fields for each direction of circular polarization [Eqs. (8, 9)].

Optimization of unit cell period

The periodicity of the meta-atom is one of a key design factor. If the periodicity is too large or small, unwanted coupling between meta-atoms may occur, owing to the emergence of additional propagation modes and the occurrence of higher-order diffraction orders [Eq. (10)], thereby reducing efficiency.

where, $P$ , $\theta$ , $m$ , and $\lambda$ represent the period of the diffraction grating, angle of the diffracted light, diffraction order, and wavelength of light within the medium, respectively. As light pass through a certain medium, the wavelength within the medium can be expressed as the wavelength in air, ${\lambda }_{{\mathrm{air}}}$ , divided by the refractive index ${n}_{0}$ of the medium. Therefore, when light passes through incidentally perpendicularly on the grating surface, if $P < {\lambda }_{{\mathrm{air}}}/{{n}}_{0}$ , then the output light does not undergo diffraction and nearly passes through the medium perpendicularly. But if $P > {\lambda }_{\mathrm{a}\mathrm{i}\mathrm{r}}/{{n}}_{0}$ , diffraction can occur. As $P$ increases, higher diffraction orders gradually emerge. To determine the size of the meta-atom, it is necessary to consider not only high-order diffraction, but also the pixel size determined by the Nyquist sampling theorem, referred to here as ${P}_{{\mathrm{N}}}$ . ${P}_{{\mathrm{N}}}$ indicates how closely pixels must be positioned to avoid the loss of high-frequency components. According to this criterion, twice the pixel size must be smaller than the desired resolution⁴⁹.

${U} < \frac{\lambda }{2NA}\;.$

Additionally, the should be satisfied for designing lens with diffraction-limited resolution. Where ${U}$ , $\lambda$ and $NA$ are period of meta-atom, wavelength, and numerical aperture. The physical intuition behind is that the metasurface refracts light more steeply as the radius increases, with the refraction angle reaching its maximum at the boundary. According to the generalized Snell’s law, the upper bound of the period of a meta-atom is determined by the maximum refraction angle associated with the $NA$ , which should be achieved for diffraction-limited performance [Eq. (11)]². The period of meta-atom must be sufficiently small to accurately reconstruct the details determined by the system resolution [Eq. (11)]. A meta-atom with a period larger than this upper bound can degrade the optical resolution. This design mechanism can be generally applied into both of propagation phase and geometric phase.

$P\mathrm{sin}\left({θ}\right)={m}{λ} \;,$

Dispersion modulation

The sophisticated engineering of group delay (GD) and group delay dispersion (GDD) is being revisited as an effective solution for controlling the dispersion^40,57. GD indicates the time discrepancy for the wave packets of a polychromatic pulse to reach the focal point, whereas GDD indicates the degree of dispersion of the polychromatic pulse caused by the dispersion properties of the medium. The GDD is an essential factor for maintaining waveform consistency, accounting for variations in propagation speed owing to dispersion. Different delays occur for different wavelengths, which can lead to distortions or color dispersion⁵⁷⁻⁶¹. Achromatic design has been one of the most extensively studied fields, hence we present it as an example of dispersion modulation. As previously mentioned, controlling the GD and GDD in the metasurface is important for mitigating the chromatic dispersion. They can be optimized by adjusting the geometric features of the meta-atoms. The general phase profile of the metasurface is as follows:

where ${\omega }_{{\mathrm{d}}}$ , $\varphi (r,{\omega }_{{\mathrm{d}}})$ are the design angular frequency, the required relative phase, respectively. In Eq. (13), the first and second terms represent the constant phase delay and the linear dependency of the phase delay with respect to the wavelength, respectively. The first term can be controlled by choosing an appropriate phase modulation method, whereas the second term can be manipulated by selecting a suitable meta-atom⁵⁰. Chen et al.¹² used coupled meta-atoms consisting of two closely placed nanofins to enhance design flexibility, enabling nearly zero GDD across a wide range of wavelengths. Without the design capability of the GD and GDD, high-quality imaging is restricted owing to chromatic aberrations^12,61−64. Therefore, rigorous achromatic design strategies should be considered for high-quality bioimaging.

${\varphi }\left({r},{\omega }\right)= -\frac{\omega }{c}\left(\sqrt{{r}^{2}+{f}^{2}}-f\right),$

The dispersion is the deviation of light from the original path in a wavelength-dependent manner as it passes through a dispersive medium. The dispersion modulation is a common issue in the field of metasurfaces for wavelength dependent designing, such as achromatic metasurfaces^12,50−52 and spectrometer⁵³⁻⁵⁶. It is important to strictly control the dispersion as it can cause either positive (e.g., spectrometer) or negative effect (e.g., chromatic aberration) depending on its applications.

where $c$ , $\omega$ , f and $r$ are the speed of light, angular frequency, focal length, and radial coordinate. Understanding the wavelength dependency of metasurfaces becomes easier with the Taylor expansion of the phase profile¹². The $\varphi (r,\omega )$ can be expanded into a Taylor series around the design frequency, which corresponds the center wavelength:

$\begin{split} {\varphi }\left({r},{\omega }\right)=&\varphi \left(r,{\omega }_{{\mathrm{d}}}\right)+{\left.\frac{\partial \varphi \left(r,\omega \right)}{\partial \omega }\right|}_{\omega ={\omega}_{{\rm{d}}}}\left(\omega -{\omega }_{{\mathrm{d}}}\right)\\ &+{\left.\frac{{\partial }^{2}\phi \left(r,\omega \right)}{2\partial {\omega }^{2}}\right|}_{\omega ={\omega}_{\rm{d}}}{(\omega -{\omega }_{{\rm{d}}})}^{2}+\dots , \end{split}$

Materials for metasurface

Proper selection of materials properly is critical for biological imaging in terms of imaging quality, fabrication and biocompatibility. The optical properties of materials, such as refractive index and optical extinction coefficient, greatly influence the phase design strategy and degree of freedom, as they govern the phase delay, transmission and polarization of matesurfaces in a wavelength dependent manner. The material should be compatible with nanofabrication for building meta-atoms. For biological applications, another crucial condition is biocompatibility. Metasurfaces that do not directly contact object being imaged are relatively free from biocompatibility concerns. However, in applications where direct contact occurs such as hyperlenses and local surface plasmonic resonance (LSPR), material selection should be carefully considered. It is worth noting that biocompatibility of designed metasurfaces should be tested before in vivo and in vitro applications since the biocompatibility depends not only on the materials, but also on the structure, size and species of subject. For example, although gold is widely known for its biocompatibility and used in plasmonic applications, gold nanoparticles can exhibit cytotoxic effect at certain sizes and concentrations⁶⁵. In this section, we classified widely used materials for metasurfaces into two broad categories: plasmonic, dielectric materials and tunable materials.

Plasmonic material

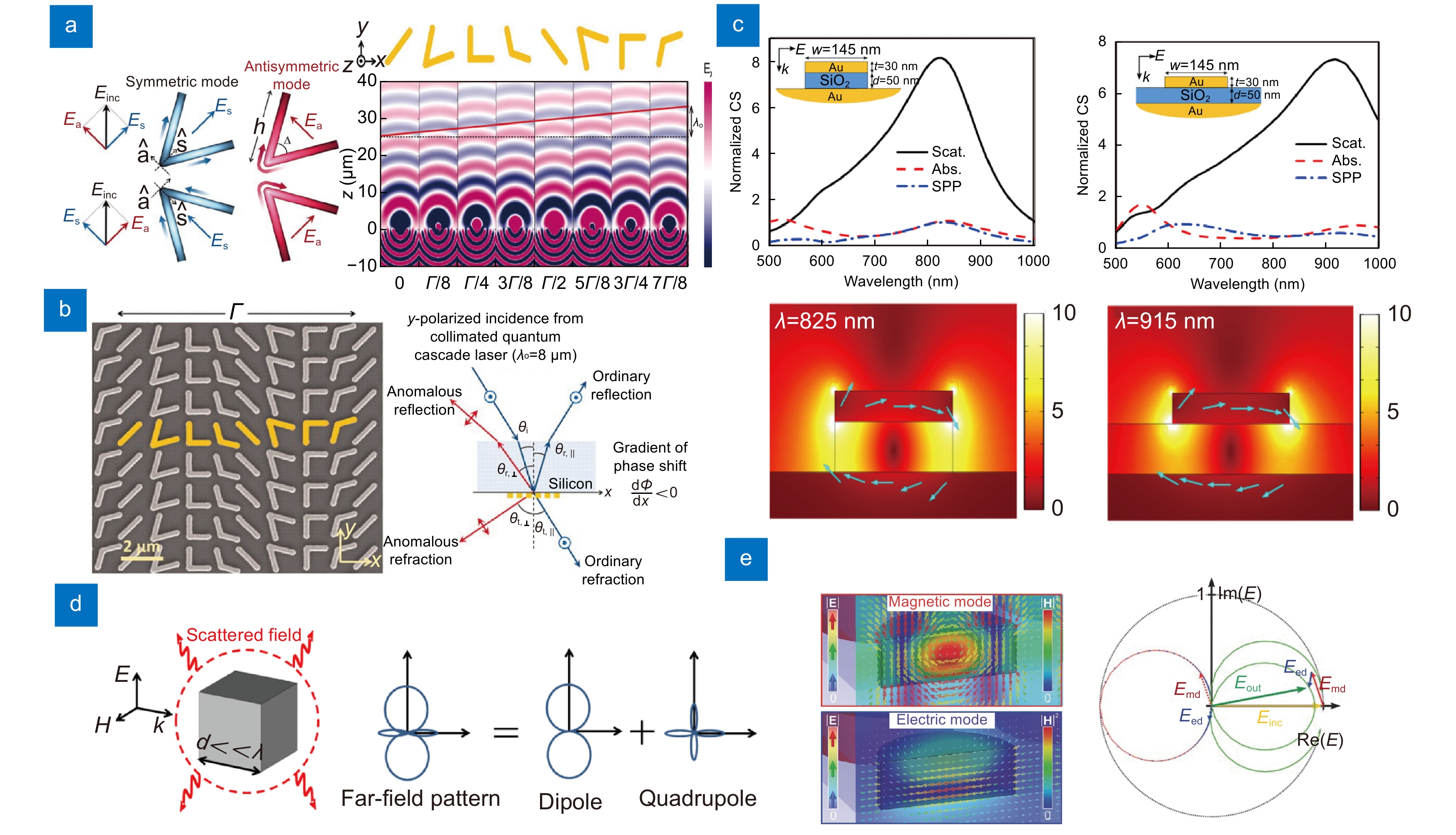
Plasmonic resonators can control the phase, amplitude, polarization, and dispersion of light by adjusting the material properties, geometry, and vibrational frequency. Surface plasmonic resonators (SPR) have been adopted as unit cells for metasurfaces owing to their versatility. However, SPR has limitations arising from a phenomenon known as momentum mismatch^68,69, which leads to efficiency losses⁷⁰. This mismatch is a critical factor that constrains the performance of metasurfaces, particularly in terms of energy transfer and light manipulation at the nanoscale⁷¹. To address these challenges, LSPR is predominantly utilized in metasurfaces⁴⁷. SPR primarily occurs in continuous metallic films, whereas LSPR occurs in localized nanostructures, such as nanoparticles and nanorods, generating strong electromagnetic fields within the localized regions. This makes it suitable as a building block for metasurfaces capable of modulating light properties⁷². As depicted in , the four V-shaped plasmonic metal antennas with different length and angles can modulate the phase delay of incident light with a phase interval of ${\rm{\pi}}$ /4. These V-antennas exploit symmetric and anti-symmetric modes, which are simultaneously excited by adjusting the polarization angle of the incident light to be within the parallel and perpendicular directions⁷³. To find optimized structures that cover the 0 to 2 ${\mathrm{\pi}}$ phase while achieving large amplitudes, the optical response of these meta-atoms was analytically calculated by varying the length of the two equal arms and the angle between them. Four antennas with high amplitudes were chosen that cover the 0 to ${\mathrm{\pi}}$ range with a ${\mathrm{\pi}}$ /4 step size, and their mirror-symmetric structures were simply used to cover the remaining ${\mathrm{\pi}}$ to 2 ${\mathrm{\pi}}$ phase range. By integrating these modal properties with the flexibility to select the geometric configuration of the antenna, an array can be designed to achieve a 2 ${\mathrm{\pi}}$ phase range with consistent scattering amplitudes^{29,66,74−78}.

Another promising plasmonic resonator is the gap surface plasmonic resonator (GSPR)^79,80. While LSPR is generated in single metallic nanostructures, GSPR is distinctly characterized by its occurrence in narrow gaps between two metallic nanostructures. As shown in Fig. 3(c), the metal surfaces separated by a thin dielectric spacer dramatically enhanced the electromagnetic field in the localized region. This feature allows GSPR to enable more potent electromagnetic field amplification and efficacious control over the phase, amplitude, and polarization of the reflected light compared to LSPR^81,82. Furthermore, high reflection efficiency of GSPR (>80%), making it suitable for various bioimaging applications⁸²⁻⁸⁵.

Surface plasmons (SPs)⁶⁶ are surface electromagnetic waves that propagate at the metal-dielectric interface and decay exponentially in directions perpendicular to the interface. A plasmonic resonator involves the oscillations of the electron charge density at the metal surface, which are enhanced when the metal is adjacent to a dielectric medium. These combined phenomena facilitate the manipulation of electromagnetic waves at the subwavelength scale, offering advanced control in nanoscale electromagnetic applications⁶⁷.

$Figure 3. Representative metasurfaces consist of plasmonic and dielectric materials. (a) V-shaped plasmonic meta-atom. The V-antennas activate symmetric and antisymmetric modes depending on the incident light. The unit cells are periodically arranged to manipulate reflection and refraction of light. (b) SEM image of V-antennas showing the periodic arrangement of unit cells (left). A schematic illustrating the phase-delayed according to the generalized Snell's law (right). (c) Scattering, absorption, and SPP cross-sections of gap surface plasmon resonator (top). Distribution of electric field enhancement (bottom). (d) A dielectric scatterer with a typical size considerably smaller than the operating wavelength. Dielectric materials are chosen for their low-loss and high refractive index properties, which allow efficient phase and amplitude control. (e) Electric and magnetic field distribution of the silicon nanodisk metasurface (left). overlapped vector diagram of the electric field (right). Electric and magnetic dipole resonances can be simultaneously generated and overlapped to suppress the reflection of the metasurface. Through the careful design of the dielectric structure, it is possible to control the transmittance using resonance control. Figure reproduced with permission from: (a, b) ref.29, American Association for the Advancement of Science; (c) ref.82, Optics express; (d) ref.88, Optics express; (e) ref.89, John Wiley and Sons.$

Figure 3. Full-Size Img PowerPoint

Representative metasurfaces consist of plasmonic and dielectric materials. (a) V-shaped plasmonic meta-atom. The V-antennas activate symmetric and antisymmetric modes depending on the incident light. The unit cells are periodically arranged to manipulate reflection and refraction of light. (b) SEM image of V-antennas showing the periodic arrangement of unit cells (left). A schematic illustrating the phase-delayed according to the generalized Snell's law (right). (c) Scattering, absorption, and SPP cross-sections of gap surface plasmon resonator (top). Distribution of electric field enhancement (bottom). (d) A dielectric scatterer with a typical size considerably smaller than the operating wavelength. Dielectric materials are chosen for their low-loss and high refractive index properties, which allow efficient phase and amplitude control. (e) Electric and magnetic field distribution of the silicon nanodisk metasurface (left). overlapped vector diagram of the electric field (right). Electric and magnetic dipole resonances can be simultaneously generated and overlapped to suppress the reflection of the metasurface. Through the careful design of the dielectric structure, it is possible to control the transmittance using resonance control. Figure reproduced with permission from: (a, b) ref.²⁹, American Association for the Advancement of Science; (c) ref.⁸², Optics express; (d) ref.⁸⁸, Optics express; (e) ref.⁸⁹, John Wiley and Sons.

Although GSPR achieves high reflection efficiency, reducing optical loss remains a challenge in the design of highly efficient metasurfaces. This loss is particularly critical for visible light and communication wavelengths. Commonly used plasmonic materials such as gold and silver have limitations in the visible range owing to the inherent loss of metals and heat dissipation^86,87. Materials science and design methods for plasmonic resonators have been actively investigated to address these issues.

Dielectric material

${d}=\frac{\lambda }{{\mathrm{\Delta }n}_{{\mathrm{eff}}}}\;.$

where, ${k}_{0}$ represents the wavenumber, defined as $2{\mathrm{\pi}} /\lambda$ , where $d$ is the thickness of the meta-atom, $\lambda$ is the wavelength, and ${\mathrm{\Delta }n}_{{\mathrm{eff}}}$ is the difference in refractive index experienced by light as it passes through two different media¹⁰³. The ${\mathrm{\Delta}} {n}_{{\mathrm{eff}}}$ is determined by the volume weighted sum of refractive indices of both the surrounding medium (typically air) and the materials of the meta-atoms. For example, if the size of a structure increases, causing its volume to expand, the effective index $\mathrm{\Delta }{n}_{{\mathrm{eff}}}$ also increases, leading to significant phase delay¹⁰⁴.

Dielectric meta-atoms with high refractive indices can effectively couple with various multipolar modes of Mie resonances⁹¹, allowing for efficient control over the phase changes, polarization, and amplitude⁹²⁻⁹⁵ []. Mie resonances occur when dielectric meta-atoms have a distinct refractive index in contrast with the surrounding medium. This resonance affects the electric and magnetic dipole moments by interacting with incident light⁸⁸. Dielectric meta-atoms can cover a phase range from 0 to 2 $\mathrm{\pi }$ by finely controlling the resonance spectrum of electric and magnetic dipoles based on the material and shape of the meta-atoms. As shown in Fig. 3(e), the scattering properties can be controlled by designing meta-atoms that overlap the electric and magnetic dipole resonances⁸⁹, as explained by the Kerker effect⁹⁶. According to the Kerker effect, by carefully designing the dielectric structure, one can control the electric and magnetic resonances to regulate the transmittance and eliminate backscattering^97,98. In dielectric meta-atoms, interference manifests in the forward direction when the amplitudes of the electric and magnetic multipoles are in phase; conversely, backward interference arises when they are out of phase^89,98−100. Unlike metal resonators, dielectric resonators do not require magnetic materials for optical-scattering control¹⁰¹. However, such resonances generally occur in narrow bandwidths, leading to low transmittance and difficulty in phase modulation over a wide range.

The fill factor (FF), signifying the ratio of space filled by specific elements within a structure, allows for the manipulation of the phase shift ${\mathrm{\Delta }}\phi$ , where FF denotes the area ratio occupied by the meta-atoms. To cover a phase shift ${\mathrm{\Delta }}\phi$ of $2{\mathrm{\pi}}$ , the thickness of the meta-atom must follow Eq. (15)⁴⁰. Precise control over the propagation phase can be achieved by tuning the effective refractive index and thickness of the meta-atom, facilitating the design of the phase in planar optical elements¹⁰⁵. Recently, there has been an increase in attempts of using inverse design methods^{98,99,101,106} for overcome the limitation of narrow bandwidth. And also there are some try of optimizing waveguides to adjust the dispersion, thereby creating metasurfaces for broadband wavelength⁵¹.

Owing to their low efficiency and high intrinsic ohmic loss⁹⁰, metal resonators are unsuitable for use in resonant metamaterials operating at frequencies above the infrared range. Efforts to address this issue have led to increased research on the utilization of low-loss dielectric materials in metasurfaces. The ability to regulate magnetic and electrical resonances by manipulating the geometry and spacing of the dielectric resonators is an appealing aspect of metasurface research^87,88. Dielectric materials operate based on the confinement of electromagnetic fields and require a high refractive index. Typically, dielectric meta-atoms have lower losses than metals; however, they also have lower refractive indices, necessitating the selection of appropriate materials based on the operating wavelength to design meta-atoms. Dielectric metasurfaces can function as either resonators or waveguides. In this section, we will discuss these two forms separately to provide a clear understanding of their distinct mechanisms and applications.

${\mathrm{\Delta }}\phi ={\mathrm{\Delta }n}_{{\mathrm{eff}}}{k}_{0}d\;,$

Dielectric materials with high refractive indices can effectively refract and confine light, functioning as waveguide modes that facilitate enhanced light-matter interactions. Operating as waveguide elements allows them to work over a broad bandwidth, demonstrating high transmittance and complete phase modulation. The energy of the incident light wave, which is limited inside the meta-atom, delays the propagation phase of the light, enabling phase accumulation^32,102. The magnitude of phase shift ${\rm{\Delta }}\phi$ is related to the optical path difference, which depends on the effective refractive index and thickness [Eqs. (14, 15)].

Tunable material

One popular class is phase change materials (PCMs), which undergo transitions between states (e.g., amorphous and crystalline) depending on the external conditions, resulting in the significant change of optical properties. Chalcogenide compounds such as Ge₂Sb₂Te₅ (GST)¹⁰⁷, Ge₂Sb₂Se₄Te (GSST)¹⁰⁸ are representative examples of PCMs, which can reversibly switch their crystalline state depending on temperature, resulting in refractive change. These materials can be easily and quickly modified using high energy pulse laser or electrothermal devices, making them widely used for creating reconfigurable metasurfaces^107−109. Vanadium dioxide (VO₂)^110−112 is another promising PMC due to its metal-insulator transition (MIT) characteristics reasonably low temperature (~68 ˚C), making it easy to switch¹¹³ VO₂ is generally employed for creating metasurfaces working in the infrared band as it is transparent and tunable within these ranges^113−116. PCMs, which can switch states through various external stimuli, offer the potential to control optical responses in multiple ways.

Light modulation is sometimes required during optical imaging in various purposes, such as switching between different imaging modes. Generally, spatial light modulator (SLM) has been employed for these purposes, but it is associated with drawbacks including high cost, complicated system requiring maintenance, and limited diffraction angles due to the large pixel sizes. As an alternative or complement, tunable matasurfaces are being explored for specific applications. Selecting appropriate materials with optical properties that can be modulated by external stimuli, such as electric fields or temperature, is crucial for implementing these devices. In this section, we will briefly discuss representative materials widely used for creating tunable metasurfaces.

Liquid crystal (LC)^117,118 is also often used to make tunable metasurfaces. It has anisotropic optical properties (e.g., anisotropic dielectric constant) and respond to external electric fields, originating from its high aspect ratio molecular structure¹¹⁹. When external electric field is applied to a LC molecule, they align in the direction of electric field, thereby modifying their effective refractive index, which modulates the phase of certain polarization direction of incident light^120,121. Additionally, LC cells provide real-time responsiveness and high transparency, enabling fast and efficient modulation. Combining LC cells with metasurfaces provides opportunities for various applications such as mode switching¹²² r varifocal metasurfaces¹²³. Mechanical stress can also adjust phase of metasurfaces if flexible substrates is employed. By applying mechanical stress to metasurfaces fabricated on flexible substrates, the geometric parameters of meta-atoms are altered, finely tuning the optical response¹²⁴ since phase profile of metasurface is highly sensitive to the structures of meta-atoms¹²⁵. This approach offers the advantages of simple structural design and low cost, as it does not require additional devices for stimulation¹²⁶. While the range of working wavelengths is limited by the material properties, the development of advanced materials provides opportunities for more flexible and versatile design. In conclusion, by leveraging the properties of various materials, it is possible to implement tunable metasurfaces with more flexible and verstile designs. Such designs are essential for the multipurpose commercialization of metasurfaces.

Applications

To acquire high-quality images from biological samples, several parameters of optical system should be optimized, such as NA, field of view (FOV), depth of field (DOF), achromaticity, and imaging time. These parameters should be carefully tuned depending on the imaging modalities to build a high-performance optical system since they trade off against each other and typically cannot be optimized simultaneously. For example, while utilizing high NA metasurfaces enables high-resolution imaging, it reduces the FOV and DOF, restricting the large-field 3D bioimaging. Thus, many kinds of optimization techniques have been adopted to find optimal metasurfaces for bioimaging¹²⁷. Due to fabrication difficulties, the available size of metasurfaces is limited to around ~2 mm, which also restrict the imaging FOV. The short DOF or small FOV can be somewhat compensated by using 3D scanning system (e.g., galvo or motorized stage), but this comes at the expense of imaging time and signal-to-noise ratio (SNR).

The point spread function (PSF) engineering could be a good solution for optimizing the system for microscopic imaging. It is particularly worth noting the utilization of non-diffracting light, which preserves the size and intensity profile during propagation, in the field of bioimaging^128,129. Metasurfaces are well-optimized for this kind of beam shaping since they are specialized for modulating polarization, diffraction, and amplitude of light, which is not possible with classical optics^20,130−134. The Bessel beam, the most popular non-diffracting beam, is almost a basic option for building large DOF imaging system without degradation of lateral resolution. It has also been employed for enlarging the FOV in perpendicular illumination systems such as light sheet microscopes¹³⁵. Variations of the Bessel beam is still actively being studied to form sharper and longer PSFs. The vortex beam, which is another subset of non-diffracting beam, is an essential component for edge-detection microscopy^122,136,137. In this section, we introduce various advanced imaging techniques using metasurfaces. We will discuss how the metasurfaces are incorporated into imaging systems to overcome the limitations of conventional optics, referring to specific application examples.

Metasurfaces for cell imaging applications

Owing to its simplicity, cells have been used as a basic object for imaging in the field of biology. They are often used in a wide range of biological studies such as clinics, diagnostics, and drug screening. Due to their importance, a lot of imaging techniques adapted for cell imaging have been developed. In this section, various metasurfaces for advanced cell imaging techniques are discussed.

Super-resolution imaging

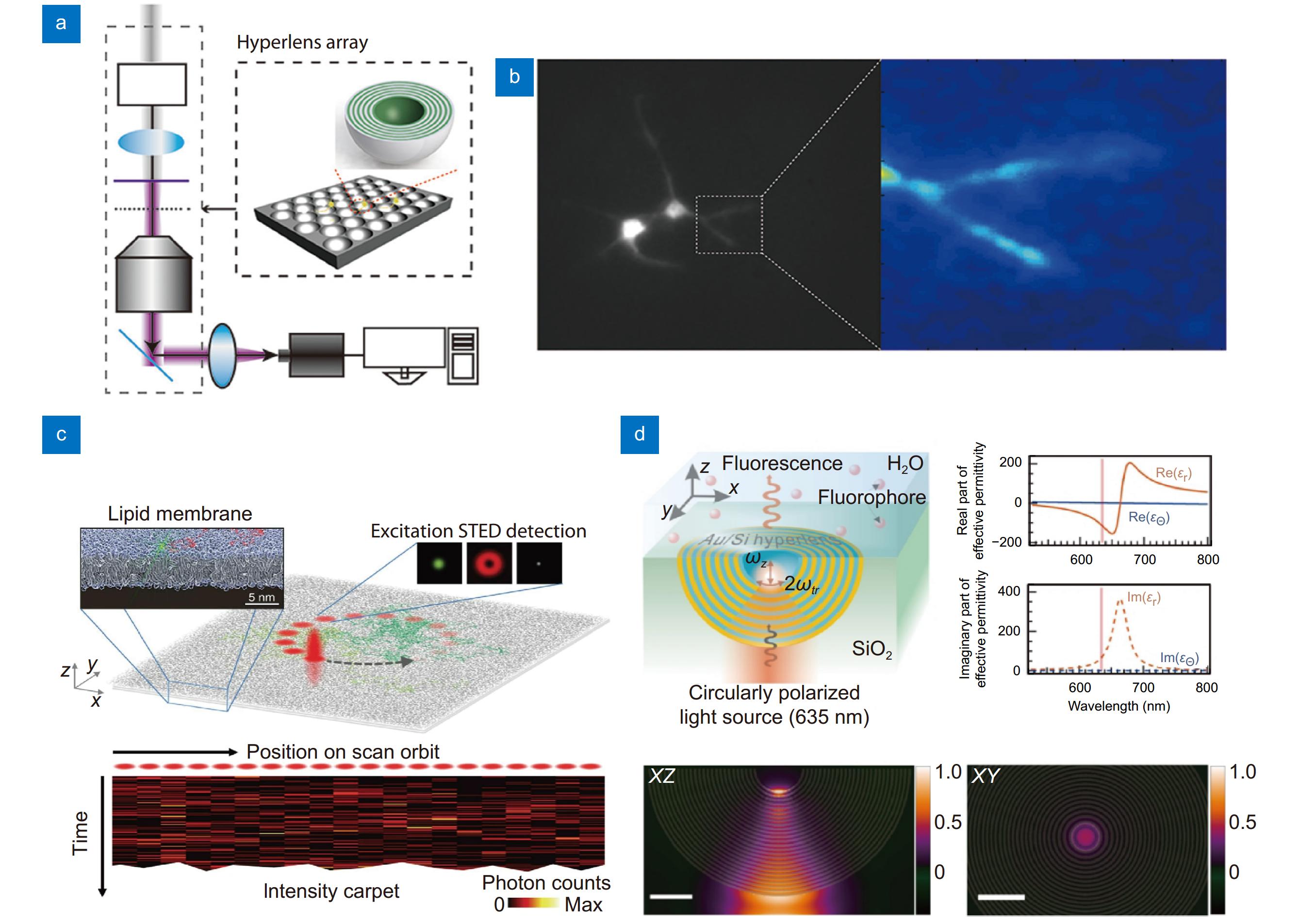
Figure 4. Metasurfaces for super-resolution techniques for cell imaging application. (a, b) Optical setup of hyperlens-based (a) super-resolution imaging system, and (b) fluorescent image of cultured neuron. (c, d) Super-resolution FCS setup based on (c) STED, and (d) hyperlens. Scale bar: 200 nm. Figure reproduced with permission from: (a, b) ref.15, American Chemical Society; (c) ref.151, Springer Nature; (d) ref.152, Optical Society of America.

Figure 4. Full-Size Img PowerPoint

Metasurfaces for super-resolution techniques for cell imaging application. (a, b) Optical setup of hyperlens-based (a) super-resolution imaging system, and (b) fluorescent image of cultured neuron. (c, d) Super-resolution FCS setup based on (c) STED, and (d) hyperlens. Scale bar: 200 nm. Figure reproduced with permission from: (a, b) ref.¹⁵, American Chemical Society; (c) ref.¹⁵¹, Springer Nature; (d) ref.¹⁵², Optical Society of America.

$\frac{{\omega }^{2}}{{c}^{2}}=\frac{{k}_{\parallel }^{2}}{{ \epsilon}_{\parallel }}+\frac{{k}_{\perp }^{2}}{{ \epsilon }_{\perp }}\;.$

The initial versions of hyperlenses¹⁴⁸ were also slab lenses¹⁴⁵, like superlenses. However, cylindrical, and spherical shapes were found to be considerably more practical than slab shapes. These shapes are more suitable for performance optimization, including ensuring equivalent path lengths and minimizing surface scattering^14,146,149. The first biological imaging using a spherical hyperlens array was performed by Lee et al.¹⁵ [Fig. 4(a, b)]. They captured fine neuronal structures, which are crucial for investigating the functionality of the brain and resolved features of approximately 150 nm at a wavelength of 410 nm. Another potential biological application of hyperlenses is single-molecule studies in cells based on fluorescence correlation spectroscopy. The focal volume, the size of the PSF, in single molecular imaging is related to the available concentration of biomolecules and sensitivity for measuring diffusion heterogeneity¹⁵⁰. A previous study revealed the spatiotemporal heterogeneity and hindered diffusion of lipid interactions using scanning STED-FCS (sSTED-FCS), which is not available with diffraction-limited focal volumes [Fig. 4(c)]¹⁵¹. In 2023, Barulin first proposed the theoretical feasibility of hyperlenses for sub-diffraction single-molecule imaging in cell membrane structure through a simulation study [Fig. 4(d)]¹⁵². They simulated the nanoscale dynamics of lipids in the cell membrane and demonstrated the possibility of capturing location-dependent hindered diffusion with a spatial resolution of 40 nm using a metal-dielectric hyperlens.

The optical resolution is defined as the minimum distinguishable distance between two points and is determined by the NA and wavelength of the optical systems. Even when enhanced using high-NA optics or short wavelengths, the resolution does not improve beyond a certain level (~250 nm) at visible wavelengths owing to the physical limit of diffraction, known as the ‘diffraction limit’^138,139. In biological imaging, the diffraction limit restricts the quantitative imaging of subcellular networks, such as mitochondria, microtubule networks, and synaptic connections, which are related to cellular functionalities. Furthermore, molecular studies suffer from limited optical resolution, for example, in investigating the spatial distribution of membrane protein and molecular interactions. Various super-resolution imaging techniques have been adopted in the field of biological imaging based on PSF engineering (i.e., STED), structured illumination (SIM), and single molecule localization (i.e., PALM, STORM) to overcome the diffraction limit^140,141. However, these techniques require a complex and cost-inefficient optical setup and computationally intensive postprocessing. Moreover, some techniques are available only with special fluorescent labeling and are not used for general imaging.

To achieve diffraction-unlimited resolution, the behavior of wave propagation should be considered. According to angular spectrum theory, waves are categorized into propagating and non-propagating waves, termed evanescent waves. Evanescent waves are exponentially decaying waves near a light source that convey structural information smaller than its wavelength^142,143. As they carry high-frequency structural information, capturing evanescent waves is essential for achieving super-resolution. In 2000, John Pendry proposed the concept of a perfect lens capable of producing super-resolution images using negative-index materials¹⁴⁴. However, the implementation of negative-index material is challenging because it does not exist in nature. Fortunately, Pendry proved that a material can work as a perfect lens if it satisfies either negative permittivity or negative permeability in polarized light. Although Pendry showed that lossy metals, such as silver, can act as perfect lenses, they cannot recover images exactly same as the real object, even in theory, owing to the damping loss of the metal. An imperfect lens is defined as a superlens. The first superlens operating in the optical regime was demonstrated using metamaterials in 2005 by Fang et al.¹⁴⁵, which is a promising technique for satisfying the necessary conditions for superlenses, given its versatility in modifying optical properties. However, conventional imaging remains impractical because it operates in the near-field regime. A more practical approach is to employ a hyperlens consisting of hyperbolic metamaterials with a highly anisotropic permittivity¹⁴⁶. Although the hyperlens consist of hyperbolic “metamaterial” and is termed “lens”, its working principle is entirely different to the metalens, which is specialized for focusing light and imaging. Thus, there is controversy regarding the categorization of hyperlens as a metalens². However, as we comprehensively cover the bioimaging techniques primarily based on metasurface with a few instances involving metamaterial, we introduce hyperlens in this section. A common way to implement hyperlens is to create a periodic structure by alternating two different materials with subwavelength thicknesses. The wave propagating in the direction of the anisotropic axis undergoes a different effective permittivity and dispersion relationship []¹⁴⁷, where $\mathrm{\omega }$ , $c$ , $k$ , $\epsilon$ represent the angular frequency, speed of light in vacuum, wavevector, relative permittivity, respectively. The subscripts $\parallel$ , $\perp$ indicate components parallel and perpendicular to the propagation direction of wave, respectively. The ${\epsilon }_{\parallel }$ , and ${\epsilon }_{\perp }$ should have the opposite sign.

Typically, the metasurfaces for super-resolution imaging based on near field approaches suffer from optical loss and sample mounting¹⁵⁹. To achieve super-resolution imaging using them, the metasurfaces should be placed or fabricated near the samples. Furthermore, a strong light source is needed to obtain a strong enough signal from the sample due to the optical loss of near field metasurfaces, which cause phototoxicity of biological samples. To overcome these limitations, super-oscillatory lens (SOL) has been suggested for achieving super-resolution imaging through the far field approaches¹⁶⁰. The phenomenon of super-oscillation refers to the local oscillation in band-limited function that oscillate faster than their fastest Fourier components. This phenomenon was originally discussed by Aharonov¹⁶¹, and its application for optical super-resolution was suggested by Michael Berry and Sandu Popescu¹⁶⁰. Berry et al. predicted that super-oscillation can be generated by a diffraction grating and delivered through the propagating beam without evanescent wave. The first experimental observation of the super-oscillation generated from quasicrystal array of nanoholes in a metal screen, resulting in a ~220 nm of hot spot (~0.37λ) opened the possibility of far field super resolution imaging¹⁶².

Metasurfaces also can be used for SIM, which achieves super-resolution by combining images illuminated by several patterns. The maximally achievable spatial frequency of conventional SIM is determined by the sum of the illumination and detection spatial frequencies¹⁶. Generally, only ~2 times resolution enhancement can be attained with conventional SIM compared to diffraction limited resolution, since the spatial frequencies of illumination and detection are restricted by the diffraction limit. Extending detection spatial frequency is more difficult than increasing the illumination frequency in optical regime. Thus, many efforts have been focused on increasing the illumination frequency, particularly using near field. Plasmonic materials are specialized for generating high-resolution near field^17,153−157. Notably, hyperbolic materials can be one of the easiest available solutions, attributed to their simple fabrication method. Lee et al.¹⁵⁸ developed speckle metamaterial-assisted illumination nanoscopy (speckle-MAIN) and reconstructed high-resolution images using blind-SIM algorithm, accomplishing a resolution of ~40 nm. They fabricated hyperbolic metasurfaces consisting of periodically stacked Ag and SiO₂ layers with a root mean square roughness of ~1.1 nm, generating high-resolution and near field speckle under illumination. Then, they illuminated excitation light through the vibrating multimode fiber to obtain enough random speckle patterns. This hyperbolic metasurface assisted SIM method also successfully works for label-free imaging, as well. Lee et al. also substantiated the feasibility of hyperbolic material assisted illumination for label-free imaging. They developed hyperbolic material enhanced scattering (HMES) nanoscopy with dark-field detection system, which improved resolution by a factor of 5.5 times than diffraction limit¹⁵⁸. Since it is challenging to directly detect near field with optical detection in visible range, SIM is a remarkable method for recovering high-resolution near field speckles, unlike to the superlens.

By sophisticated design, practical SOL metasurfaces have been fabricated by patterning a periodically aligned concentric nanostructure^159,163,164. Qin et al. experimentally resolved structures as small as 65 nm (~0.16λ) using their long working distance (~135λ) supercritical lens (SCL)¹⁶⁵ . They adopted scanning microscope with a high-speed piezo stage to obtain large-area and high-quality images, achieving imaging speeds 16 times faster than previous study¹⁵⁹. Overcoming limitations such as chromatic aberration^166,167, extending DOF^168−172, short working distance and limited FOV is indispensable for more practical bioimaging. Theoretically, functions for super-oscillation can make sharp peaks as small as desired at the expense of several parameters such as intensity of side lobe, bandwidth, and peak intensity¹⁶⁴. Thus, it is important to maintain the balance between these parameters for practical imaging applications. In a recent study, Li et al. simultaneously optimized these parameters of SOL by applying a multi-objective genetic algorithm¹²⁷. Their apochromatic SOL exhibited awesome performance with ~0.53λ (488 nm) resolution, including >10λ of DOF, 428 µm of focal distance and suppressed side lobes. Using this advanced SOL, they first acquired 3D, multicolor fluorescent images of neuronal tissue. These consecutive and sustained reports of super-resolution metasurfaces imply the potential of metasurfaces in advanced bioimaging.

Edge-detection metasurface

In the field of bioimaging, computational image processing has become indispensable for advancing optical imaging techniques. However, these techniques often require significant computational resources and processing time, which prohibit the real-time monitoring of biological activities. A promising solution to alleviate this burden is to employ an special optical elements for all-optical analog image processing, similar to hardware acceleration in the field of electronics¹⁷³. Metasurfaces provide numerous degrees of freedom for designing image processing filters and have the potential to process extensive biological data with minimal computational resources¹⁷⁴. Edge-detection is a key filter used in image processing that highlights object outlines by recognizing abrupt intensity gradients at object boundaries^175−177. This typically involves the convolution of kernels or Fourier transformations, which consume significant computational resources¹⁷⁸. Normally, this process can be achieved with phase modulation devices such as SLM by creating spiral phase filter at Fourier plane. However, this method tends to increase the overall system size^179−181. Recently, edge-detection metasurfaces have been actively studied to replace conventional bulky optical elements. Metasurface-based all-optical edge-detection enables a more compact and simpler optical system by eliminating the need for additional components. This method not only improves the design flexibility but also facilitates faster image processing, making it highly suitable for the miniaturization of microscopes and imaging devices^182,183. This technology can be utilized for the label-free imaging of transparent samples, such as cells or tissues [Fig. 5(a)].

Edge-detection can also be implemented using spiral phase metasurfaces that incorporate a hyperbolic phase with a topological charge of 1^122,188,189. The amplitude and phase distributions of the spiral metasurface at the focal plane exhibited ring and spiral shapes, respectively [Fig. 5(c)]. The uniform regions are cancelled out because of destructive interference, allowing only high-contrast areas to be observed. However, their applicability for general purpose imaging has been limited, as those methods heavily rely on 4f systems with coherent illumination. Recently, Wang et al.¹³⁷ developed a metasurface that operates with an incoherent light source by digitally subtracting images taken from different linearly polarized lights [Fig. 5(d)]. Each image is captured using polarization camera with polarization-multiplexed metasurfaces having hyperbolic (x-polarization) and spiral (y-polarization) phases. This technique delineates the contours of an object more clearly even with incoherent light, presenting an excellent approach for general purpose imaging. Also Zhou et al.¹⁹⁰ demonstrated a Laplace differentiator based on a metasurface with toroidal dipole resonance. This metasurface achieved 2D second-order edge detection, significantly enhancing image processing capabilities. Recently, Chu et al.¹⁹¹ experimentally demonstrated a meta-microscope that achieves both optical and digital phase contrast imaging. This technology leverages deep learning models to enable high-contrast and accurate imaging. Optical phase contrast imaging uses a spiral phase metasurface to enhance edge contrast, while digital phase contrast imaging converts bright-field images into edge enhanced images using deep learning algorithms. This research highlights the potential of metasurface multifunctionality using deep learning.

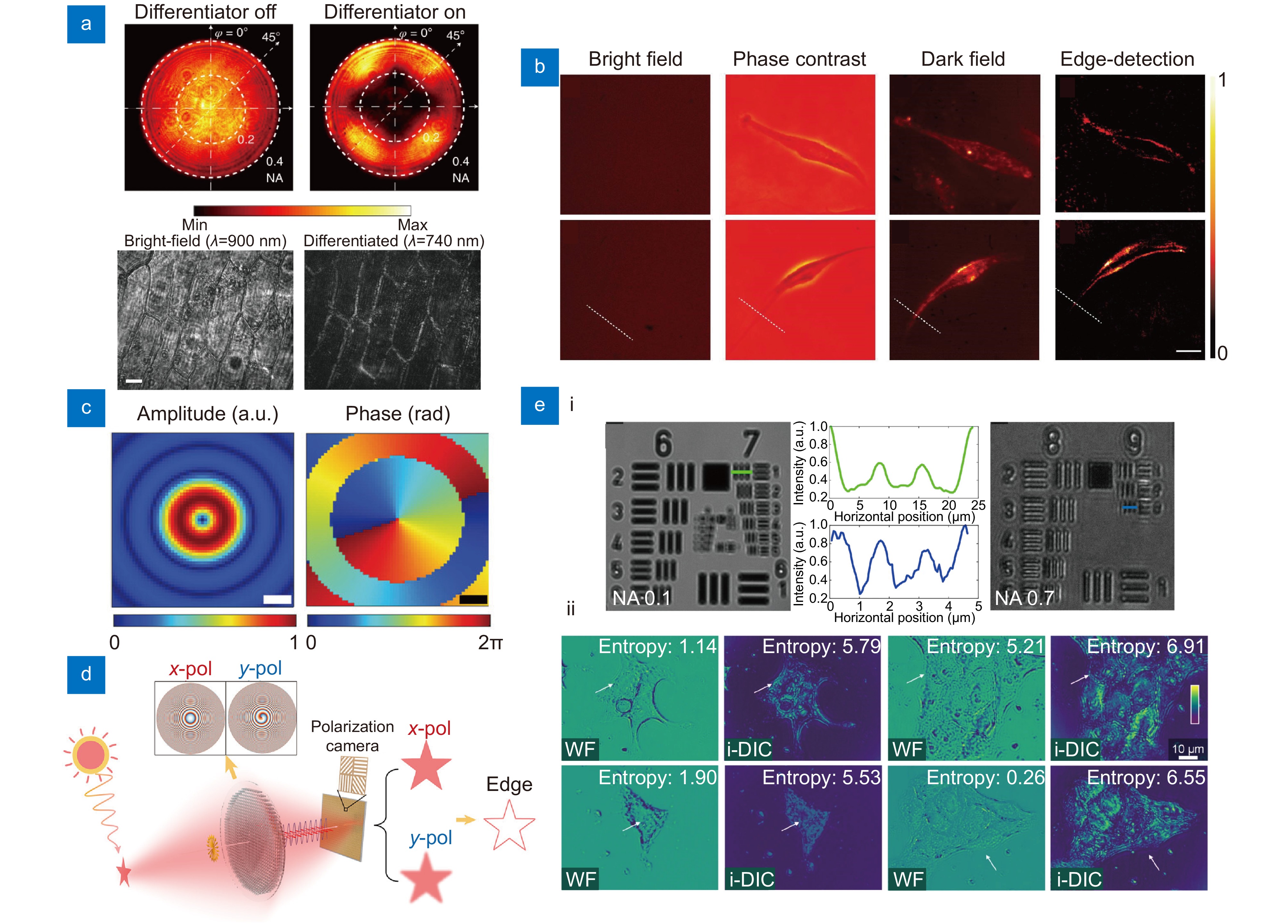
Figure 5. Edge-detection metasurfaces for cell imaging applications. (a) Images obtained at back focal plane of a standard metasurface and nanophotonic differentiator metasurface (top). Onion epidermis obtained with and without differentiator metasurface (bottom). Scale bar: 50 μm. (b) Human umbilical vein endothelial cells (top) and human bronchial epithelial cells (middle) taken by using brightfield, phase contrast, dark field, and edge-detection, respectively. Scale bar: 100 μm. (c) Amplitude and phase distributions calculated using the angular spectrum method (ASM) at the focal plane of a spiral metasurface. Scale bar: 250 nm. (d) Edge-detection metasurface compatible to incoherent light for general purpose imaging. (e) (i) Metasurface-assisted DIC image of the USAF 1951 resolution test chart under NA of 0.1 and 0.7, respectively. (ii) Images captured with wide-field and i-DIC microscope. Figure reproduced with permission from: (a) ref.182, Springer Nature; (b) ref.186, Oxford University Press; (c) ref.188, John Wiley and Sons; (d) ref.137, American Chemical Society; (e) ref.19, Springer Nature.

Figure 5. Full-Size Img PowerPoint

Edge-detection metasurfaces for cell imaging applications. (a) Images obtained at back focal plane of a standard metasurface and nanophotonic differentiator metasurface (top). Onion epidermis obtained with and without differentiator metasurface (bottom). Scale bar: 50 μm. (b) Human umbilical vein endothelial cells (top) and human bronchial epithelial cells (middle) taken by using brightfield, phase contrast, dark field, and edge-detection, respectively. Scale bar: 100 μm. (c) Amplitude and phase distributions calculated using the angular spectrum method (ASM) at the focal plane of a spiral metasurface. Scale bar: 250 nm. (d) Edge-detection metasurface compatible to incoherent light for general purpose imaging. (e) (i) Metasurface-assisted DIC image of the USAF 1951 resolution test chart under NA of 0.1 and 0.7, respectively. (ii) Images captured with wide-field and i-DIC microscope. Figure reproduced with permission from: (a) ref.¹⁸², Springer Nature; (b) ref.¹⁸⁶, Oxford University Press; (c) ref.¹⁸⁸, John Wiley and Sons; (d) ref.¹³⁷, American Chemical Society; (e) ref.¹⁹, Springer Nature.

One promising approach for edge detection is nonlocal metasurface, which manipulate light in momentum domain. The term “nonlocal” indicates that meta-atoms of the metasurface interacts with the incident light in a collective manner rather individual elements^192−194. This approach offers new opportunities for designing novel functions, such as greater degree of freedom, compressing space for light propagation, and creating mathematical operators^193,195. It is noteworthy that nonlocal metasurfaces are specialized for implementing mathematical operators for analogue image processing. Kwon et al. suggested the basic differential operators using nonlocal metasurfaces, and showed the Laplacian operator can be implemented by combining 1D operators for analogue edge detection¹⁹⁶. Additionally, Kwon et al. proposed design strategies of polarization insensitive nonlocal metasurface for edge detection¹⁹⁷. Zhou et al. fabricated Laplacian operator metasurface based on photonic crystal slab, as well as demonstrated low-power and high-speed edge detection on biological cell samples with minimal optical elements.

Second-order spatial differentiation is a sophisticated mathematical procedure employed to ascertain the rate of change in the spatial gradient of a function^{182,184−186}. In image processing, this operation is pivotal for accentuating edges and distinct features by emphasizing regions where rapid intensity fluctuations occur. An advanced optical filter that functions as a Laplacian operator can execute the second-order spatial differentiation of the transmitted light characterized by a specific electric field profile. Consequently, the output is the second derivative of the initial image, which distinctly underscores the edges and salient features of the image [Fig. 5(b)]¹⁸⁷.

Differential interference contrast (DIC) microscopy is another example of label-free imaging of transparent samples^198,199. DIC microscopy visualizes subtle differences in the thickness or refractive index variations in phase objects such as transparent cells or intracellular structures²⁰⁰. However, conventional anisotropic DIC (a-DIC) microscopy requires mechanical rotation of the prism to obtain isotropic differential images, making it unsuitable for rapid imaging of live specimens^201,202. Wang et al.¹⁹ overcame this limitation by employing a single-layer metasurface for isotropic DIC (i-DIC) imaging, which is not available with conventional optical elements. This represents a key component of next-generation imaging technology capable of precisely visualizing minute structural details in transparent samples. The metasurface plays a crucial role in modulating the optical properties, including polarization transformation and data alteration, and was designed to capture directionally invariant differential contrast in a single shot [Fig. 5(e)]¹⁹. The unique functionalities of metasurfaces stem from their intricate nanostrucatural designs. They have potential applications in biomedical imaging by harnessing the compactness and functionalities of metausrfaces, driving a cascade of ongoing research endeavors.

Tunable metasurfaces

$Figure 6. Various tunable metasurfaces and representative working principles. (a) A liquid crystal cells combined electrically tunable edge-detection metasurface. Scale bar: 5 μm. (b) Stretchable zoom metasurface fabricated on elastic substrate. (c) A MEMS combined varifocal metasurface. The focal length can be controlled by adjusting the distance be-tween two lenses using MEMS. (d) A varifocal metasurface consists of thermally responsive material that deforms in its crystalline state under heating, thereby causing a change in refractive index. Figure reproduced with permission from: (a) ref.122, American Chemical Society; (b) ref.210, American Chemical Society; (c) ref.214, Springer Nature; (d) ref.112, Springer Nature.$

Figure 6. Full-Size Img PowerPoint

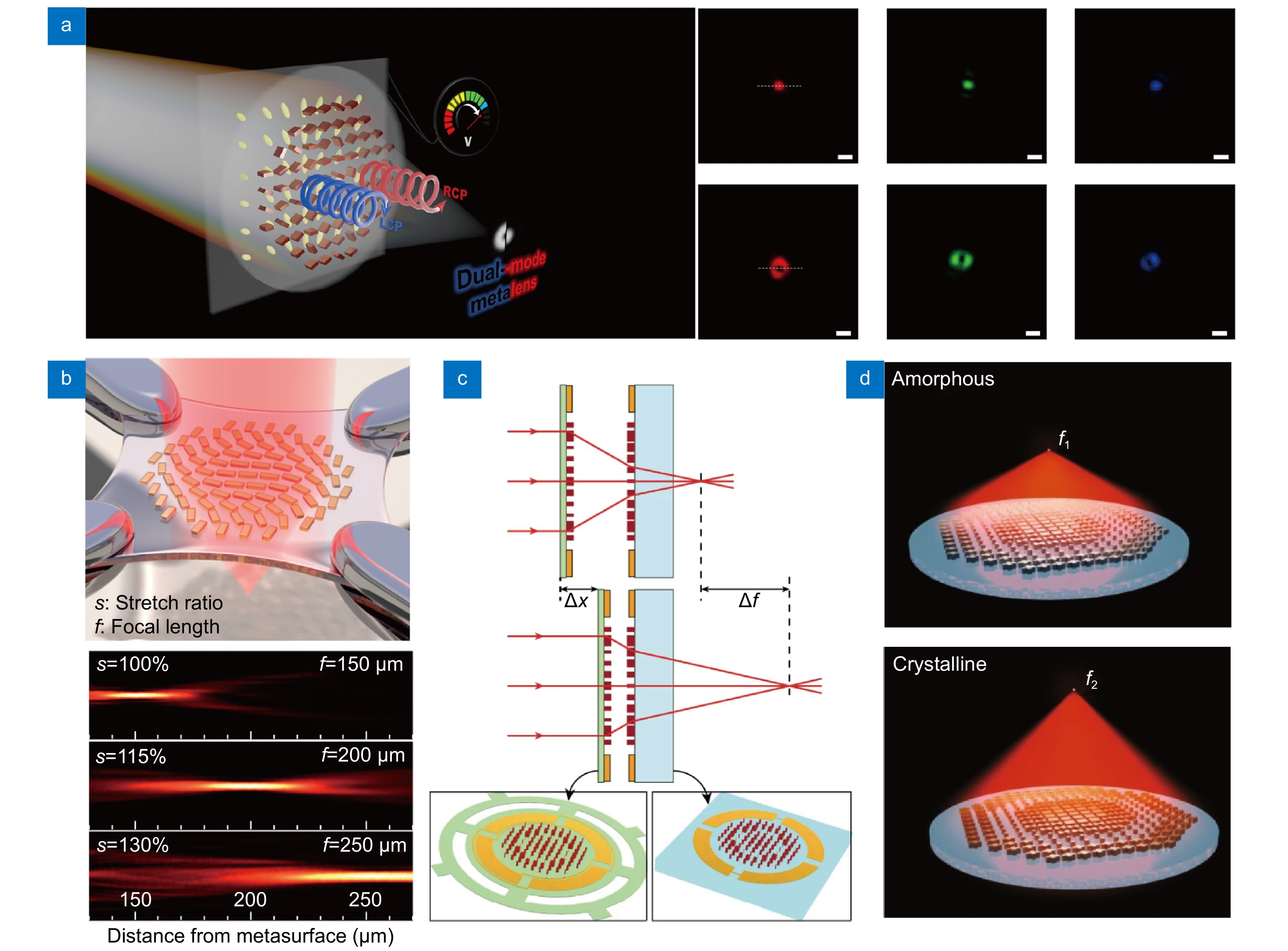
Various tunable metasurfaces and representative working principles. (a) A liquid crystal cells combined electrically tunable edge-detection metasurface. Scale bar: 5 μm. (b) Stretchable zoom metasurface fabricated on elastic substrate. (c) A MEMS combined varifocal metasurface. The focal length can be controlled by adjusting the distance be-tween two lenses using MEMS. (d) A varifocal metasurface consists of thermally responsive material that deforms in its crystalline state under heating, thereby causing a change in refractive index. Figure reproduced with permission from: (a) ref.¹²², American Chemical Society; (b) ref.²¹⁰, American Chemical Society; (c) ref.²¹⁴, Springer Nature; (d) ref.¹¹², Springer Nature.

Correlative imaging across various imaging modalities (i.e., combining bright field and edge-detection mode) is often required to unveil complex biological processes. However, complexity of optical setup restricts the implementation of combining different imaging modalities. Thus, tunable optics are preferred for constructing correlative imaging systems, as they can minimize the physical vibration and perturbations during mode switching. Metasurfaces also have emerged as strong candidates for tunable imaging system owing to their thin nature and abundant design flexibility. Switching modes of metasurfaces can be achieved in several ways, including electrical, mechanical (e.g., stretching), and stimuli-responsive (e.g., thermal) methods. In this section, tunable metasurfaces are comprehensively discussed.

Liquid crystal (LC) cell is the most representative tools for realization of electrically tunable metasurfaces. Their anisotropic refractive index and responsiveness to electric fields enable effective modulation of optical phases^203−206. Consequently, metasurfaces combined with LC cell function as electrically tunable lens by applying an electric field, like liquid crystal display (LCD)^206−208. As demonstrated by Badloe et al.¹²² in 2023, this technique was used to switch between bright-field and edge-detected modes within a few microseconds, allowing the seamless correlative imaging of transparent cells [Fig. 6(a)]. The integration of LC with metasurfaces eliminates the need for additional devices for mode changing and offers substantial benefits in terms of miniaturization and correlative imaging. This type of mode changing also can be conducted through physical distortion of metasurfaces^209,210. The metasurfaces fabricated on an elastic material can be easily deformed under an applied force, modifying the meta-atom period, and resulting in the distortion of the wavefront [Fig. 6(b)]. Sophisticated reshaping of metasurfaces allows the mode changing, but this requires complex device such as microelectromechanical systems (MEMS) for fast and reproducible mode control^211−213. Arbabi et al.²¹⁴ demonstrated a MEMS-integrated varifocal metasurface that adjusts the distance between two metasurfaces [Fig. 6(c)]. Another example is the work by Luo et al.²¹⁵ who achieved a tunable metasurface using a moiré metalens composed of cascaded phase plates with complementary phase profiles. This structure adjusts the focal length not by changing the distance between two metalenses, but by modifying the mutual angle of the cascades, which can be advantageous for ultra-thin systems. Phase-change materials, which undergo changes in physical properties in response to external stimuli (e.g., thermal expansion or phase transition^{112,216−218}), are also potential candidates for tunable systems. Song et al.²¹⁹ utilized VO₂ to achieve a tunable lens that can switch between dual-focus, single-focus, and no-focus modes at a wavelength of 4 μm through temperature control. They also accomplished opposite circular polarization conversion and adjustable focusing. Another example, Shalaginov et al.¹¹² showcased an varifocal metasurface by adopting phase change material GSST that deform in crystalline state under thermal annealing [Fig. 6(d)]. This tunable varifocal metasurface operates at a wavelength of 5.2 μm and exhibits a significant refractive index contrast between the amorphous and crystalline states of GSST. GSST offers the advantage of broadband transparency in the infrared region in both states.

Metasurfaces for tissue and animal imaging applications

Optical microscopy is an indispensable tool for imaging biological sampels²²⁰. With the increasing demand for complex structures and large-field imaging of animal tissue, advanced optical imaging techniques have attracted increasing attention. Notably, along with the development of fluorescent protein engineering and hardware, fluorescence imaging has emerged as the gold standard for biological imaging. Concurrently, advanced optical microscopy has also been developed to fully utilize fluorescent techniques such as confocal, light-field, light-sheet, super-resolution microscopy, fluorescence correlation spectroscopy (FCS), and ultrafast imaging techniques^221−223. In addition, various optical imaging modalities that do not require fluorescent labeling also have been developed, including optical coherence tomography (OCT), photoacoustic, phase contrast, polarization, dark field, and holographic imaging^224−228.

Although these techniques exhibit superior performance, they require expensive and bulky hardware and careful maintenance. Integrating multiple functions into a limited space requires considerable cost and effort to precisely maintain and align the systems. Metasurfaces have received increasing attention as alternative solutions to address these issues. The multifunctionality and thin nature of metasurfaces enable the combination of multiple optical elements into a single flat component, resulting in significant system simplification. In this section, conventional optical imaging methods specialized for animal and tissue imaging are introduced and explored to understand their potential replacement by metalsurfaces.

Fluorescent microscopy

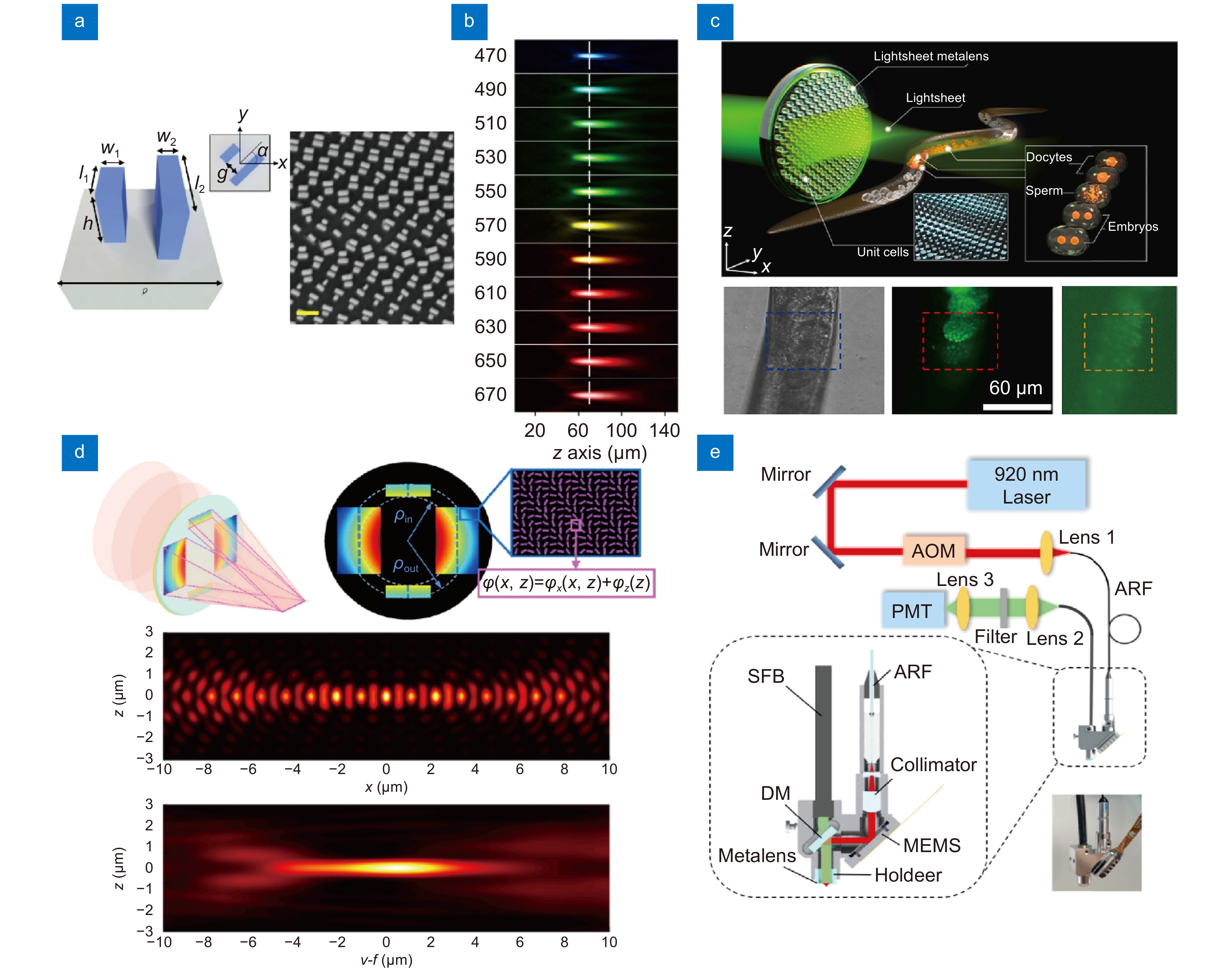
As the demand for fast and large-field imaging has increased in the field of biology, various types of advanced fluorescent microscopies are under development. Among them, light-sheet microscopy is particularly promising owing to its efficiency and fast imaging speed^229−231. Metasurfaces are potential candidates for reducing the complexity of conventional light-sheet microscopy systems because they allow easy modulation of the illumination profile. In addition, light-sheet microscopy is relatively free from chromatic aberration because the excitation and emission paths are separated. Luo et al.²¹ demonstrated the feasibility and performance of a metasurfaces-based light sheet microscope [Fig. 7(c)]²¹. Among the various types of light-sheet microscopes, the lattice light-sheet microscope, first developed by Chen et al.²³⁰ has demonstrated superior axial resolution (~370 nm) and out-of-focus background suppression compared with conventional microscopes. However, it should be noted that the optical setup for the lattice light-sheet microscope is highly complex. Metasurface-based lattice-light-sheet illumination can significantly simplify the system. According the simulation, metasurface results in an approximately 3-fold larger illumination area compared to a conventional lattice light-sheet microscope [Fig. 7(d)]^20,230. In a recent study, a metasurface-based Bessel beam lattice was implemented and applied to record neural activity²³². The use of metasurfaces greatly simplifies the system complexity, resulting in easier maintenance and alignment.

Fluorescence is the process of emitting light with a longer wavelength after absorbing light with a shorter wavelength and is known as the Stokes shift. Because of its broadband spectrum, fluorescence imaging typically involves optical components designed for wide spectrum. While currently available conventional achromatic lenses exhibit superior performance in correcting chromatic aberrations, compensating for chromatic aberrations remains a challenge for metasurfaces³⁹. To implement metasurfaces suitable for broadband fluorescent imaging, the aberration issues should be addressed. The most basic approach for implementing achromatic metasurfaces involves adjusting the group delay and group delay dispersion of light by modifying the dimensions and structures of the unit cells^50,51,235. Notably, Chen et al.¹² reported a broadband achromatic metasurfaces operating within the visible range that independently and precisely controlled the group dispersion and phase delay using a pair of nanofins [Fig. 7(a, b)]. Owing to the physical limitations of the metasurface design, computational image processing has emerged as promising strategies for correcting chromatic aberration. Classical deconvolution methods, such as the Wiener algorithm and optimization already have demonstrated the feasibility of computational correction^236−238. Furthermore, with recent advancements in deep learning, convolutional neural networks (CNN) have been widely used for aberration correction as well as automated optimization of metasurfaces, showing extremely high-quality post-processing^239,240. The development of these techniques has established a technical foundation for broadband fluorescent imaging using metasurfaces.

Another important microscopic technique in the biological field is multiphoton microscopy for deep-tissue imaging using a femtosecond laser in the near-infrared range. However, designing a metasurfaces for multiphoton fluorescence microscopy is challenging because of the larger difference between the excitation and emission wavelengths compared with single-photon microscopy. By utilizing the multifunctionality of metasurfaces, Arbabi et al.²³³ realized a metasurface for two-photon microscopy by separating the excitation and emission phase profiles with polarization dependency. Metasurfaces are also suitable for miniaturized optical microscopes used in vivo neural recordings in freely behaving rodents. The miniaturized head-mounted microscopy enables the capture of neural activity from freely behaving rodents to correlate the brain signal with animal motion. However, in the case of mice, total weight of the head-fix microscope should be less than 15% (<4 g) of the body weight to allow free movement²³⁴. The weight of conventional optics interrupts the behavior of rodents and may result in artifacts in recorded neuronal signals. Wang et al.²² developed a miniaturized two-photon microscope with only ~1.36 g of weight using a metasurface [Fig. 7(e)]. They obtained neuronal image from transgenic mouse up to a cortical depth of 70 µm with nearly diffraction-limited lateral resolution (~0.92 µm of lateral, ~18.08 µm of axial resolution) at 920 nm of wavelength.

Figure 7. Full-Size Img PowerPoint

Various metasurfaces-derived fluorescent microscopies for animal imaging applications. (a) Geometry and structural parameters of unit cell consist of paired nanofins for achromatic metasurface. Scale bar: 500 nm. (b) PSF of achromatic metasurface at various wavelength. The focal plane (dotted line) coincides regardless of the wavelength. (c) Illustration of metasurface-based light sheet microscopy (top), along with a bright-field, light sheet fluorescent microscopy, and wide-field fluorescence image of C. elegans (bottom). (d) The complex phase profile of metasurface for lattice light-sheet and its PSF. (e) Miniaturized two-photon microscopy incorporating a metasurface. Figure reproduced with permission from: (a), (b) ref.¹², Springer Nature; (c) ref.²¹, De Gruyter; (d) ref.²⁰, De Gruyter; (e) ref.²², American Chemical Society.

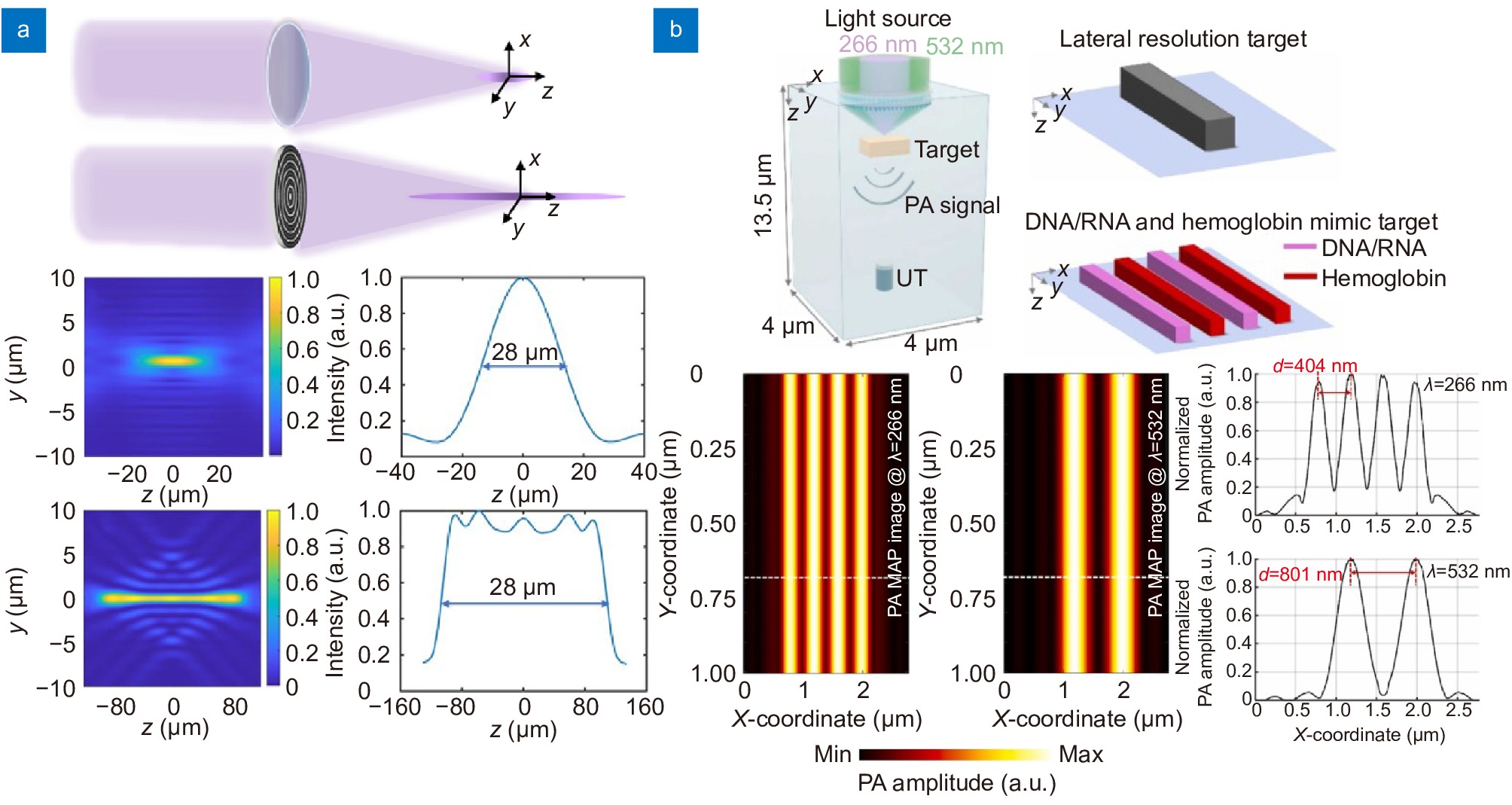
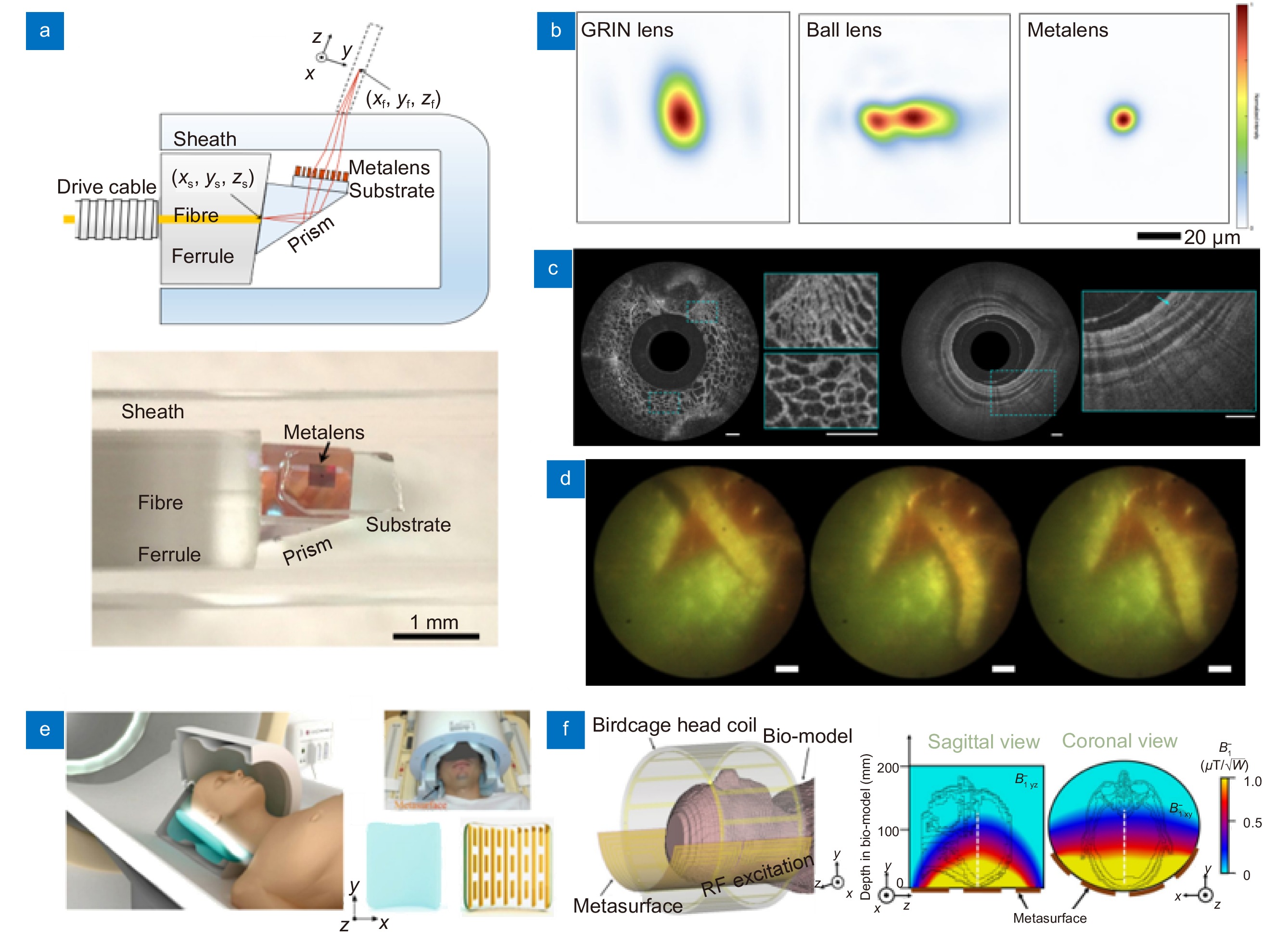
Photoacoustic microscopy (PAM)

Extending DOF significantly increases the clear imaging volume, as the PAM acquires an ultrasound signal in the vertical direction. Although Bessel beams are commonly employed to increase the DOF, their low efficiency and the need for additional optical elements are obstacles to high-quality imaging. Song et al.²⁴⁴ developed PAM using a metasurface-based needle-like beam to extend the DOF, thereby increasing the clear imaging volume [Fig. 8(a)]. The enhanced DOF also minimizes out-of-focus image blurring in unprocessed tissues with uneven surfaces for label-free histological imaging. These features make it suitable for intraoperative label-free histological imaging and virtual staining, in which reducing the staining time is important. Another metasurface application of PAM is in multichannel imaging. Dual-channel imaging at the UV and visible wavelengths is required for PAM imaging to observe multiple objects, such as DNA/RNA and vascular-related disorders simultaneously. However, UV-visible dual-channel imaging is hindered by chromatic aberrations resulting from large gaps in wavelengths. To correct this problem, a hafnium oxide multilayered metasurface compatible with the UV-visible range was proposed for photoacoustic imaging in a simulation [Fig. 8(b)]²³. This specially designed metasurface, 1.4 µm thick with a high NA of 0.8, outperforms commercially available UV-visible lenses, which typically have NA of 0.5. The combination of metasurfaces and PAM is suitable for clinical applications that require miniaturized and high-performance systems for imaging in narrow spaces. It is worth noting that photoacoustic endoscopy is quite effective in detecting gastric cancer and inflammation²⁴⁸. Several studies have been conducted to integrate compact and high-resolution optics with intravascular photoacoustic and ultrasound imaging systems⁷⁶. We anticipate that the integration of metasurfaces into PAM will introduce new opportunities for ultracompact, high-performance, and multispectral applications of PAM in biological imaging.

Figure 8. Metasurface-based PSF engineering for photoacoustic microscopy applications. (a) A comparison of PSF between a conventional objective lens with a NA of 0.13 and a metasurface designed for extended depth of focus at UV wavelength. The objective lens has a depth of focus of 28 µm, whereas the metasurface has a depth of focus of 216 µm. (b) Optical setup for dual-channel PAM using a UV-Visible metasurface (top). PAM imaging simulation and resulting intensity profiles of phantom at UV and visible light (bottom). Figure reproduced with permission from: (a) ref.244, Optical Society of America; (b) ref.23, Elsevier.

Figure 8. Full-Size Img PowerPoint

Metasurface-based PSF engineering for photoacoustic microscopy applications. (a) A comparison of PSF between a conventional objective lens with a NA of 0.13 and a metasurface designed for extended depth of focus at UV wavelength. The objective lens has a depth of focus of 28 µm, whereas the metasurface has a depth of focus of 216 µm. (b) Optical setup for dual-channel PAM using a UV-Visible metasurface (top). PAM imaging simulation and resulting intensity profiles of phantom at UV and visible light (bottom). Figure reproduced with permission from: (a) ref.²⁴⁴, Optical Society of America; (b) ref.²³, Elsevier.

Photoacoustic microscopy (PAM) is an innovative imaging approach, overcoming the limitation of the penetration depth of light in scattering media by harnessing acoustic signals^225,241. The underlying mechanism of this technique is photoacoustic effect, which converts the absorbed light into acoustic waves through thermal expansion. As attenuation of acoustic signal is lower than that of light signals in tissue, imaging in deeper tissue is permitted. Depending on the illumination strategy, they can be classified as optical-resolution photoacoustic microscopy (OR-PAM) and acoustic-resolution photoacoustic microscopy (AR-PAM). Typically, the penetration depth of OR-PAM and AR-PAM reaches up to ~1 mm and several centimeters, with 0.4-5 µm and >40 µm of lateral resolution, respectively^23,242−247. Notably, elaborate PSF engineering could significantly enhance the image quality for OR-PAM, given its utilization of focused light. Recent studies have employed metasurfaces for system improvement owing to their design flexibility.

Metasurfaces for human applications

This chapter discusses innovative idea of metasurfaces for human applications. From medical devices and biometrics, metasurfaces have enhanced the resolution, sensitivity, and diversity of devices for human applications, such as endoscopic imaging, MRI, 3D facial recognition and fingerprint imaging. This chapter explores into the innovative potential of metasurfaces on devices for human applications.

Endoscopic imaging

As mentioned previously, the ability of metasurfaces to control the properties of light enables more accurate diagnostics that are not possible using traditional fiber-optic catheters. Endoscopic imaging using a metasurface, which is sensitive to polarization, allows for a clearer distinction of the surrounding tissues compared to traditional fiber-optic endoscopes^258−260. Endoscopy using optical fibers integrated with metasurfaces is expected to enable a wide range of applications in bioimaging and clinical fields, including real-time biopsies, cancer diagnostics, and high-resolution in vivo medical imaging. Additionally, integrating metasurfaces with deep learning can reduce the overall imaging processing time and quickly obtain high-resolution tomographic images²⁶¹. This integration enables real-time processing, high-resolution image acquisition, and non-invasive diagnostics in bioimaging using metasurfaces²⁶².

Endoscopy is an optical imaging technique used to visually inspect internal organs. This technology has become an essential tool for acquiring minimally invasive organ images, particularly by using high-resolution fiber-optic systems^249,250. OCT is another imaging technique utilized for acquiring cross-sectional views of biological tissues, providing detailed features of the microstructure with high-resolution (1–15 μm). The combination of these technologies is considered a valuable tool for the identification, diagnosis, and monitoring of diseases, particularly eye conditions such as glaucoma. Additionally, when combined with a catheter, it aids in the diagnosis of internal organ diseases such as vascular and gastrointestinal disorders. However, traditional endoscopy encounters significant limitations owing to optical aberrations and the trade-off between transverse resolution, depth of focus and penetration depth^251−254. To overcome these limitations, metasurfaces have attracted considerable interest because of their light modulation ability^3,10,255.

Figure 9. Biomedical applications of metasurfaces. (a) Schematic (top), and distal end of the nano-optic endoscope using ultra-thin metasurface. (b) Comparison of PSF at a wavelength of 1310 nm for an OCT catheter based on GRIN, ball, and metasurface, respectively. The metasurface-based OCT catheter shows the clearest PSF. (c) The image of fruit flesh of grape (left) and swine airway (right) obtained from the metasurface-based nano-optic endoscope. Scale bar: 500 μm. (d) Full color video rate imaging of caterpillar on a strawberry leaf taken from meta-optical fiber endoscope. Scale bar: 500 μm. (e) Illustration of MRI scanning with metasurface made of a high permittivity dielectric pad and metal stripes. (f) Schematic and simulation results of metasurface assisted MRI scanning. Homogeneous magnetic field enhancement is observed. Figure reproduced with permission from: (a–c) ref.25, Springer Nature; (d) ref.257, Springer Nature; (e) ref.26, Springer Nature; (f) ref.263, Springer Nature.

Figure 9. Full-Size Img PowerPoint

Biomedical applications of metasurfaces. (a) Schematic (top), and distal end of the nano-optic endoscope using ultra-thin metasurface. (b) Comparison of PSF at a wavelength of 1310 nm for an OCT catheter based on GRIN, ball, and metasurface, respectively. The metasurface-based OCT catheter shows the clearest PSF. (c) The image of fruit flesh of grape (left) and swine airway (right) obtained from the metasurface-based nano-optic endoscope. Scale bar: 500 μm. (d) Full color video rate imaging of caterpillar on a strawberry leaf taken from meta-optical fiber endoscope. Scale bar: 500 μm. (e) Illustration of MRI scanning with metasurface made of a high permittivity dielectric pad and metal stripes. (f) Schematic and simulation results of metasurface assisted MRI scanning. Homogeneous magnetic field enhancement is observed. Figure reproduced with permission from: (a–c) ref.²⁵, Springer Nature; (d) ref.²⁵⁷, Springer Nature; (e) ref.²⁶, Springer Nature; (f) ref.²⁶³, Springer Nature.

Pahlevaninezhad et al.²⁵ successfully obtained high-resolution images with an adequate imaging depth of focus using a metasurface for endoscopic OCT system[Fig. 9(a)]. The use of metasurfaces allows for focus with smaller astigmatism compared to traditional lenses, such as gradient-index (GRIN) lenses or ball lenses [Fig. 9(b)]. The effective depth of focus reached was 211 µm (tangential) and 315 µm (sagittal), surpassing the expected 90 µm from an achromatic lens with the same NA²⁵. They successfully navigated the challenges related to optical aberrations and the compromise between the lateral resolution and depth of focus, obtaining high-resolution images of the internal organs [Fig. 9(c)]. Pahlevaninezhad et al.²⁵⁶ also developed large depth of focus (1.25 mm) tomography maintaining high-resolution (~3.2 µm @1300 nm) in three dimensions. Because of the balance required between the depth of focus and the lateral resolution, which depends on the NA, the group segregated this relationship using metasurface-derived bijective illumination. The overall PSF of the bijective metasurface, shaped by multiplying the illumination and collection PSF, displayed a precise form at the focal line where the two PSFs converged. Although they did not implement a miniaturized endoscopic system, they suggested the possibility of a metasurface-based miniaturized endoscope with superior performance²⁵⁶. Fröch et al.²⁵⁷ studied a meta-optical fiber endoscope capable of real-time full-color imaging [Fig. 9(d)]. This research utilized the characteristics of a metasurface not only to provide color imaging across the entire visible spectrum but also to achieve a 33% reduction in the length of the rigid tip compared to traditional GRIN lenses.

Magnetic resonance imaging (MRI)

Schmidt et al.²⁶ recently developed an innovative metasurface structure to enhance the performance of ultra-high-field MRI scanners [Fig. 9(e)]. This newly designed metasurface consists of a two-dimensional metasurface combined with a dielectric substrate with a high dielectric constant. The primary goal of this structure is to improve the local functionality of the MRI scanners. Notably, this is the first metasurface that can be integrated with closely fitted receiving-coil arrays that are commonly used in clinical MRI scans. This compact and flexible resonant structure has great potential for advancing MRI technology. Furthermore, in another study, the implementation of a 1.5 T MRI scanner with a flexible metasurface enabled the detailed imaging of body parts according to the body curvature [Fig. 9(f)]²⁶³. These studies demonstrate that enhancing the MRI performance with metasurfaces can pave the way for faster and more accurate diagnostics and treatment decision-making.

MRI is an advanced medical imaging technology that has evolved over nearly 50 years and can visualize a wide range of anatomical structures such as the brain, spine, muscles, joints, organs, and blood vessels. It offers exceptional contrast for soft tissues, enabling the diagnosis of neurological disorders, musculoskeletal conditions, cardiovascular diseases, and cancer^264,265. One of the primary advantages of MRI is that it is non-invasive and does not use a high-energy radiation beam, making it safer than X-rays or CT scans. However, the current MRI technology is limited by its low spatial resolution. Most MRI machines used for medical purposes operate at magnetic strengths of 1.5 T or 3 T²⁶⁶, typically achieving a resolution of approximately 1.5×1.5×4 mm³. A common approach for increasing the spatial resolution is to use a stronger magnetic field, which can potentially have negative effects on the human body and result in image distortion²⁶⁷.

The use of metasurfaces has been proposed as a solution to enhance MRI resolution without a stronger magnetic field. A metasurface can resonantly enhance the strength of a magnetic field and spatially redistribute it by increasing the coupling between radio-frequency coils in specific areas²⁶⁸. Additionally, owing to their thin and flat characteristics, the use of metasurfaces in MRI allows closer placement in the patient and between the receiving coil arrays, offering several advantages^269,270. For example, by integrating a metasurface within 1.5 T MRI scanners, the deployment of a metallic wire array facilitates the controlled manipulation of the radio-frequency electromagnetic field at a subwavelength scale, significantly amplifying local magnetic fields. This enhances the SNR by a factor of ~2.7, enabling the acquisition of higher-resolution images in a shorter time^269,271. Similarly, various studies have been conducted using metasurfaces to reduce MRI scanning times and improve the SNR^26,272.

Devices for facial recognition

Traditional facial recognition has been studied for auxiliary communication, mental health and emotion monitoring, pain assessment, and the interpretation of facial nuances^273−277. However, biometric authentication is a more practical application^278,279. This technology has already been widely utilized in smartphones to unlock devices and make payments²⁸⁰. This has brought convenience to daily life; however, the need for more accurate recognition has been increasingly highlighted in terms of security. For this reason, facial recognition has been adopted not only for 2D imaging but also for 3D depth imaging. Light-field cameras and dot projections are typically used for 3D depth encoding.

Figure 10. Representative metasurface integrated devices for biometric applications. (a) Implementation of 3D facial depth sensing using a point cloud generating metasurface. (b) Illustration of a metasurface-based dot projector combined with PCSEL, which is 233 times smaller than a commercial DOE-based dot projector. (c) Schematic of metasurface-based device for fingerprint recognition (left) and fingerprint image obtained by the device. (d) Fingerprint image obtained using a metasurface array imaging device. The array structure enables the acquisi-tion of clearer and wider fingerprint images. Figure reproduced with permission from: (a) ref.49, Springer Nature; (b) ref.28, American Chemical Society; (c) ref.27, American Chemical Society; (d) ref.283, De Gruyter.

Figure 10. Full-Size Img PowerPoint

Representative metasurface integrated devices for biometric applications. (a) Implementation of 3D facial depth sensing using a point cloud generating metasurface. (b) Illustration of a metasurface-based dot projector combined with PCSEL, which is 233 times smaller than a commercial DOE-based dot projector. (c) Schematic of metasurface-based device for fingerprint recognition (left) and fingerprint image obtained by the device. (d) Fingerprint image obtained using a metasurface array imaging device. The array structure enables the acquisi-tion of clearer and wider fingerprint images. Figure reproduced with permission from: (a) ref.⁴⁹, Springer Nature; (b) ref.²⁸, American Chemical Society; (c) ref.²⁷, American Chemical Society; (d) ref.²⁸³, De Gruyter.

Structured light-based facial depth encoding techniques have been adopted in smartphones for device unlocking and biometric payment systems. Conventional facial recognition modules often employ vertical cavity surface-emitting lasers (VCSEL) as structured light sources owing to their low power consumption. The integration of metasurfaces with VCSEL has been proposed for more power-efficient and arbitrary light modulation²⁸². Moreover, recent research has been conducted on depth perception and facial recognition using structured light with a photonic crystal surface-emitting laser (PCSEL), which is more compact and reduces power consumption compared to VCSEL [Fig. 10(b)]. The PCSEL-integrated metasurface system achieved a form factor approximately 233 times smaller than that of DOE-based dot projection modules. Additionally, it exhibits better performance than previous methods in terms of the number of dots, angular field of view, area, and sampling rate²⁸. The use of metasurfaces for facial recognition not only significantly contributes to device miniaturization but also has the potential to reduce power consumption and enhance performance. Owing to these benefits, biometric recognition methods using metasurfaces can be widely employed in potent security systems.

Metasurfaces are considered promising components for dot projection-based 3D depth encoding devices owing to their simplicity and ability to generate an enormous number of point clouds^{28,49,281,282}. The generation of numerous dot arrays for dense sampling over a wide angle is important for the precise acquisition of facial contours. In 2018, Li et al.²⁸¹ reported a metasurface capable of generating 4044 random points over a 90° angle, addressing the drawbacks of diffractive optical elements (DOE), such as the difficulty of depth-controlled fabrication and large thickness. Kim et al.⁴⁹ fabricated a dense dot array generating metasurface (~10 K) covering a wider angle (180°) [Fig. 10(a)]. As a proof of principle, they reconstructed a 3D depth map of a facial mask even when it was placed at a 50° angle from the optical axis.

Devices for fingerprint recognition

Recently, there has been an increasing demand for fingerprint recognition, particularly for its integration into handheld devices such as smartphones, driving continuous advancements in technology. To satisfy these increasing demands, the use of metasurfaces has led to significant advancements over traditional methods. This enables the creation of compact, high-resolution, and sensitive optical systems, significantly enhancing their applicability in security and personal authentication. Metasurfaces are particularly suitable for large-field imaging over short distances, such as fingerprint imaging. Quadratic phase metasurface imaging systems, with their wide FOV (~100°) and ability to capture the fine patterns with high precision (~100 µm), can offer a compact and reliable method of fingerprint authentication [Fig. 10(c)]²⁷. In addition, the use of a metasurface array can reduce the thickness of the sensing module (~1 mm) while enabling clear fingerprint imaging [Fig. 10(d)]²⁸³. The miniaturization of these systems not only contributes to the reduction in the size and cost, but also offers a much simpler and more efficient solution compared to conventional methods. Therefore, the development and research of metasurface-based fingerprint recognition technology are expected to continue, leading to progress in the field of biometric authentication.

Biometric fingerprint recognition is a robust security mechanism that utilizes the unique fingerprint patterns of individuals for identity verification. The journey of fingerprint recognition commenced in England in 1684, when Grew discovered the uniqueness of people's fingerprints²⁸⁴. Fingerprints can be distinguished uniquely based on intricate ridge patterns on the fingertips²⁸⁵. In addition, the enduring nature of fingerprints, which remain consistent from birth and rapidly regenerate even after alterations caused by external factors, underscores their reliability in identification²⁸⁵. This specificity and invariance render fingerprint recognition one of the most longstanding and trusted biometric technologies for personal identification^286−288. Fingerprint recognition offers significant advantages in terms of security, as it is resistant to forgery and cannot be lost^289,290.

Conclusions and future perspectives

Despite these limitations, leveraging the advantages of metasurfaces can significantly enhance the performance in bioimaging, making them a promising technology. Among their various merits, we would like to highlight three key advantages of metasurface for bioimaging. First, metasurfaces are highly specialized for PSF engineering, which offers significant benefits for scanning type microscopes. If strong illumination, generally available for scanning type microscope, is given, it can compensate for the low efficiency of metasurfaces. Furthermore, data acquisition using scanning methods enlarges imaging field of view and reduces aberrations. Indeed, this is well demonstrated in previous studies such as PAM²³, and SOL based super-resolution fluorescent microscopy¹²⁷. The second advantage is compatibility with automatic differentiation, which enables the simultaneous optimization of entire system with metasurfaces. In many cases, performance of metasurfaces can be simulated using the scalar diffraction theory, which is based on Fourier transform. This simulation can be effectively integrated with gradient backpropagation methods and deep learning, resulting in metasurfaces being optimized to simultaneously improve both the model’s performance and the optical system. This approach, known end-to-end optimization, can be applied to various applications. For instance, Tseng et al. developed a deep learning model for correcting chromatic aberration and combined it with metasurfaces designer, resulting in the optimized metasurface that enhance the performance of the deep learning model²³⁹. This approach paves the way for creating customized systems tailored for specialized applications. Lastly, system miniaturization is a promising application of metasrufaces. The thickness of optical components and the required free space for light propagation are significant obstacles for compressing optical systems. While the thin nature of metasurfaces addresses the thickness issue, reducing the propagation space remains a challenge. Notably, nolocal metasurfaces¹⁹⁷ have gained attention as a potential solution for this problem. Indeed, several studies have demonstrated space compression using nonlocal metasurfaces that operate directly in momentum domain¹⁹⁶. This capability enables the creation of compact and miniaturized optical systems, facilitating the development of more compact hybrid systems that integrate various types of microscopes^95,234. By combining these technologies, more precise and efficient imaging can be achieved.

Although metasurfaces appear to be promising tools, three major limitations and challenges need to be addressed for them to replace, or at least be used alongside, conventional optics. First, current metasurface-based imaging systems suffer from aberrations and efficiency issues. These problems degrade image quality and hinder the accurate collection of biological data. Additionally, the small metasurfaces require additional topcail system for magnification. Imaging through current metasurfaces has lower light efficiency and higher aberrations compared to traditional lenses. For instance, fluorescence imaging, which is gold-standard for bioimaging, requires a sensitive detection system due to its poor efficiency, and light collection efficiency of metasurfaces is not adequate. Efforts are being made to resolve these issues through computational methods. Recent image processing techniques based on deep learning offer impressive correcting performance. Additionally, advanced inverse design methods enables the development of high-efficiency metasurfaces^239,240. Second, there is the challenge of manufacturing. Mass production of large and diverse metasurfaces remains difficult. Existing metasurfaces face inefficiencies in terms of size and fabrication cost. High-performance bioimaging often requires specialized systems tailored to specific imaging subjects, species and environments. For example, miniaturized microscopes or endoscopes are necessary for in vivo imaging of animal. Super-resolution microscopy is required for imaging subcellular structures of biosamples^15,152, and MRI remains the only method for measuring whole brain activity of live humans. Therefore, a variety of metasurfaces need to be produced in large quantities to meet the demands of different imaging fields. While conventional optical elements benefit from well-established mass production platforms, most metasurfaces currently rely on e-beam lithography, which has low in productivity. To address this, various approaches, such as nanoimprint lithography²⁹¹, have been studied to improve the productivity of high-performance metasurfaces. Lastly, the development of advanced materials is crucial for achieving high-quality bioimaging. Current metasurfaces are often optimized for infrared wavelength. While infrared light has been adopted in some bioimaging applications, visible spectrum remains the most widely used for this purpose. Silicon nitride, for example, is frequently used for visible metasurfaces due to its transparency, but its low refractive index restricts the design flexibility and complicates the fabrication (e.g., high aspect ratio meta-atoms). TiO₂ offers good refractive index and excellent transparency but requires hard fabrication process such as atomic layer deposition. Therefore, developing advanced materials enables design capabilities and simplify the fabrication process.

Although still in the early stages, the integration of metasurfaces with biological imaging holds the potential to revolutionize the field. The synergy between metasurfaces and advanced imaging techniques promises to enhance the performance and capabilities of imaging systems, introducing novel functionalities that are unattainable with traditional optical components. In the future, we anticipate that metasurfaces will play a pivotal role in various imaging applications, including real-time diagnostics, high-resolution imaging, and non-invasive medical procedures. Continued research and development in optics, materials science, and image processing will expand the application boundaries of metasurfaces, establishing them as a cornerstone of next generation bioimaging technologies.

In this review, we have explored the principles of metasurface design and its comprehensive applications in the field of biological imaging. The remarkable features of metasurface, such as their multifunctionality, thinness, and compatibility with conventional optical systems, render them promising optical elements. Particularly in bioimaging, their potential to replace bulky and complex components with simpler, more efficient ones is noteworthy. To comprehensively cover the metasurfaces from basic principles to applications, we first discussed the principes of phase modulation of metasurfaces. Then, we have explored the representative classes of materials for creating metasurfaces depending on their properties. Particularly, dielectric materials and tunable materials are most widely used for bioimaging due to its compatibility within visible range and versatility. Furthermore, we showcased the broad applications of metasurface in biological field depending on the subject, such as cell, tissue, and human. The detailed categories include promising techniques for bioimaging, such as super-resolution^15,152, analog image processing^182,186, fluorescent imaging^20,21, PAM²³, endoscopy^25,257, MRI, and biometrics. Indeed, metasurfaces have widely utilized in these field and exhibited superior performance in particular aspects.

Acknowledgements

This study was financially supported by National Research Foundation (NRF) grants (RS-2023-00266110, NRF-2020R1A5A1019649, NRF-2022M3C1A3081312, and NRF-2023M3K5A109482011) funded by the Ministry of Science and ICT (MSIT) of the Korean government. I. Kim acknowledges the NRF Sejong Science Fellowship (NRF-2021R1C1C2004291) funded by the MSIT of the Korean government.

Competing interests

The authors declare no competing financial interests.

References (291)

References

[1]	Avrutsky I, Chaganti K, Salakhutdinov I et al. Concept of a miniature optical spectrometer using integrated optical and micro-optical components. Appl Opt 45, 7811–7817 (2006). DOI: 10.1364/AO.45.007811 CrossRef Google Scholar
[2]	Khorasaninejad M, Capasso F. Metalenses: versatile multifunctional photonic components. Science 358, eaam8100 (2017). DOI: 10.1126/science.aam8100 CrossRef Google Scholar
[3]	Khorasaninejad M, Chen WT, Devlin RC et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016). DOI: 10.1126/science.aaf6644 CrossRef Google Scholar
[4]	Ni XJ, Ishii S, Kildishev AV et al. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light Sci Appl 2, e72 (2013). DOI: 10.1038/lsa.2013.28 CrossRef Google Scholar
[5]	Kim I, Jang J, Kim G et al. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform. Nat Commun 12, 3614 (2021). DOI: 10.1038/s41467-021-23814-5 CrossRef Google Scholar
[6]	Kim I, Kim WS, Kim K et al. Holographic metasurface gas sensors for instantaneous visual alarms. Sci Adv 7, eabe9943 (2021). DOI: 10.1126/sciadv.abe9943 CrossRef Google Scholar
[7]	Paniagua-Dominguez R, Yu YF, Khaidarov E et al. A metalens with a near-unity numerical aperture. Nano Lett 18, 2124–2132 (2018). DOI: 10.1021/acs.nanolett.8b00368 CrossRef Google Scholar
[8]	Liang HW, Lin QL, Xie XS et al. Ultrahigh numerical aperture metalens at visible wavelengths. Nano Lett 18, 4460–4466 (2018). DOI: 10.1021/acs.nanolett.8b01570 CrossRef Google Scholar
[9]	Chung H, Miller OD. High-NA achromatic metalenses by inverse design. Opt Express 28, 6945–6965 (2020). DOI: 10.1364/OE.385440 CrossRef Google Scholar
[10]	Zhang SY, Wong CL, Zeng SW et al. Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective. Nanophotonics 10, 259–293 (2021). Google Scholar
[11]	Nguyen DD, Lee S, Kim I. Recent advances in metaphotonic biosensors. Biosensors 13, 631 (2023). DOI: 10.3390/bios13060631 CrossRef Google Scholar
[12]	Chen WT, Zhu AY, Sanjeev V et al. A broadband achromatic metalens for focusing and imaging in the visible. Nat Nanotechnol 13, 220–226 (2018). DOI: 10.1038/s41565-017-0034-6 CrossRef Google Scholar
[13]	Lin RJ, Su VC, Wang SM et al. Achromatic metalens array for full-colour light-field imaging. Nat Nanotechnol 14, 227–231 (2019). DOI: 10.1038/s41565-018-0347-0 CrossRef Google Scholar
[14]	Rho J, Ye ZL, Xiong Y et al. Spherical hyperlens for two-dimensional sub-diffractional imaging at visible frequencies. Nat Commun 1, 143 (2010). DOI: 10.1038/ncomms1148 CrossRef Google Scholar
[15]	Lee D, Kim YD, Kim M et al. Realization of wafer-scale hyperlens device for sub-diffractional biomolecular imaging. ACS Photonics 5, 2549–2554 (2018). DOI: 10.1021/acsphotonics.7b01182 CrossRef Google Scholar
[16]	Lee YU, Zhao JX, Ma Q et al. Metamaterial assisted illumination nanoscopy via random super-resolution speckles. Nat Commun 12, 1559 (2021). DOI: 10.1038/s41467-021-21835-8 CrossRef Google Scholar
[17]	Masuda S, Kuboki T, Kidoaki S et al. High axial and lateral resolutions on self-assembled gold nanoparticle metasurfaces for live-cell imaging. ACS Appl Nano Mater 3, 11135–11142 (2020). DOI: 10.1021/acsanm.0c02300 CrossRef Google Scholar
[18]	Huo PC, Zhang C, Zhu WQ et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett 20, 2791–2798 (2020). DOI: 10.1021/acs.nanolett.0c00471 CrossRef Google Scholar
[19]	Wang XW, Wang H, Wang JL et al. Single-shot isotropic differential interference contrast microscopy. Nat Commun 14, 2063 (2023). DOI: 10.1038/s41467-023-37606-6 CrossRef Google Scholar
[20]	Shi FH, Wen J, Lei DY. High-efficiency, large-area lattice light-sheet generation by dielectric metasurfaces. Nanophotonics 9, 4043–4051 (2020). DOI: 10.1515/nanoph-2020-0227 CrossRef Google Scholar
[21]	Luo Y, Tseng ML, Vyas S et al. Meta-lens light-sheet fluorescence microscopy for in vivo imaging. Nanophotonics 11, 1949–1959 (2022). DOI: 10.1515/nanoph-2021-0748 CrossRef Google Scholar
[22]	Wang CH, Chen QM, Liu HL et al. Miniature two-photon microscopic imaging using dielectric metalens. Nano Lett 23, 8256–8263 (2023). DOI: 10.1021/acs.nanolett.3c02439 CrossRef Google Scholar
[23]	Barulin A, Park H, Park B et al. Dual-wavelength UV-visible metalens for multispectral photoacoustic microscopy: a simulation study. Photoacoustics 32, 100545 (2023). DOI: 10.1016/j.pacs.2023.100545 CrossRef Google Scholar
[24]	Song W, Guo CK, Zhao YT et al. Ultraviolet metasurface-assisted photoacoustic microscopy with great enhancement in DOF for fast histology imaging. Photoacoustics 32, 100525 (2023). DOI: 10.1016/j.pacs.2023.100525 CrossRef Google Scholar
[25]	Pahlevaninezhad H, Khorasaninejad M, Huang YW et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat Photonics 12, 540–547 (2018). DOI: 10.1038/s41566-018-0224-2 CrossRef Google Scholar
[26]	Schmidt R, Slobozhanyuk A, Belov P et al. Flexible and compact hybrid metasurfaces for enhanced ultra high field in vivo magnetic resonance imaging. Sci Rep 7, 1678 (2017). DOI: 10.1038/s41598-017-01932-9 CrossRef Google Scholar
[27]	Lassalle E, Mass TWW, Eschimese D et al. Imaging properties of large field-of-view quadratic metalenses and their applications to fingerprint detection. ACS Photonics 8, 1457–1468 (2021). DOI: 10.1021/acsphotonics.1c00237 CrossRef Google Scholar
[28]	Hsu WC, Chang CH, Hong YH et al. Metasurface- and PCSEL-based structured light for monocular depth perception and facial recognition. Nano Lett 24, 1808–1815 (2024). DOI: 10.1021/acs.nanolett.3c05002 CrossRef Google Scholar
[29]	Yu NF, Genevet P, Kats MA et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011). DOI: 10.1126/science.1210713 CrossRef Google Scholar
[30]	Hu J, Bandyopadhyay S, Liu YH et al. A review on metasurface: from principle to smart metadevices. Front Phys 8, 586087 (2021). DOI: 10.3389/fphy.2020.586087 CrossRef Google Scholar
[31]	Yu NF, Capasso F. Flat optics with designer metasurfaces. Nat Mater 13, 139–150 (2014). DOI: 10.1038/nmat3839 CrossRef Google Scholar
[32]	Khorasaninejad M, Zhu AY, Roques-Carmes C et al. Polarization-insensitive metalenses at visible wavelengths. Nano Lett 16, 7229–7234 (2016). DOI: 10.1021/acs.nanolett.6b03626 CrossRef Google Scholar
[33]	Khorasaninejad M, Chen WT, Oh J et al. Super-dispersive off-axis meta-lenses for compact high resolution spectroscopy. Nano Lett 16, 3732–3737 (2016). DOI: 10.1021/acs.nanolett.6b01097 CrossRef Google Scholar
[34]	Mueller JPB, Rubin NA, Devlin RC et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys Rev Lett 118, 113901 (2017). DOI: 10.1103/PhysRevLett.118.113901 CrossRef Google Scholar
[35]	Cong LQ, Xu NN, Zhang WL et al. Polarization control in terahertz metasurfaces with the lowest order rotational symmetry. Adv Opt Mater 3, 1176–1183 (2015). DOI: 10.1002/adom.201500100 CrossRef Google Scholar
[36]	Chen XZ, Huang LL, Mühlenbernd H et al. Dual-polarity plasmonic metalens for visible light. Nat Commun 3, 1198 (2012). DOI: 10.1038/ncomms2207 CrossRef Google Scholar
[37]	Arbabi A, Horie Y, Bagheri M et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat Nanotechnol 10, 937–943 (2015). DOI: 10.1038/nnano.2015.186 CrossRef Google Scholar
[38]	Jiang SC, Xiong X, Hu YS et al. High-efficiency generation of circularly polarized light via symmetry-induced anomalous reflection. Phys Rev B 91, 125421 (2015). DOI: 10.1103/PhysRevB.91.125421 CrossRef Google Scholar
[39]	Huang LL, Chen XZ, Mühlenbernd H et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett 12, 5750–5755 (2012). DOI: 10.1021/nl303031j CrossRef Google Scholar
[40]	Moon SW, Lee C, Yang Y et al. Tutorial on metalenses for advanced flat optics: design, fabrication, and critical considerations. J Appl Phys 131, 091101 (2022). DOI: 10.1063/5.0078804 CrossRef Google Scholar
[41]	Luo WJ, Sun SL, Xu HX et al. Transmissive ultrathin pancharatnam-berry metasurfaces with nearly 100% efficiency. Phys Rev Appl 7, 044033 (2017). DOI: 10.1103/PhysRevApplied.7.044033 CrossRef Google Scholar
[42]	Fu X, Liang HW, Li JT. Metalenses: from design principles to functional applications. Front Optoelectron 14, 170–186 (2021). DOI: 10.1007/s12200-021-1201-9 CrossRef Google Scholar
[43]	Kim J, Li YM, Miskiewicz MN et al. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2, 958–964 (2015). DOI: 10.1364/OPTICA.2.000958 CrossRef Google Scholar
[44]	Wen DD, Yue FY, Li GX et al. Helicity multiplexed broadband metasurface holograms. Nat Commun 6, 8241 (2015). DOI: 10.1038/ncomms9241 CrossRef Google Scholar
[45]	Chen WT, Khorasaninejad M, Zhu AY et al. Generation of wavelength-independent subwavelength Bessel beams using metasurfaces. Light Sci Appl 6, e16259 (2017). Google Scholar
[46]	Xu R, Chen P, Tang J et al. Perfect higher-order Poincaré sphere beams from digitalized geometric phases. Phys Rev Appl 10, 034061 (2018). DOI: 10.1103/PhysRevApplied.10.034061 CrossRef Google Scholar
[47]	Jeon D, Shin K, Moon SW et al. Recent advancements of metalenses for functional imaging. Nano Converg 10, 24 (2023). DOI: 10.1186/s40580-023-00372-8 CrossRef Google Scholar
[48]	Liu MK, Choi DY. Extreme Huygens’ metasurfaces based on quasi-bound states in the continuum. Nano Lett 18, 8062–8069 (2018). DOI: 10.1021/acs.nanolett.8b04774 CrossRef Google Scholar
[49]	Kim G, Kim Y, Yun J et al. Metasurface-driven full-space structured light for three-dimensional imaging. Nat Commun 13, 5920 (2022). DOI: 10.1038/s41467-022-32117-2 CrossRef Google Scholar
[50]	Wang YJ, Chen QM, Yang WH et al. High-efficiency broadband achromatic metalens for near-IR biological imaging window. Nat Commun 12, 5560 (2021). DOI: 10.1038/s41467-021-25797-9 CrossRef Google Scholar
[51]	Chen WT, Zhu AY, Sisler J et al. A broadband achromatic polarization-insensitive metalens consisting of anisotropic nanostructures. Nat Commun 10, 355 (2019). DOI: 10.1038/s41467-019-08305-y CrossRef Google Scholar
[52]	Heiden JT, Jang MS. Design framework for polarization-insensitive multifunctional achromatic metalenses. Nanophotonics 11, 583–591 (2022). DOI: 10.1515/nanoph-2021-0638 CrossRef Google Scholar
[53]	Faraji-Dana M, Arbabi E, Arbabi A et al. Compact folded metasurface spectrometer. Nat Commun 9, 4196 (2018). DOI: 10.1038/s41467-018-06495-5 CrossRef Google Scholar
[54]	Cai GY, Li YH, Zhang Y et al. Compact angle-resolved metasurface spectrometer. Nat Mater 23, 71–78 (2024). DOI: 10.1038/s41563-023-01710-1 CrossRef Google Scholar
[55]	Wang RX, Ansari MA, Ahmed H et al. Compact multi-foci metalens spectrometer. Light Sci Appl 12, 103 (2023). DOI: 10.1038/s41377-023-01148-9 CrossRef Google Scholar
[56]	Faraji-Dana M, Arbabi E, Arbabi A et al. Folded planar metasurface spectrometer. In Proceedings of 2018 Conference on Lasers and Electro-Optics (CLEO) 1–2 (IEEE, 2018). Google Scholar
[57]	Liu WQ, Deng L, Li SF et al. High transmittance and broadband group delay metasurface element in Ka band. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT) 669–671 (IEEE, 2021); http://doi.org/10.1109/ICEICT53123.2021.9531170. Google Scholar
[58]	Miyamaru F, Morita H, Nishiyama Y et al. Ultrafast optical control of group delay of narrow-band terahertz waves. Sci Rep 4, 4346 (2014). DOI: 10.1038/srep04346 CrossRef Google Scholar
[59]	Jiang L, Li XZ, Wu QX et al. Neural network enabled metasurface design for phase manipulation. Opt Express 29, 2521–2528 (2021). DOI: 10.1364/OE.413079 CrossRef Google Scholar
[60]	Chen MZ, Cheng Q, Xia F et al. Metasurface‐based spatial phasers for analogue signal processing. Adv Opt Mater 8, 2000128 (2020). DOI: 10.1002/adom.202000128 CrossRef Google Scholar
[61]	Tsilipakos O, Koschny T, Soukoulis CM. Antimatched electromagnetic metasurfaces for broadband arbitrary phase manipulation in reflection. ACS Photonics 5, 1101–1107 (2018). DOI: 10.1021/acsphotonics.7b01415 CrossRef Google Scholar
[62]	Trubetskov MK, Von Pechmann M, Angelov IB et al. Measurements of the group delay and the group delay dispersion with resonance scanning interferometer. Opt Express 21, 6658–6669 (2013). DOI: 10.1364/OE.21.006658 CrossRef Google Scholar
[63]	Song NT, Xu NX, Shan DZ et al. Broadband achromatic metasurfaces for longwave infrared applications. Nanomaterials 11, 2760 (2021). DOI: 10.3390/nano11102760 CrossRef Google Scholar
[64]	He YL, Song BX, Tang J. Optical metalenses: fundamentals, dispersion manipulation, and applications. Front Optoelectron 15, 24 (2022). DOI: 10.1007/s12200-022-00017-4 CrossRef Google Scholar
[65]	Pan Y, Neuss S, Leifert A et al. Size‐dependent cytotoxicity of gold nanoparticles. Small 3, 1941–1949 (2007). DOI: 10.1002/smll.200700378 CrossRef Google Scholar
[66]	Gonçalves MR, Minassian H, Melikyan A. Plasmonic resonators: fundamental properties and applications. J Phys D Appl Phys 53, 443002 (2020). DOI: 10.1088/1361-6463/ab96e9 CrossRef Google Scholar
[67]	Xu Q, Zhang XQ, Xu YH et al. Plasmonic metalens based on coupled resonators for focusing of surface plasmons. Sci Rep 6, 37861 (2016). DOI: 10.1038/srep37861 CrossRef Google Scholar
[68]	Autore M, Hillenbrand R. What momentum mismatch. Nat Nanotechnol 14, 308–309 (2019). DOI: 10.1038/s41565-019-0390-5 CrossRef Google Scholar
[69]	Kim K, Oh Y, Ma K et al. Plasmon-enhanced total-internal-reflection fluorescence by momentum-mismatched surface nanostructures. Opt Lett 34, 3905–3907 (2009). DOI: 10.1364/OL.34.003905 CrossRef Google Scholar
[70]	Qin LS, Chen X, Zhang LL et al. Design, fabrication and testing of gain SPR sensor chip. J Phys Conf Ser 1209, 012006 (2019). DOI: 10.1088/1742-6596/1209/1/012006 CrossRef Google Scholar
[71]	Petryayeva E, Krull UJ. Localized surface plasmon resonance: nanostructures, bioassays and biosensing—A review. Anal Chim Acta 706, 8–24 (2011). DOI: 10.1016/j.aca.2011.08.020 CrossRef Google Scholar
[72]	Palermo G, Lininger A, Guglielmelli A et al. All-optical tunability of metalenses permeated with liquid crystals. ACS nano 16, 16539–16548 (2022). DOI: 10.1021/acsnano.2c05887 CrossRef Google Scholar
[73]	Park S, Hahn JW, Lee JY. Doubly resonant metallic nanostructure for high conversion efficiency of second harmonic generation. Opt Express 20, 4856–4870 (2012). DOI: 10.1364/OE.20.004856 CrossRef Google Scholar
[74]	Damgaard-Carstensen C, Ding F, Meng C et al. Demonstration of> 2π reflection phase range in optical metasurfaces based on detuned gap-surface plasmon resonators. Sci Rep 10, 19031 (2020). DOI: 10.1038/s41598-020-75931-8 CrossRef Google Scholar
[75]	Yao K, Liu YM. Plasmonic metamaterials. Nanotechnol Rev 3, 177–210 (2014). Google Scholar
[76]	Tong XC. Plasmonic metamaterials and metasurfaces. In Tong XC. Functional Metamaterials and Metadevices 129–153 (Springer, Cham, 2018). Google Scholar
[77]	Christopher P, Xin HL, Linic S. Visible-light-enhanced catalytic oxidation reactions on plasmonic silver nanostructures. Nat Chem 3, 467–472 (2011). DOI: 10.1038/nchem.1032 CrossRef Google Scholar
[78]	Barnard ES, White JS, Chandran A et al. Spectral properties of plasmonic resonator antennas. Opt Express 16, 16529–16537 (2008). DOI: 10.1364/OE.16.016529 CrossRef Google Scholar
[79]	Sun SL, He Q, Hao JM et al. Electromagnetic metasurfaces: physics and applications. Adv Opt Photonics 11, 380–479 (2019). DOI: 10.1364/AOP.11.000380 CrossRef Google Scholar
[80]	Pors A, Albrektsen O, Radko IP et al. Gap plasmon-based metasurfaces for total control of reflected light. Sci Rep 3, 2155 (2013). DOI: 10.1038/srep02155 CrossRef Google Scholar
[81]	Ding F, Yang YQ, Deshpande RA et al. A review of gap-surface plasmon metasurfaces: fundamentals and applications. Nanophotonics 7, 1129–1156 (2018). DOI: 10.1515/nanoph-2017-0125 CrossRef Google Scholar
[82]	Pors A, Bozhevolnyi SI. Plasmonic metasurfaces for efficient phase control in reflection. Opt Express 21, 27438–27451 (2013). DOI: 10.1364/OE.21.027438 CrossRef Google Scholar
[83]	Pors A, Nielsen MG, Eriksen RL et al. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces. Nano Lett 13, 829–834 (2013). DOI: 10.1021/nl304761m CrossRef Google Scholar
[84]	Boroviks S, Deshpande RA, Mortensen NA et al. Multifunctional metamirror: polarization splitting and focusing. ACS Photonics 5, 1648–1653 (2018). DOI: 10.1021/acsphotonics.7b01091 CrossRef Google Scholar
[85]	Cortés E, Wendisch FJ, Sortino L et al. Optical metasurfaces for energy conversion. Chem Rev 122, 15082–15176 (2022). DOI: 10.1021/acs.chemrev.2c00078 CrossRef Google Scholar
[86]	Linic S, Christopher P, Ingram DB. Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat Mater 10, 911–921 (2011). DOI: 10.1038/nmat3151 CrossRef Google Scholar
[87]	Gutruf P, Zou CJ, Withayachumnankul W et al. Mechanically tunable dielectric resonator metasurfaces at visible frequencies. Acs Nano 10, 133–141 (2016). DOI: 10.1021/acsnano.5b05954 CrossRef Google Scholar
[88]	Campione S, Basilio LI, Warne LK et al. Tailoring dielectric resonator geometries for directional scattering and Huygens’ metasurfaces. Opt Express 23, 2293–2307 (2015). DOI: 10.1364/OE.23.002293 CrossRef Google Scholar
[89]	Decker M, Staude I, Falkner M et al. High‐efficiency dielectric Huygens’ surfaces. Adv Opt Mater 3, 813–820 (2015). DOI: 10.1002/adom.201400584 CrossRef Google Scholar
[90]	Maier SA. Plasmonics: Fundamentals and Applications (Springer, New York, 2007). Google Scholar
[91]	Koshelev K, Kivshar Y. Dielectric resonant metaphotonics. ACS Photonics 8, 102–112 (2021). Google Scholar
[92]	Lin DM, Fan PY, Hasman E et al. Dielectric gradient metasurface optical elements. Science 345, 298–302 (2014). DOI: 10.1126/science.1253213 CrossRef Google Scholar
[93]	Devlin RC, Khorasaninejad M, Chen WT et al. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc Natl Acad Sci USA 113, 10473–10478 (2016). DOI: 10.1073/pnas.1611740113 CrossRef Google Scholar
[94]	Zhou SH, Shen ZX, Li XA et al. Liquid crystal integrated metalens with dynamic focusing property. Opt Lett 45, 4324–4327 (2020). DOI: 10.1364/OL.398601 CrossRef Google Scholar
[95]	Pan MY, Fu YF, Zheng MJ et al. Dielectric metalens for miniaturized imaging systems: progress and challenges. Light Sci Appl 11, 195 (2022). DOI: 10.1038/s41377-022-00885-7 CrossRef Google Scholar
[96]	Kerker M, Wang DS, Giles CL. Electromagnetic scattering by magnetic spheres. J Opt Soc Am 73, 765–767 (1983). DOI: 10.1364/JOSA.73.000765 CrossRef Google Scholar
[97]	Bukharin MM, Pecherkin VY, Ospanova AK et al. Transverse Kerker effect in all-dielectric spheroidal particles. Sci Rep 12, 7997 (2022). DOI: 10.1038/s41598-022-11733-4 CrossRef Google Scholar
[98]	Liu W, Kivshar YS. Generalized Kerker effects in nanophotonics and meta-optics [Invited]. Opt Express 26, 13085–13105 (2018). DOI: 10.1364/OE.26.013085 CrossRef Google Scholar
[99]	Liu WW, Li ZC, Cheng H et al. Dielectric resonance-based optical metasurfaces: from fundamentals to applications. iScience 23, 101868 (2020). DOI: 10.1016/j.isci.2020.101868 CrossRef Google Scholar
[100]	Genevet P, Capasso F, Aieta F et al. Recent advances in planar optics: from plasmonic to dielectric metasurfaces. Optica 4, 139–152 (2017). DOI: 10.1364/OPTICA.4.000139 CrossRef Google Scholar
[101]	Long S, McAllister M, Shen L. The resonant cylindrical dielectric cavity antenna. IEEE Trans Antennas Propag 31, 406–412 (1983). DOI: 10.1109/TAP.1983.1143080 CrossRef Google Scholar
[102]	Wang SW, Lai JJ, Wu T et al. Wide-band achromatic metalens for visible light by dispersion compensation method. J Phys D Appl Phys 50, 455101 (2017). DOI: 10.1088/1361-6463/aa8c90 CrossRef Google Scholar
[103]	Rytov S. Electromagnetic properties of a finely stratified medium. Sov Phys JEPT 2, 466–475 (1956). Google Scholar
[104]	Vo S, Fattal D, Sorin WV et al. Sub-wavelength grating lenses with a twist. IEEE Photonics Technol Lett 26, 1375–1378 (2014). DOI: 10.1109/LPT.2014.2325947 CrossRef Google Scholar
[105]	Arbabi A, Horie Y, Ball AJ et al. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat Commun 6, 7069 (2015). DOI: 10.1038/ncomms8069 CrossRef Google Scholar
[106]	Powell DA. Interference between the modes of an all-dielectric meta-atom. Phys Rev Appl 7, 034006 (2017). DOI: 10.1103/PhysRevApplied.7.034006 CrossRef Google Scholar
[107]	Wang Q, Rogers ETF, Gholipour B et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat Photonics 10, 60–65 (2016). DOI: 10.1038/nphoton.2015.247 CrossRef Google Scholar
[108]	Zhang YF, Fowler C, Liang JH et al. Electrically reconfigurable non-volatile metasurface using low-loss optical phase-change material. Nat Nanotechnol 16, 661–666 (2021). DOI: 10.1038/s41565-021-00881-9 CrossRef Google Scholar
[109]	Abdollahramezani S, Hemmatyar O, Taghinejad M et al. Electrically driven reprogrammable phase-change metasurface reaching 80% efficiency. Nat Commun 13, 1696 (2022). DOI: 10.1038/s41467-022-29374-6 CrossRef Google Scholar
[110]	Wang Y, Cui DJ, Wang Y et al. Electrically and thermally tunable multifunctional terahertz metasurface array. Phys Rev A 105, 033520 (2022). DOI: 10.1103/PhysRevA.105.033520 CrossRef Google Scholar
[111]	Shao ZW, Cao X, Luo HJ et al. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mater 10, 581–605 (2018). DOI: 10.1038/s41427-018-0061-2 CrossRef Google Scholar
[112]	Shalaginov MY, An SS, Zhang YF et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat Commun 12, 1225 (2021). DOI: 10.1038/s41467-021-21440-9 CrossRef Google Scholar
[113]	Zhang WH, Wu XQ, Li L et al. Fabrication of a VO₂-based tunable metasurface by electric-field scanning probe lithography with precise depth control. ACS Appl Mater Interfaces 15, 13517–13525 (2023). DOI: 10.1021/acsami.2c21935 CrossRef Google Scholar
[114]	Hashemi MRM, Yang SH, Wang TY et al. Electronically-controlled beam-steering through vanadium dioxide metasurfaces. Sci Rep 6, 35439 (2016). DOI: 10.1038/srep35439 CrossRef Google Scholar
[115]	King J, Wan CH, Park TJ et al. Electrically tunable VO₂–metal metasurface for mid-infrared switching, limiting and nonlinear isolation. Nat Photonics 18, 74–80 (2024). DOI: 10.1038/s41566-023-01324-8 CrossRef Google Scholar
[116]	Wan CH, Zhang Z, Woolf D et al. On the optical properties of thin‐film vanadium dioxide from the visible to the far infrared. Ann Phys 531, 1900188 (2019). DOI: 10.1002/andp.201900188 CrossRef Google Scholar
[117]	Chu F, Tian LL, Li R et al. Adaptive nematic liquid crystal lens array with resistive layer. Liq Cryst 47, 563–571 (2020). DOI: 10.1080/02678292.2019.1662502 CrossRef Google Scholar
[118]	Kang DH, Heo HS, Yang YH et al. Liquid crystal-integrated metasurfaces for an active photonic platform. Opto-Electron Adv 7, 230216 (2024). DOI: 10.29026/oea.2024.230216 CrossRef Google Scholar
[119]	Chang X, Pivnenko M, Shrestha P et al. Electrically tuned active metasurface towards metasurface-integrated liquid crystal on silicon (meta-LCoS) devices. Opt Express 31, 5378–5387 (2023). DOI: 10.1364/OE.483452 CrossRef Google Scholar
[120]	Ji YY, Fan F, Zhang X et al. Active terahertz anisotropy and dispersion engineering based on dual-frequency liquid crystal and dielectric metasurface. J Lightwave Technol 38, 4030–4036 (2020). Google Scholar
[121]	Rocco D, Carletti L, Caputo R et al. Switching the second harmonic generation by a dielectric metasurface via tunable liquid crystal. Opt Express 28, 12037–12046 (2020). DOI: 10.1364/OE.386776 CrossRef Google Scholar
[122]	Badloe T, Kim Y, Kim J et al. Bright-field and edge-enhanced imaging using an electrically tunable dual-mode metalens. ACS Nano 17, 14678–14685 (2023). DOI: 10.1021/acsnano.3c02471 CrossRef Google Scholar
[123]	Bosch M, Shcherbakov MR, Won K et al. Electrically actuated varifocal lens based on liquid-crystal-embedded dielectric metasurfaces. Nano Lett 21, 3849–3856 (2021). DOI: 10.1021/acs.nanolett.1c00356 CrossRef Google Scholar
[124]	Kamali SM, Arbabi A, Arbabi E et al. Decoupling optical function and geometrical form using conformal flexible dielectric metasurfaces. Nat Commun 7, 11618 (2016). DOI: 10.1038/ncomms11618 CrossRef Google Scholar
[125]	Kamali SM, Arbabi E, Arbabi A et al. Highly tunable elastic dielectric metasurface lenses. Laser Photonics Rev 10, 1002–1008 (2016). DOI: 10.1002/lpor.201600144 CrossRef Google Scholar
[126]	Li J, Fan HJ, Ye H et al. Design of multifunctional tunable metasurface assisted by elastic substrate. Nanomaterials 12, 2387 (2022). DOI: 10.3390/nano12142387 CrossRef Google Scholar
[127]	Li WL, He P, Lei DY et al. Super-resolution multicolor fluorescence microscopy enabled by an apochromatic super-oscillatory lens with extended depth-of-focus. Nat Commun 14, 5107 (2023). DOI: 10.1038/s41467-023-40725-9 CrossRef Google Scholar
[128]	Ren YX, He HS, Tang HJ et al. Non-diffracting light wave: fundamentals and biomedical applications. Front Phys 9, 698343 (2021). DOI: 10.3389/fphy.2021.698343 CrossRef Google Scholar
[129]	Bouchal Z. Nondiffracting optical beams: physical properties, experiments, and applications. Czech J Phys 53, 537–578 (2003). DOI: 10.1023/A:1024802801048 CrossRef Google Scholar
[130]	Li DC, Wang XR, Ling JZ et al. Planar efficient metasurface for generation of Bessel beam and super-resolution focusing. Opt Quant Electron 53, 143 (2021). DOI: 10.1007/s11082-021-02765-7 CrossRef Google Scholar
[131]	Lin ZM, Li XW, Zhao RZ et al. High-efficiency Bessel beam array generation by Huygens metasurfaces. Nanophotonics 8, 1079–1085 (2019). DOI: 10.1515/nanoph-2019-0085 CrossRef Google Scholar
[132]	Shi FH, Qiu M, Zhang L et al. Multiplane illumination enabled by Fourier-transform metasurfaces for high-speed light-sheet microscopy. ACS Photonics 5, 1676–1684 (2018). DOI: 10.1021/acsphotonics.7b01457 CrossRef Google Scholar
[133]	Li CS, Guo YH, Chang XZ et al. A metasurface-on-fiber light-sheet generator for biological imaging. Opt Commun 559, 130378 (2024). DOI: 10.1016/j.optcom.2024.130378 CrossRef Google Scholar
[134]	Luo Y, Tseng ML, Vyas S et al. Metasurface‐based abrupt autofocusing beam for biomedical applications. Small Methods 6, 2101228 (2022). DOI: 10.1002/smtd.202101228 CrossRef Google Scholar
[135]	Lu RW, Liang YJ, Meng GH et al. Rapid mesoscale volumetric imaging of neural activity with synaptic resolution. Nat Methods 17, 291–294 (2020). DOI: 10.1038/s41592-020-0760-9 CrossRef Google Scholar
[136]	Wang XW, Nie ZQ, Liang Y et al. Recent advances on optical vortex generation. Nanophotonics 7, 1533–1556 (2018). DOI: 10.1515/nanoph-2018-0072 CrossRef Google Scholar
[137]	Wang S, Li L, Wen S et al. Metalens for accelerated optoelectronic edge detection under ambient illumination. Nano Lett 24, 356–361 (2023). Google Scholar
[138]	Zheludev NI. What diffraction limit. Nat Mater 7, 420–422 (2008). DOI: 10.1038/nmat2163 CrossRef Google Scholar
[139]	Hänninen P. Beyond the diffraction limit. Nature 419, 802 (2002). Google Scholar
[140]	Park SC, Park MK, Kang MG. Super-resolution image reconstruction: a technical overview. IEEE Signal Process Mag 20, 21–36 (2003). DOI: 10.1109/MSP.2003.1203207 CrossRef Google Scholar
[141]	Huang B, Babcock H, Zhuang XW. Breaking the diffraction barrier: super-resolution imaging of cells. Cell 143, 1047–1058 (2010). DOI: 10.1016/j.cell.2010.12.002 CrossRef Google Scholar
[142]	Bliokh KY, Bekshaev AY, Nori F. Extraordinary momentum and spin in evanescent waves. Nat Commun 5, 3300 (2014). DOI: 10.1038/ncomms4300 CrossRef Google Scholar
[143]	Loerke D, Preitz B, Stuhmer W et al. Super-resolution measurements with evanescent-wave fluorescence-excitation using variable beam incidence. J Biomed Opt 5, 23–30 (2000). DOI: 10.1117/1.429964 CrossRef Google Scholar
[144]	Pendry JB. Negative refraction makes a perfect lens. Phys Rev Lett 85, 3966–3969 (2000). DOI: 10.1103/PhysRevLett.85.3966 CrossRef Google Scholar
[145]	Fang N, Lee H, Sun C et al. Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005). DOI: 10.1126/science.1108759 CrossRef Google Scholar
[146]	Lu D, Liu ZW. Hyperlenses and metalenses for far-field super-resolution imaging. Nat Commun 3, 1205 (2012). DOI: 10.1038/ncomms2176 CrossRef Google Scholar
[147]	Kim M, So S, Yao K et al. Deep sub-wavelength nanofocusing of UV-visible light by hyperbolic metamaterials. Sci Rep 6, 38645 (2016). DOI: 10.1038/srep38645 CrossRef Google Scholar
[148]	Jacob Z, Alekseyev LV, Narimanov E. Optical hyperlens: far-field imaging beyond the diffraction limit. Opt Express 14, 8247–8256 (2006). DOI: 10.1364/OE.14.008247 CrossRef Google Scholar
[149]	Liu ZW, Lee H, Xiong Y et al. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007). DOI: 10.1126/science.1137368 CrossRef Google Scholar
[150]	Kastrup L, Blom H, Eggeling C et al. Fluorescence fluctuation spectroscopy in subdiffraction focal volumes. Phys Rev Lett 94, 178104 (2005). DOI: 10.1103/PhysRevLett.94.178104 CrossRef Google Scholar
[151]	Honigmann A, Mueller V, Ta H et al. Scanning STED-FCS reveals spatiotemporal heterogeneity of lipid interaction in the plasma membrane of living cells. Nat Commun 5, 5412 (2014). DOI: 10.1038/ncomms6412 CrossRef Google Scholar
[152]	Barulin A, Kim I. Hyperlens for capturing sub-diffraction nanoscale single molecule dynamics. Opt Express 31, 12162–12174 (2023). DOI: 10.1364/OE.486702 CrossRef Google Scholar
[153]	Wei FF, Ponsetto JL, Liu ZW. Plasmonic structured illumination microscopy. In Liu ZW. Plasmonics and Super-Resolution Imaging 127–163 (Jenny Stanford Publishing, New York, 2017). Google Scholar
[154]	Wei FF, Lu D, Shen H et al. Wide field super-resolution surface imaging through plasmonic structured illumination microscopy. Nano Lett 14, 4634–4639 (2014). DOI: 10.1021/nl501695c CrossRef Google Scholar
[155]	Wei SB, Lei T, Du LP et al. Sub-100nm resolution PSIM by utilizing modified optical vortices with fractional topological charges for precise phase shifting. Opt Express 23, 30143–30148 (2015). DOI: 10.1364/OE.23.030143 CrossRef Google Scholar
[156]	Ponsetto JL, Wei FF, Liu ZW. Localized plasmon assisted structured illumination microscopy for wide-field high-speed dispersion-independent super resolution imaging. Nanoscale 6, 5807–5812 (2014). DOI: 10.1039/C4NR00443D CrossRef Google Scholar
[157]	Ponsetto JL, Bezryadina A, Wei FF et al. Experimental demonstration of localized plasmonic structured illumination microscopy. ACS Nano 11, 5344–5350 (2017). DOI: 10.1021/acsnano.7b01158 CrossRef Google Scholar
[158]	Lee YU, Li SL, Wisna GBM et al. Hyperbolic material enhanced scattering nanoscopy for label-free super-resolution imaging. Nat Commun 13, 6631 (2022). DOI: 10.1038/s41467-022-34553-6 CrossRef Google Scholar
[159]	Rogers ETF, Lindberg J, Roy T et al. A super-oscillatory lens optical microscope for subwavelength imaging. Nat Mater 11, 432–435 (2012). DOI: 10.1038/nmat3280 CrossRef Google Scholar
[160]	Berry MV, Popescu S. Evolution of quantum superoscillations and optical superresolution without evanescent waves. J Phys A: Math Gen 39, 6965–6977 (2006). DOI: 10.1088/0305-4470/39/22/011 CrossRef Google Scholar
[161]	Aharonov Y, Albert DZ, Vaidman L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys Rev Lett 60, 1351–1354 (1988). DOI: 10.1103/PhysRevLett.60.1351 CrossRef Google Scholar
[162]	Huang FM, Zheludev N, Chen YF et al. Focusing of light by a nanohole array. Appl Phys Lett 90, 091119 (2007). DOI: 10.1063/1.2710775 CrossRef Google Scholar
[163]	Zheludev NI, Yuan G. Optical superoscillation technologies beyond the diffraction limit. Nat Rev Phys 4, 16–32 (2022). Google Scholar
[164]	Chen G, Wen ZQ, Qiu CW. Superoscillation: from physics to optical applications. Light Sci Appl 8, 56 (2019). DOI: 10.1038/s41377-019-0163-9 CrossRef Google Scholar
[165]	Qin F, Huang K, Wu JF et al. A supercritical lens optical label‐free microscopy: sub‐diffraction resolution and ultra‐long working distance. Adv Mater 29, 1602721 (2017). DOI: 10.1002/adma.201602721 CrossRef Google Scholar
[166]	Li Z, Zhang T, Wang YQ et al. Achromatic Broadband super‐resolution imaging by super‐oscillatory metasurface. Laser Photonics Rev 12, 1800064 (2018). DOI: 10.1002/lpor.201800064 CrossRef Google Scholar
[167]	Yuan GH, Rogers ETF, Zheludev NI. Achromatic super-oscillatory lenses with sub-wavelength focusing. Light Sci Appl 6, e17036 (2017). DOI: 10.1038/lsa.2017.36 CrossRef Google Scholar
[168]	Rogers ETF, Savo S, Lindberg J et al. Super-oscillatory optical needle. Appl Phys Lett 102, 031108 (2013). DOI: 10.1063/1.4774385 CrossRef Google Scholar
[169]	Roy T, Rogers ETF, Yuan GH et al. Point spread function of the optical needle super-oscillatory lens. Appl Phys Lett 104, 231109 (2014). DOI: 10.1063/1.4882246 CrossRef Google Scholar
[170]	Yuan GH, Rogers ETF, Roy T et al. Planar super-oscillatory lens for sub-diffraction optical needles at violet wavelengths. Sci Rep 4, 6333 (2014). DOI: 10.1038/srep06333 CrossRef Google Scholar
[171]	Diao JS, Yuan WZ, Yu YT et al. Controllable design of super-oscillatory planar lenses for sub-diffraction-limit optical needles. Opt Express 24, 1924–1933 (2016). DOI: 10.1364/OE.24.001924 CrossRef Google Scholar
[172]	Chen G, Wu ZX, Yu AP et al. Planar binary-phase lens for super-oscillatory optical hollow needles. Sci Rep 7, 4697 (2017). DOI: 10.1038/s41598-017-05060-2 CrossRef Google Scholar
[173]	Solli DR, Jalali B. Analog optical computing. Nat Photonics 9, 704–706 (2015). DOI: 10.1038/nphoton.2015.208 CrossRef Google Scholar
[174]	He SS, Wang RS, Luo HL. Computing metasurfaces for all-optical image processing: a brief review. Nanophotonics 11, 1083–1108 (2022). DOI: 10.1515/nanoph-2021-0823 CrossRef Google Scholar
[175]	Selinummi J, Ruusuvuori P, Podolsky I et al. Bright field microscopy as an alternative to whole cell fluorescence in automated analysis of macrophage images. PLoS One 4, e7497 (2009). DOI: 10.1371/journal.pone.0007497 CrossRef Google Scholar
[176]	Marr D, Hildreth E. Theory of edge detection. Proc Roy Soc B Biol Sci 207, 187–217 (1980). Google Scholar
[177]	Canny J. A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell PAMI-8, 679–698 (1986). DOI: 10.1109/TPAMI.1986.4767851 CrossRef Google Scholar
[178]	Maini R, Aggarwal H. Study and comparison of various image edge detection techniques. Int J Image Process 3, 1–12 (2009). DOI: 10.1049/iet-ipr:20080080 CrossRef Google Scholar
[179]	Wang JK, Zhang WH, Qi QQ et al. Gradual edge enhancement in spiral phase contrast imaging with fractional vortex filters. Sci Rep 5, 15826 (2015). DOI: 10.1038/srep15826 CrossRef Google Scholar
[180]	Wei SB, Zhu SW, Yuan XC. Image edge enhancement in optical microscopy with a Bessel-like amplitude modulated spiral phase filter. J Opt 13, 105704 (2011). DOI: 10.1088/2040-8978/13/10/105704 CrossRef Google Scholar
[181]	Yuan S, Xiang D, Liu XM et al. Edge detection based on computational ghost imaging with structured illuminations. Opt Commun 410, 350–355 (2018). DOI: 10.1016/j.optcom.2017.10.016 CrossRef Google Scholar
[182]	Zhou Y, Zheng HY, Kravchenko II et al. Flat optics for image differentiation. Nat Photonics 14, 316–323 (2020). DOI: 10.1038/s41566-020-0591-3 CrossRef Google Scholar
[183]	Chen MK, Wu YF, Feng L et al. Principles, functions, and applications of optical meta‐lens. Adv Opt Mater 9, 2001414 (2021). DOI: 10.1002/adom.202001414 CrossRef Google Scholar
[184]	Abdollahramezani S, Hemmatyar O, Adibi A. Meta-optics for spatial optical analog computing. Nanophotonics 9, 4075–4095 (2020). DOI: 10.1515/nanoph-2020-0285 CrossRef Google Scholar
[185]	Wan L, Pan DP, Yang SF et al. Optical analog computing of spatial differentiation and edge detection with dielectric metasurfaces. Opt Lett 45, 2070–2073 (2020). DOI: 10.1364/OL.386986 CrossRef Google Scholar
[186]	Zhou JX, Qian HL, Zhao JX et al. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl Sci Rev 8, nwaa176 (2021). DOI: 10.1093/nsr/nwaa176 CrossRef Google Scholar
[187]	Guo C, Xiao M, Minkov M et al. Photonic crystal slab Laplace operator for image differentiation. Optica 5, 251–256 (2018). DOI: 10.1364/OPTICA.5.000251 CrossRef Google Scholar
[188]	Kim Y, Lee GY, Sung J et al. Spiral metalens for phase contrast imaging. Adv Funct Mater 32, 2106050 (2022). DOI: 10.1002/adfm.202106050 CrossRef Google Scholar
[189]	Dong HG, Wang FQ, Liang RS et al. Visible-wavelength metalenses for diffraction-limited focusing of double polarization and vortex beams. Opt Mater Express 7, 4029–4037 (2017). DOI: 10.1364/OME.7.004029 CrossRef Google Scholar
[190]	Zhou C, Chen YJ, Li Y et al. Laplace differentiator based on metasurface with toroidal dipole resonance. Adv Funct Mater 34, 2313777 (2024). DOI: 10.1002/adfm.202313777 CrossRef Google Scholar
[191]	Chu CH, Chia YH, Hsu HC et al. Intelligent phase contrast meta-microscope system. Nano Lett 23, 11630–11637 (2023). DOI: 10.1021/acs.nanolett.3c03484 CrossRef Google Scholar
[192]	Overvig A, Alù A. Diffractive nonlocal metasurfaces. Laser Photonics Rev 16, 2100633 (2022). DOI: 10.1002/lpor.202100633 CrossRef Google Scholar
[193]	Shastri K, Monticone F. Nonlocal flat optics. Nat Photonics 17, 36–47 (2023). DOI: 10.1038/s41566-022-01098-5 CrossRef Google Scholar
[194]	Kim M, Lee D, Kim J et al. Nonlocal metasurfaces‐enabled analog light localization for imaging and lithography. Laser Photonics Rev 18, 2300718 (2024). DOI: 10.1002/lpor.202300718 CrossRef Google Scholar
[195]	Li, Shiyu, and Chia Wei Hsu. Thickness bound for nonlocal wide-field-of-view metalenses. Light: Science & Applications 11.1, 338 (2022). DOI: 10.1103/PhysRevLett.121.173004 CrossRef Google Scholar
[196]	Kwon H, Sounas D, Cordaro A et al. Nonlocal metasurfaces for optical signal processing. Phys Rev Lett 121 , 173004 (2018). Google Scholar
[197]	Kwon H, Cordaro A, Sounas D et al. Dual-polarization analog 2D image processing with nonlocal metasurfaces. ACS Photonics 7, 1799–1805 (2020). DOI: 10.1021/acsphotonics.0c00473 CrossRef Google Scholar
[198]	Arnison MR, Larkin KG, Sheppard CJR et al. Linear phase imaging using differential interference contrast microscopy. J Microsc 214, 7–12 (2004). DOI: 10.1111/j.0022-2720.2004.01293.x CrossRef Google Scholar
[199]	Zernike F. How I discovered phase contrast. Science 121, 345–349 (1955). DOI: 10.1126/science.121.3141.345 CrossRef Google Scholar
[200]	Preza C, Snyder DL, Conchello JA. Theoretical development and experimental evaluation of imaging models for differential-interference-contrast microscopy. J Opt Soc Am A 16, 2185–2199 (1999). DOI: 10.1364/JOSAA.16.002185 CrossRef Google Scholar
[201]	Preza C. Rotational-diversity phase estimation from differential-interference-contrast microscopy images. J Opt Soc Am A 17, 415–424 (2000). DOI: 10.1364/JOSAA.17.000415 CrossRef Google Scholar
[202]	Shribak M. Quantitative orientation-independent differential interference contrast microscope with fast switching shear direction and bias modulation. J Opt Soc Am A 30, 769–782 (2013). DOI: 10.1364/JOSAA.30.000769 CrossRef Google Scholar
[203]	Zhao Q, Kang L, Du B et al. Electrically tunable negative permeability metamaterials based on nematic liquid crystals. Appl Phys Lett 90, 011112 (2007). DOI: 10.1063/1.2430485 CrossRef Google Scholar
[204]	Kang B, Woo JH, Choi E et al. Optical switching of near infrared light transmission in metamaterial-liquid crystal cell structure. Opt Express 18, 16492–16498 (2010). DOI: 10.1364/OE.18.016492 CrossRef Google Scholar
[205]	Zhang FL, Zhang WH, Zhao Q et al. Electrically controllable fishnet metamaterial based on nematic liquid crystal. Opt Express 19, 1563–1568 (2011). DOI: 10.1364/OE.19.001563 CrossRef Google Scholar
[206]	Su H, Wang H, Zhao H et al. Liquid-crystal-based electrically tuned electromagnetically induced transparency metasurface switch. Sci Rep 7, 17378 (2017). DOI: 10.1038/s41598-017-17612-7 CrossRef Google Scholar
[207]	Yu P, Li JX, Liu N. Electrically tunable optical metasurfaces for dynamic polarization conversion. Nano Lett 21, 6690–6695 (2021). DOI: 10.1021/acs.nanolett.1c02318 CrossRef Google Scholar
[208]	Badloe T, Kim I, Kim Y et al. Electrically tunable bifocal metalens with diffraction‐limited focusing and imaging at visible wavelengths. Adv Sci 8, 2102646 (2021). DOI: 10.1002/advs.202102646 CrossRef Google Scholar
[209]	Zhou SL, Wu YF, Chen SR et al. Phase change induced active metasurface devices for dynamic wavefront control. J Phys D Appl Phys 53, 204001 (2020). DOI: 10.1088/1361-6463/ab7560 CrossRef Google Scholar
[210]	Ee HS, Agarwal R. Tunable metasurface and flat optical zoom lens on a stretchable substrate. Nano Lett 16, 2818–2823 (2016). DOI: 10.1021/acs.nanolett.6b00618 CrossRef Google Scholar
[211]	Tseng ML, Hsiao HH, Chu CH et al. Metalenses: advances and applications. Adv Opt Mater 6, 1800554 (2018). DOI: 10.1002/adom.201800554 CrossRef Google Scholar
[212]	Dirdal CA, Thrane PCV, Dullo FT et al. MEMS-tunable dielectric metasurface lens using thin-film PZT for large displacements at low voltages. Opt Lett 47, 1049–1052 (2022). DOI: 10.1364/OL.451750 CrossRef Google Scholar
[213]	Han ZY, Colburn S, Majumdar A et al. MEMS-actuated metasurface Alvarez lens. Microsystems 6, 79 (2020). Google Scholar
[214]	Arbabi E, Arbabi A, Kamali SM et al. MEMS-tunable dielectric metasurface lens. Nat Commun 9, 812 (2018). DOI: 10.1038/s41467-018-03155-6 CrossRef Google Scholar
[215]	Luo Y, Chu CH, Vyas S et al. Varifocal metalens for optical sectioning fluorescence microscopy. Nano Lett 21, 5133–5142 (2021). DOI: 10.1021/acs.nanolett.1c01114 CrossRef Google Scholar
[216]	Kim Y, Wu PC, Sokhoyan R et al. Phase modulation with electrically tunable vanadium dioxide phase-change metasurfaces. Nano Lett 19, 3961–3968 (2019). DOI: 10.1021/acs.nanolett.9b01246 CrossRef Google Scholar
[217]	Bai W, Yang P, Huang J et al. Near-infrared tunable metalens based on phase change material Ge₂Sb₂Te₅. Sci Rep 9, 5368 (2019). DOI: 10.1038/s41598-019-41859-x CrossRef Google Scholar
[218]	Afridi A, Gieseler J, Meyer N et al. Ultrathin tunable optomechanical metalens. Nano Lett 23, 2496–2501 (2023). DOI: 10.1021/acs.nanolett.2c04105 CrossRef Google Scholar
[219]	Song YK, Liu WC, Wang XL et al. Multifunctional metasurface lens with tunable focus based on phase transition material. Front Phys 9, 651898 (2021). DOI: 10.3389/fphy.2021.651898 CrossRef Google Scholar
[220]	Crosson B, Ford A, McGregor KM et al. Functional imaging and related techniques: an introduction for rehabilitation researchers. J Rehabil Res Dev 47, vii–xxxiv (2010). Google Scholar
[221]	Tsao J. Ultrafast imaging: principles, pitfalls, solutions, and applications. J Magn Reson Imaging 32, 252–266 (2010). DOI: 10.1002/jmri.22239 CrossRef Google Scholar
[222]	Sezgin E, Schneider F, Galiani S et al. Measuring nanoscale diffusion dynamics in cellular membranes with super-resolution STED–FCS. Nat Protoc 14, 1054–1083 (2019). Google Scholar
[223]	Schermelleh L, Ferrand A, Huser T et al. Super-resolution microscopy demystified. Nat Cell Biol 21, 72–84 (2019). DOI: 10.1038/s41556-018-0251-8 CrossRef Google Scholar
[224]	Kuhlmann AV, Houel J, Brunner D et al. A dark-field microscope for background-free detection of resonance fluorescence from single semiconductor quantum dots operating in a set-and-forget mode. Rev Sci Instrum 84, 073905 (2013). DOI: 10.1063/1.4813879 CrossRef Google Scholar
[225]	Beard P. Biomedical photoacoustic imaging. Interface Focus 1, 602–631 (2011). DOI: 10.1098/rsfs.2011.0028 CrossRef Google Scholar
[226]	Balasubramani V, Kuś A, Tu HY et al. Holographic tomography: techniques and biomedical applications [Invited]. Appl Opt 60, B65–B80 (2021). DOI: 10.1364/AO.416902 CrossRef Google Scholar
[227]	Wang H, Akkin T, Magnain C et al. Polarization sensitive optical coherence microscopy for brain imaging. Opt Lett 41, 2213–2216 (2016). DOI: 10.1364/OL.41.002213 CrossRef Google Scholar
[228]	Baumann B. Polarization sensitive optical coherence tomography: a review of technology and applications. Appl Sci 7, 474 (2017). DOI: 10.3390/app7050474 CrossRef Google Scholar
[229]	Girkin JM, Carvalho MT. The light-sheet microscopy revolution. J Opt 20, 053002 (2018). DOI: 10.1088/2040-8986/aab58a CrossRef Google Scholar
[230]	Chen BC, Legant WR, Wang K et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998 (2014). DOI: 10.1126/science.1257998 CrossRef Google Scholar
[231]	Stelzer EHK, Strobl F, Chang BJ et al. Light sheet fluorescence microscopy. Nat Rev Methods Primers 1, 73 (2021). DOI: 10.1038/s43586-021-00069-4 CrossRef Google Scholar
[232]	Archetti A, Bruzzone M, Tagliabue G et al. Generation of Bessel beam lattices by a single metasurface for neuronal activity recording in zebrafish larva. bioRxiv (2023). https://www.biorxiv.org/content/10.1101/2023.02.12.528189v1 Google Scholar
[233]	Arbabi E, Li JQ, Hutchins RJ et al. Two-photon microscopy with a double-wavelength metasurface objective lens. Nano Lett 18, 4943–4948 (2018). DOI: 10.1021/acs.nanolett.8b01737 CrossRef Google Scholar
[234]	Rynes ML, Surinach DA, Linn S et al. Miniaturized head-mounted microscope for whole-cortex mesoscale imaging in freely behaving mice. Nat Methods 18, 417–425 (2021). DOI: 10.1038/s41592-021-01104-8 CrossRef Google Scholar
[235]	Yao J, Lin R, Chen MK et al. Integrated-resonant metadevices: a review. Adv Photonics 5, 024001 (2023). Google Scholar
[236]	Colburn S, Zhan AL, Majumdar A. Metasurface optics for full-color computational imaging. Sci Adv 4, eaar2114 (2018). DOI: 10.1126/sciadv.aar2114 CrossRef Google Scholar
[237]	Avayu O, Almeida E, Prior Y et al. Composite functional metasurfaces for multispectral achromatic optics. Nat Commun 8, 14992 (2017). DOI: 10.1038/ncomms14992 CrossRef Google Scholar
[238]	Hua X, Wang YJ, Wang SM et al. Ultra-compact snapshot spectral light-field imaging. Nat Commun 13, 2732 (2022). DOI: 10.1038/s41467-022-30439-9 CrossRef Google Scholar
[239]	Tseng E, Colburn S, Whitehead J et al. Neural nano-optics for high-quality thin lens imaging. Nat Commun 12, 6493 (2021). DOI: 10.1038/s41467-021-26443-0 CrossRef Google Scholar
[240]	Chakravarthula P, Sun JP, Li X et al. Thin on-sensor nanophotonic array cameras. ACM Trans Graph 42, 249 (2023). Google Scholar
[241]	Park B, Oh D, Kim J et al. Functional photoacoustic imaging: from nano- and micro- to macro-scale. Nano Converg 10, 29 (2023). DOI: 10.1186/s40580-023-00377-3 CrossRef Google Scholar
[242]	Park B, Lee KM, Park S et al. Deep tissue photoacoustic imaging of nickel(II) dithiolene-containing polymeric nanoparticles in the second near-infrared window. Theranostics 10, 2509–2521 (2020). DOI: 10.7150/thno.39403 CrossRef Google Scholar
[243]	Wang DP, Wang YH, Wang WR et al. Deep tissue photoacoustic computed tomography with a fast and compact laser system. Biomed Opt Express 8, 112–123 (2017). DOI: 10.1364/BOE.8.000112 CrossRef Google Scholar
[244]	Zhao YT, Guo CK, Zhang YQ et al. Ultraviolet metalens for photoacoustic microscopy with an elongated depth of focus. Opt Lett 48, 3435–3438 (2023). DOI: 10.1364/OL.485946 CrossRef Google Scholar
[245]	Li DW, Humayun L, Vienneau E et al. Seeing through the skin: photoacoustic tomography of skin vasculature and beyond. JID innov 1, 100039 (2021). DOI: 10.1016/j.xjidi.2021.100039 CrossRef Google Scholar
[246]	Yao JJ, Wang LV. Sensitivity of photoacoustic microscopy. Photoacoustics 2, 87–101 (2014). DOI: 10.1016/j.pacs.2014.04.002 CrossRef Google Scholar
[247]	Liu WW, Li PC. Photoacoustic imaging of cells in a three-dimensional microenvironment. J Biomed Sci 27, 3 (2020). DOI: 10.1186/s12929-019-0594-x CrossRef Google Scholar
[248]	Liang YZ, Fu WB, Li Q et al. Optical-resolution functional gastrointestinal photoacoustic endoscopy based on optical heterodyne detection of ultrasound. Nat Commun 13, 7604 (2022). DOI: 10.1038/s41467-022-35259-5 CrossRef Google Scholar
[249]	Tearney GJ, Boppart SA, Bouma BE et al. Scanning single-mode fiber optic catheter–endoscope for optical coherence tomography: erratum. Opt Lett 21, 912 (1996). DOI: 10.1364/OL.21.000912 CrossRef Google Scholar
[250]	Tearney GJ, Brezinski ME, Bouma BE et al. In vivo endoscopic optical biopsy with optical coherence tomography. Science 276, 2037–2039 (1997). DOI: 10.1126/science.276.5321.2037 CrossRef Google Scholar
[251]	Hariri LP, Adams DC, Wain JC et al. Endobronchial optical coherence tomography for low-risk microscopic assessment and diagnosis of idiopathic pulmonary fibrosis in vivo. Am J Respir Crit Care Med 197, 949–952 (2018). DOI: 10.1164/rccm.201707-1446LE CrossRef Google Scholar
[252]	Yang JY, Ghimire I, Wu PC et al. Photonic crystal fiber metalens. Nanophotonics 8, 443–449 (2019). DOI: 10.1515/nanoph-2018-0204 CrossRef Google Scholar
[253]	Drexler W. Ultrahigh-resolution optical coherence tomography. J Biomed Opt 9, 47–74 (2004). DOI: 10.1117/1.1629679 CrossRef Google Scholar
[254]	Aumann S, Donner S, Fischer J et al. Optical coherence tomography (OCT): principle and technical realization. In Bille JF. High Resolution Imaging in Microscopy and Ophthalmology: New Frontiers in Biomedical Optics 59–85 (Springer, Cham, 2019). Google Scholar
[255]	Zhao QC, Yuan WH, Qu JQ et al. Optical fiber-integrated metasurfaces: an emerging platform for multiple optical applications. Nanomaterials (Basel) 12 , 793 (2022). Google Scholar
[256]	Pahlevaninezhad M, Huang YW, Pahlevani M et al. Metasurface-based bijective illumination collection imaging provides high-resolution tomography in three dimensions. Nat Photonics 16, 203–211 (2022). DOI: 10.1038/s41566-022-00956-6 CrossRef Google Scholar
[257]	Fröch JE, Huang LC, Tanguy QAA et al. Real time full-color imaging in a meta-optical fiber endoscope. eLight 3, 13 (2023). DOI: 10.1186/s43593-023-00044-4 CrossRef Google Scholar
[258]	Hariri LP, Villiger M, Applegate MB et al. Seeing beyond the bronchoscope to increase the diagnostic yield of bronchoscopic biopsy. Am J Respir Crit Care Med 187, 125–129 (2013). DOI: 10.1164/rccm.201208-1483OE CrossRef Google Scholar
[259]	Adams DC, Hariri LP, Miller AJ et al. Birefringence microscopy platform for assessing airway smooth muscle structure and function in vivo. Sci Transl Med 8, 359ra131 (2016). Google Scholar
[260]	Nadkarni SK, Pierce MC, Park BH et al. Measurement of collagen and smooth muscle cell content in atherosclerotic plaques using polarization-sensitive optical coherence tomography. J Am Coll Cardiol 49, 1474–1481 (2007). DOI: 10.1016/j.jacc.2006.11.040 CrossRef Google Scholar
[261]	Chia YH, Liao WH, Vyas S et al. In vivo intelligent fluorescence endo‐microscopy by varifocal meta‐device and deep learning. Adv Sci 11, 2307837 (2024). DOI: 10.1002/advs.202307837 CrossRef Google Scholar
[262]	Chu CH, Vyas S, Luo Y et al. Recent developments in biomedical applications of metasurface optics. APL Photonics 9, 030901 (2024). DOI: 10.1063/5.0190758 CrossRef Google Scholar
[263]	Gupta J, Das P, Bhattacharjee R et al. Enhancing signal-to-noise ratio of clinical 1.5T MRI using metasurface-inspired flexible wraps. Appl Phys A 129, 725 (2023). DOI: 10.1007/s00339-023-06962-x CrossRef Google Scholar
[264]	Brown MA, Semelka RC. MRI: Basic Principles and Applications (John Wiley & Sons, 2011). Google Scholar
[265]	Plewes DB, Kucharczyk W. Physics of MRI: a primer. J Magn Reson Imaging 35, 1038–1054 (2012). DOI: 10.1002/jmri.23642 CrossRef Google Scholar
[266]	Van Reeth E, Tham IWK, Tan CH et al. Super‐resolution in magnetic resonance imaging: a review. Concepts Magn Reson Part A 40, 306–325 (2012). Google Scholar
[267]	Voormolen EH, Diederen SJH, Woerdeman P et al. Implications of extracranial distortion in ultra-high-field magnetic resonance imaging for image-guided cranial neurosurgery. World Neurosurg 126, e250–e258 (2019). DOI: 10.1016/j.wneu.2019.02.028 CrossRef Google Scholar
[268]	Li ZP, Tian X, Qiu CW et al. Metasurfaces for bioelectronics and healthcare. Nat Electron 4, 382–391 (2021). DOI: 10.1038/s41928-021-00589-7 CrossRef Google Scholar
[269]	Slobozhanyuk AP, Poddubny AN, Raaijmakers AJE et al. Enhancement of magnetic resonance imaging with metasurfaces. Adv Mater 28, 1832–1838 (2016). DOI: 10.1002/adma.201504270 CrossRef Google Scholar
[270]	Stoja E, Konstandin S, Philipp D et al. Improving magnetic resonance imaging with smart and thin metasurfaces. Sci Rep 11, 16179 (2021). DOI: 10.1038/s41598-021-95420-w CrossRef Google Scholar
[271]	Kretov EI, Shchelokova AV, Slobozhanyuk AP. Impact of wire metasurface eigenmode on the sensitivity enhancement of MRI system. Appl Phys Lett 112, 033501 (2018). DOI: 10.1063/1.5013319 CrossRef Google Scholar
[272]	Zhao XG, Duan GW, Wu K et al. Intelligent metamaterials based on nonlinearity for magnetic resonance imaging. Adv Mater 31, 1905461 (2019). DOI: 10.1002/adma.201905461 CrossRef Google Scholar
[273]	Corneanu CA, Simón MO, Cohn JF et al. Survey on RGB, 3D, thermal, and multimodal approaches for facial expression recognition: History, trends, and affect-related applications. IEEE Trans Pattern Anal 38, 1548–1568 (2016). DOI: 10.1109/TPAMI.2016.2515606 CrossRef Google Scholar
[274]	Colburn S, Majumdar A. Single-shot three-dimensional imaging with a metasurface depth camera. arXiv preprint arXiv: 1910.12111 (2019). https://arxiv.org/abs/1910.12111 Google Scholar
[275]	Tsalakanidou F, Malassiotis S. Real-time 2D+ 3D facial action and expression recognition. Pattern Recognit 43, 1763–1775 (2010). DOI: 10.1016/j.patcog.2009.12.009 CrossRef Google Scholar
[276]	Sun LF, Wang ZR, Jiang JB et al. In-sensor reservoir computing for language learning via two-dimensional memristors. Sci Adv 7, eabg1455 (2021). DOI: 10.1126/sciadv.abg1455 CrossRef Google Scholar
[277]	Kwon JM, Yang SP, Jeong KH. Stereoscopic facial imaging for pain assessment using rotational offset microlens arrays based structured illumination. Micro Nano Syst Lett 9, 11 (2021). DOI: 10.1186/s40486-021-00139-y CrossRef Google Scholar
[278]	Imaoka H, Hashimoto H, Takahashi K et al. The future of biometrics technology: from face recognition to related applications. APSIPA Trans Signal Inf Process 10, e9 (2021). Google Scholar
[279]	Woodward Jr JD, Horn C, Gatune J et al. Biometrics: A Look at Facial Recognition (RAND, Santa Monica, 2003). Google Scholar
[280]	Du MY. Mobile payment recognition technology based on face detection algorithm. Concurr Comput Pract Exper 30, e4655 (2018). DOI: 10.1002/cpe.4655 CrossRef Google Scholar
[281]	Li ZL, Dai Q, Mehmood MQ et al. Full-space cloud of random points with a scrambling metasurface. Light Sci Appl 7, 63 (2018). DOI: 10.1038/s41377-018-0064-3 CrossRef Google Scholar
[282]	Xie YY, Ni PN, Wang QH et al. Metasurface-integrated vertical cavity surface-emitting lasers for programmable directional lasing emissions. Nat Nanotechnol 15, 125–130 (2020). DOI: 10.1038/s41565-019-0611-y CrossRef Google Scholar
[283]	Hu T, Zhong QZ, Li NX et al. CMOS-compatible a-Si metalenses on a 12-inch glass wafer for fingerprint imaging. Nanophotonics 9, 823–830 (2020). DOI: 10.1515/nanoph-2019-0470 CrossRef Google Scholar
[284]	Grew N. NOTES of the WEEK. Google Scholar
[285]	Galbally J, Haraksim R, Beslay L. A study of age and ageing in fingerprint biometrics. IEEE Trans Inf Foren Sec 14, 1351–1365 (2019). DOI: 10.1109/TIFS.2018.2878160 CrossRef Google Scholar
[286]	Yager N, Amin A. Fingerprint classification: a review. Pattern Anal Appl 7, 77–93 (2004). DOI: 10.1007/s10044-004-0204-7 CrossRef Google Scholar
[287]	Jain AK, Cao K, Arora SS. Recognizing infants and toddlers using fingerprints: Increasing the vaccination coverage. In Proceedings of IEEE International Joint Conference on Biometrics 1–8 (IEEE, 2014); http://doi.org/10.1109/BTAS.2014.6996252. Google Scholar
[288]	Lee HC, Gaensslen RE. Advances in Fingerprint Technology 2nd ed (CRC Press, Boca Raton, 2001). Google Scholar
[289]	Yang WC, Wang S, Hu JK et al. Security and accuracy of fingerprint-based biometrics: a review. Symmetry 11, 141 (2019). DOI: 10.3390/sym11020141 CrossRef Google Scholar
[290]	Uhl A, Wild P. Comparing verification performance of kids and adults for fingerprint, palmprint, hand-geometry and digitprint biometrics. In Proceedings of the 2009 IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems 1–6 (IEEE, 2009); http://doi.org/10.1109/BTAS.2009.5339069. Google Scholar
[291]	Oh DK, Lee T, Ko B et al. Nanoimprint lithography for high-throughput fabrication of metasurfaces. Front Optoelectron 14, 229–251 (2021). DOI: 10.1007/s12200-021-1121-8 CrossRef Google Scholar

View full references list

Cited By

Cited by

Periodical cited type(19)

1.	Ma, H., Shi, P., Yi, Z. A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks. Materials, 2025, 18(11): 2601. DOI:10.3390/ma18112601
2.	Zhang, B., Liu, M., Huang, Y. et al. Highly tunable rotationally symmetric multi-band terahertz absorber with enhanced sensing capabilities. Dalton Transactions, 2025, 54(22): 8993-8999. DOI:10.1039/d5dt00772k
3.	Ai, Z., Liu, H., Cheng, S. et al. Four peak and high angle tilted insensitive surface plasmon resonance graphene absorber based on circular etching square window. Journal of Physics D Applied Physics, 2025, 58(18): 185305. DOI:10.1088/1361-6463/adc467
4.	Lin, J., Guo, Z., Zhang, B. A variety of adjustable terahertz absorbers based on bulk Dirac semi-metal. Physica Scripta, 2025, 100(5): 055942. DOI:10.1088/1402-4896/adc848
5.	Zhang, S., Chen, K., Sun, T. et al. Highly Sensitive and Tunable Graphene Metamaterial Perfect Absorber in the Near-Terahertz Band. Coatings, 2025, 15(5): 512. DOI:10.3390/coatings15050512
6.	Wang, Y., Liu, Z., Zhou, F. et al. Perfect absorption properties of a near-infrared super-surface perfect absorber based on a multilayer subwavelength array structure. Physics Letters Section A General Atomic and Solid State Physics, 2025. DOI:10.1016/j.physleta.2025.130395
7.	Jo, Y., Park, H., Lee, S. et al. Spectral Hadamard microscopy with metasurface-based patterned illumination. Nanophotonics, 2025, 14(8): 1171-1183. DOI:10.1515/nanoph-2024-0587
8.	Khodadadi, B., Rezaei, P., Hadipour, S. Accurate graphene-based absorber for slight leakage detection of Radon and chloroform air-pollution. Results in Physics, 2025. DOI:10.1016/j.rinp.2025.108196
9.	Wang, X., He, X., Yang, H. et al. Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency. Molecules, 2025, 30(8): 1688. DOI:10.3390/molecules30081688
10.	Zhou, J., Sun, X., Xu, J. et al. Versatile Tunable Terahertz Absorption Device Based on Bulk Dirac Semimetals and Graphene. Molecules, 2025, 30(5): 999. DOI:10.3390/molecules30050999
11.	Wan, Y., Sun, T., Song, Q. et al. A five-peaks graphene-based metamaterial terahertz absorber with dynamic tunability for sensing application. Diamond and Related Materials, 2025. DOI:10.1016/j.diamond.2025.112090
12.	Li, Z., Cheng, S., Zhang, H. et al. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Physics Letters Section A General Atomic and Solid State Physics, 2025. DOI:10.1016/j.physleta.2025.130262
13.	Wang, X., He, X., Tang, C. et al. A terahertz band multifunctional metamaterial transmission-absorption switching device based on vanadium dioxide. Dalton Transactions, 2025, 54(13): 5494-5501. DOI:10.1039/d5dt00153f
14.	Yuan, H., Wang, Z., Sun, T. et al. Ultra-broadband absorber and near-perfect thermal emitter based on multi-layered grating structure design. Energy, 2025. DOI:10.1016/j.energy.2025.134594
15.	He, Z., Fang, D., Yi, Y. Design of a Tunable Metamaterial Absorption Device with an Absorption Band Covering the Mid-Infrared Atmospheric Window. Photonics, 2025, 12(2): 148. DOI:10.3390/photonics12020148
16.	Yi, Z., Yao, X., Song, Q. et al. Ultra High Efficiency Solar Capture Device Based on InAs Nanoring Microstructure. Coatings, 2025, 15(2): 243. DOI:10.3390/coatings15020243
17.	Zheng, Y., Wang, Z., Song, Q. et al. Thermal management broadband-emitting device based on VO2 applied in the mid-infrared band. Dalton Transactions, 2025, 54(8): 3157-3164. DOI:10.1039/d4dt03422h
18.	Wang, J., Song, Q., Yang, H. et al. Infrared band ultra-wideband metamaterial absorption device based on cylindrical multiscale resonator. Physical Chemistry Chemical Physics, 2025. DOI:10.1039/d5cp00968e
19.	Barulina, E., Nguyen, D.D., Shuklin, F. et al. Dual-Wavelength On-Chip Integrated Metalens for Epi-Fluorescence Single-Molecule Sensing. Sensors, 2024, 24(23): 7781. DOI:10.3390/s24237781

Other cited types(0)

Author Information

Author Information
- Yongjae Jo On this Site On Google Scholar
  - Department of Biophysics, Institute of Quantum Biophysics, Sungkyunkwan University, Suwon 16419, Republic of Korea
- Hyemi Park On this Site On Google Scholar
  - Department of Biophysics, Institute of Quantum Biophysics, Sungkyunkwan University, Suwon 16419, Republic of Korea
  - Department of Intelligent Precision Healthcare Convergence, Sungkyunkwan University, Suwon 16419, Republic of Korea
- Hyeyoung Yoon On this Site On Google Scholar
  - Department of Intelligent Precision Healthcare Convergence, Sungkyunkwan University, Suwon 16419, Republic of Korea
  - Center for Quantum Information, Korea Institute of Science and Technology (KIST), Seoul 02792, Republic of Korea
- Corresponding author: Inki Kim, inki.kim@skku.edu On this Site On Google Scholar
  I Kim, E-mail: inki.kim@skku.edu
  - Department of Biophysics, Institute of Quantum Biophysics, Sungkyunkwan University, Suwon 16419, Republic of Korea
  - Department of Intelligent Precision Healthcare Convergence, Sungkyunkwan University, Suwon 16419, Republic of Korea
^†These authors contributed equally to this work

Author contributions

I. Kim conceived the study. Y. Jo, H. Park and H. Yoon wrote the manuscript. I. Kim supervised the study.

Copyright

Open Access. © The Author(s). This article is licensed under a Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

About this Article

About this Article
DOI: 10.29026/oea.2024.240122

Cite this Article

Yongjae Jo, Hyemi Park, Hyeyoung Yoon, et al. Advanced biological imaging techniques based on metasurfaces. Opto-Electronic Advances 7, 240122 (2024). DOI: 10.29026/oea.2024.240122

Yongjae Jo, Hyemi Park, Hyeyoung Yoon, et al. Advanced biological imaging techniques based on metasurfaces. Opto-Electronic Advances 7, 240122 (2024). DOI: 10.29026/oea.2024.240122

Download Citation
Article History
- Received Date May 21, 2024
- Accepted Date August 18, 2024
- Available Online October 30, 2024
- Published Date December 15, 2024
Article Metrics

Article Views(4385) PDF Downloads(266)
Share:

Related Articles
- On-chip metasurfaces unlock efficient vector terahertz beams
  
  Jitao Ji, Tao Li, Shining Zhu
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2025.250158
- Phase reconstruction via metasurface-integrated quantum analog operation
  
  Qiuying Li, Minggui Liang, Shuoqing Liu, Jiawei Liu, Shizhen Chen, Shuangchun Wen, Hailu Luo
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2025.240239
- Focus control of wide-angle metalens based on digitally encoded metasurface
  
  Yi Chen, Simeng Zhang, Ying Tian, Chenxia Li, Wenlong Huang, Yixin Liu, Yongxing Jin, Bo Fang, Zhi Hong, Xufeng Jing
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2024.240095
- Advancing nonlinear nanophotonics: harnessing membrane metasurfaces for third-harmonic generation and imaging
  
  Mingbo Pu, Xiangang Luo
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2023.230153
- Planar peristrophic multiplexing metasurfaces
  
  Jia Chen, Dapeng Wang, Guangyuan Si, Siew Lang Teo, Qian Wang, Jiao Lin
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2023.220141
- Crosstalk-free achromatic full Stokes imaging polarimetry metasurface enabled by polarization-dependent phase optimization
  
  Yaxin Zhang, Mingbo Pu, Jinjin Jin, Xinjian Lu, Yinghui Guo, Jixiang Cai, Fei Zhang, Yingli Ha, Qiong He, Mingfeng Xu, Xiong Li, Xiaoliang Ma, Xiangang Luo
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2022.220058
- Photoluminescence control by hyperbolic metamaterials and metasurfaces: a review
  
  Leonid Yu. Beliaev, Osamu Takayama, Pavel N. Melentiev, Andrei V. Lavrinenko
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2021.210031
- Ultra-high extinction-ratio light modulation by electrically tunable metasurface using dual epsilon-near-zero resonances
  
  Arash Nemati, Qian Wang, Norman Soo Seng Ang, Weide Wang, Minghui Hong, Jinghua Teng
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2021.200088
- Polarization multiplexing for double images display
  
  Jinying Guo, Teng Wang, Baogang Quan, Huan Zhao, Changzhi Gu, Junjie Li, Xinke Wang, Guohai Situ, Yan Zhang
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2019.180029
- Tunable and reconfigurable metasurfaces and metadevices
  
  Arash Nemati, Qian Wang, Minghui Hong, Jinghua Teng
  
  Opto-Electronic Advances, DOI: 10.29026/oea.2018.180009

Article Contents
Figures/Tables
References

View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint

[1]	Avrutsky I, Chaganti K, Salakhutdinov I et al. Concept of a miniature optical spectrometer using integrated optical and micro-optical components. Appl Opt 45, 7811–7817 (2006). DOI: 10.1364/AO.45.007811 CrossRef Google Scholar
[2]	Khorasaninejad M, Capasso F. Metalenses: versatile multifunctional photonic components. Science 358, eaam8100 (2017). DOI: 10.1126/science.aam8100 CrossRef Google Scholar
[3]	Khorasaninejad M, Chen WT, Devlin RC et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016). DOI: 10.1126/science.aaf6644 CrossRef Google Scholar
[4]	Ni XJ, Ishii S, Kildishev AV et al. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light Sci Appl 2, e72 (2013). DOI: 10.1038/lsa.2013.28 CrossRef Google Scholar
[5]	Kim I, Jang J, Kim G et al. Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform. Nat Commun 12, 3614 (2021). DOI: 10.1038/s41467-021-23814-5 CrossRef Google Scholar
[6]	Kim I, Kim WS, Kim K et al. Holographic metasurface gas sensors for instantaneous visual alarms. Sci Adv 7, eabe9943 (2021). DOI: 10.1126/sciadv.abe9943 CrossRef Google Scholar
[7]	Paniagua-Dominguez R, Yu YF, Khaidarov E et al. A metalens with a near-unity numerical aperture. Nano Lett 18, 2124–2132 (2018). DOI: 10.1021/acs.nanolett.8b00368 CrossRef Google Scholar
[8]	Liang HW, Lin QL, Xie XS et al. Ultrahigh numerical aperture metalens at visible wavelengths. Nano Lett 18, 4460–4466 (2018). DOI: 10.1021/acs.nanolett.8b01570 CrossRef Google Scholar
[9]	Chung H, Miller OD. High-NA achromatic metalenses by inverse design. Opt Express 28, 6945–6965 (2020). DOI: 10.1364/OE.385440 CrossRef Google Scholar
[10]	Zhang SY, Wong CL, Zeng SW et al. Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective. Nanophotonics 10, 259–293 (2021). Google Scholar
[11]	Nguyen DD, Lee S, Kim I. Recent advances in metaphotonic biosensors. Biosensors 13, 631 (2023). DOI: 10.3390/bios13060631 CrossRef Google Scholar
[12]	Chen WT, Zhu AY, Sanjeev V et al. A broadband achromatic metalens for focusing and imaging in the visible. Nat Nanotechnol 13, 220–226 (2018). DOI: 10.1038/s41565-017-0034-6 CrossRef Google Scholar
[13]	Lin RJ, Su VC, Wang SM et al. Achromatic metalens array for full-colour light-field imaging. Nat Nanotechnol 14, 227–231 (2019). DOI: 10.1038/s41565-018-0347-0 CrossRef Google Scholar
[14]	Rho J, Ye ZL, Xiong Y et al. Spherical hyperlens for two-dimensional sub-diffractional imaging at visible frequencies. Nat Commun 1, 143 (2010). DOI: 10.1038/ncomms1148 CrossRef Google Scholar
[15]	Lee D, Kim YD, Kim M et al. Realization of wafer-scale hyperlens device for sub-diffractional biomolecular imaging. ACS Photonics 5, 2549–2554 (2018). DOI: 10.1021/acsphotonics.7b01182 CrossRef Google Scholar
[16]	Lee YU, Zhao JX, Ma Q et al. Metamaterial assisted illumination nanoscopy via random super-resolution speckles. Nat Commun 12, 1559 (2021). DOI: 10.1038/s41467-021-21835-8 CrossRef Google Scholar
[17]	Masuda S, Kuboki T, Kidoaki S et al. High axial and lateral resolutions on self-assembled gold nanoparticle metasurfaces for live-cell imaging. ACS Appl Nano Mater 3, 11135–11142 (2020). DOI: 10.1021/acsanm.0c02300 CrossRef Google Scholar
[18]	Huo PC, Zhang C, Zhu WQ et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett 20, 2791–2798 (2020). DOI: 10.1021/acs.nanolett.0c00471 CrossRef Google Scholar
[19]	Wang XW, Wang H, Wang JL et al. Single-shot isotropic differential interference contrast microscopy. Nat Commun 14, 2063 (2023). DOI: 10.1038/s41467-023-37606-6 CrossRef Google Scholar
[20]	Shi FH, Wen J, Lei DY. High-efficiency, large-area lattice light-sheet generation by dielectric metasurfaces. Nanophotonics 9, 4043–4051 (2020). DOI: 10.1515/nanoph-2020-0227 CrossRef Google Scholar
[21]	Luo Y, Tseng ML, Vyas S et al. Meta-lens light-sheet fluorescence microscopy for in vivo imaging. Nanophotonics 11, 1949–1959 (2022). DOI: 10.1515/nanoph-2021-0748 CrossRef Google Scholar
[22]	Wang CH, Chen QM, Liu HL et al. Miniature two-photon microscopic imaging using dielectric metalens. Nano Lett 23, 8256–8263 (2023). DOI: 10.1021/acs.nanolett.3c02439 CrossRef Google Scholar
[23]	Barulin A, Park H, Park B et al. Dual-wavelength UV-visible metalens for multispectral photoacoustic microscopy: a simulation study. Photoacoustics 32, 100545 (2023). DOI: 10.1016/j.pacs.2023.100545 CrossRef Google Scholar
[24]	Song W, Guo CK, Zhao YT et al. Ultraviolet metasurface-assisted photoacoustic microscopy with great enhancement in DOF for fast histology imaging. Photoacoustics 32, 100525 (2023). DOI: 10.1016/j.pacs.2023.100525 CrossRef Google Scholar
[25]	Pahlevaninezhad H, Khorasaninejad M, Huang YW et al. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat Photonics 12, 540–547 (2018). DOI: 10.1038/s41566-018-0224-2 CrossRef Google Scholar
[26]	Schmidt R, Slobozhanyuk A, Belov P et al. Flexible and compact hybrid metasurfaces for enhanced ultra high field in vivo magnetic resonance imaging. Sci Rep 7, 1678 (2017). DOI: 10.1038/s41598-017-01932-9 CrossRef Google Scholar
[27]	Lassalle E, Mass TWW, Eschimese D et al. Imaging properties of large field-of-view quadratic metalenses and their applications to fingerprint detection. ACS Photonics 8, 1457–1468 (2021). DOI: 10.1021/acsphotonics.1c00237 CrossRef Google Scholar
[28]	Hsu WC, Chang CH, Hong YH et al. Metasurface- and PCSEL-based structured light for monocular depth perception and facial recognition. Nano Lett 24, 1808–1815 (2024). DOI: 10.1021/acs.nanolett.3c05002 CrossRef Google Scholar
[29]	Yu NF, Genevet P, Kats MA et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011). DOI: 10.1126/science.1210713 CrossRef Google Scholar
[30]	Hu J, Bandyopadhyay S, Liu YH et al. A review on metasurface: from principle to smart metadevices. Front Phys 8, 586087 (2021). DOI: 10.3389/fphy.2020.586087 CrossRef Google Scholar
[31]	Yu NF, Capasso F. Flat optics with designer metasurfaces. Nat Mater 13, 139–150 (2014). DOI: 10.1038/nmat3839 CrossRef Google Scholar
[32]	Khorasaninejad M, Zhu AY, Roques-Carmes C et al. Polarization-insensitive metalenses at visible wavelengths. Nano Lett 16, 7229–7234 (2016). DOI: 10.1021/acs.nanolett.6b03626 CrossRef Google Scholar
[33]	Khorasaninejad M, Chen WT, Oh J et al. Super-dispersive off-axis meta-lenses for compact high resolution spectroscopy. Nano Lett 16, 3732–3737 (2016). DOI: 10.1021/acs.nanolett.6b01097 CrossRef Google Scholar
[34]	Mueller JPB, Rubin NA, Devlin RC et al. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys Rev Lett 118, 113901 (2017). DOI: 10.1103/PhysRevLett.118.113901 CrossRef Google Scholar
[35]	Cong LQ, Xu NN, Zhang WL et al. Polarization control in terahertz metasurfaces with the lowest order rotational symmetry. Adv Opt Mater 3, 1176–1183 (2015). DOI: 10.1002/adom.201500100 CrossRef Google Scholar
[36]	Chen XZ, Huang LL, Mühlenbernd H et al. Dual-polarity plasmonic metalens for visible light. Nat Commun 3, 1198 (2012). DOI: 10.1038/ncomms2207 CrossRef Google Scholar
[37]	Arbabi A, Horie Y, Bagheri M et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat Nanotechnol 10, 937–943 (2015). DOI: 10.1038/nnano.2015.186 CrossRef Google Scholar
[38]	Jiang SC, Xiong X, Hu YS et al. High-efficiency generation of circularly polarized light via symmetry-induced anomalous reflection. Phys Rev B 91, 125421 (2015). DOI: 10.1103/PhysRevB.91.125421 CrossRef Google Scholar
[39]	Huang LL, Chen XZ, Mühlenbernd H et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett 12, 5750–5755 (2012). DOI: 10.1021/nl303031j CrossRef Google Scholar
[40]	Moon SW, Lee C, Yang Y et al. Tutorial on metalenses for advanced flat optics: design, fabrication, and critical considerations. J Appl Phys 131, 091101 (2022). DOI: 10.1063/5.0078804 CrossRef Google Scholar
[41]	Luo WJ, Sun SL, Xu HX et al. Transmissive ultrathin pancharatnam-berry metasurfaces with nearly 100% efficiency. Phys Rev Appl 7, 044033 (2017). DOI: 10.1103/PhysRevApplied.7.044033 CrossRef Google Scholar
[42]	Fu X, Liang HW, Li JT. Metalenses: from design principles to functional applications. Front Optoelectron 14, 170–186 (2021). DOI: 10.1007/s12200-021-1201-9 CrossRef Google Scholar
[43]	Kim J, Li YM, Miskiewicz MN et al. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica 2, 958–964 (2015). DOI: 10.1364/OPTICA.2.000958 CrossRef Google Scholar
[44]	Wen DD, Yue FY, Li GX et al. Helicity multiplexed broadband metasurface holograms. Nat Commun 6, 8241 (2015). DOI: 10.1038/ncomms9241 CrossRef Google Scholar
[45]	Chen WT, Khorasaninejad M, Zhu AY et al. Generation of wavelength-independent subwavelength Bessel beams using metasurfaces. Light Sci Appl 6, e16259 (2017). Google Scholar
[46]	Xu R, Chen P, Tang J et al. Perfect higher-order Poincaré sphere beams from digitalized geometric phases. Phys Rev Appl 10, 034061 (2018). DOI: 10.1103/PhysRevApplied.10.034061 CrossRef Google Scholar
[47]	Jeon D, Shin K, Moon SW et al. Recent advancements of metalenses for functional imaging. Nano Converg 10, 24 (2023). DOI: 10.1186/s40580-023-00372-8 CrossRef Google Scholar
[48]	Liu MK, Choi DY. Extreme Huygens’ metasurfaces based on quasi-bound states in the continuum. Nano Lett 18, 8062–8069 (2018). DOI: 10.1021/acs.nanolett.8b04774 CrossRef Google Scholar
[49]	Kim G, Kim Y, Yun J et al. Metasurface-driven full-space structured light for three-dimensional imaging. Nat Commun 13, 5920 (2022). DOI: 10.1038/s41467-022-32117-2 CrossRef Google Scholar
[50]	Wang YJ, Chen QM, Yang WH et al. High-efficiency broadband achromatic metalens for near-IR biological imaging window. Nat Commun 12, 5560 (2021). DOI: 10.1038/s41467-021-25797-9 CrossRef Google Scholar
[51]	Chen WT, Zhu AY, Sisler J et al. A broadband achromatic polarization-insensitive metalens consisting of anisotropic nanostructures. Nat Commun 10, 355 (2019). DOI: 10.1038/s41467-019-08305-y CrossRef Google Scholar
[52]	Heiden JT, Jang MS. Design framework for polarization-insensitive multifunctional achromatic metalenses. Nanophotonics 11, 583–591 (2022). DOI: 10.1515/nanoph-2021-0638 CrossRef Google Scholar
[53]	Faraji-Dana M, Arbabi E, Arbabi A et al. Compact folded metasurface spectrometer. Nat Commun 9, 4196 (2018). DOI: 10.1038/s41467-018-06495-5 CrossRef Google Scholar
[54]	Cai GY, Li YH, Zhang Y et al. Compact angle-resolved metasurface spectrometer. Nat Mater 23, 71–78 (2024). DOI: 10.1038/s41563-023-01710-1 CrossRef Google Scholar
[55]	Wang RX, Ansari MA, Ahmed H et al. Compact multi-foci metalens spectrometer. Light Sci Appl 12, 103 (2023). DOI: 10.1038/s41377-023-01148-9 CrossRef Google Scholar
[56]	Faraji-Dana M, Arbabi E, Arbabi A et al. Folded planar metasurface spectrometer. In Proceedings of 2018 Conference on Lasers and Electro-Optics (CLEO) 1–2 (IEEE, 2018). Google Scholar
[57]	Liu WQ, Deng L, Li SF et al. High transmittance and broadband group delay metasurface element in Ka band. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT) 669–671 (IEEE, 2021); http://doi.org/10.1109/ICEICT53123.2021.9531170. Google Scholar
[58]	Miyamaru F, Morita H, Nishiyama Y et al. Ultrafast optical control of group delay of narrow-band terahertz waves. Sci Rep 4, 4346 (2014). DOI: 10.1038/srep04346 CrossRef Google Scholar
[59]	Jiang L, Li XZ, Wu QX et al. Neural network enabled metasurface design for phase manipulation. Opt Express 29, 2521–2528 (2021). DOI: 10.1364/OE.413079 CrossRef Google Scholar
[60]	Chen MZ, Cheng Q, Xia F et al. Metasurface‐based spatial phasers for analogue signal processing. Adv Opt Mater 8, 2000128 (2020). DOI: 10.1002/adom.202000128 CrossRef Google Scholar
[61]	Tsilipakos O, Koschny T, Soukoulis CM. Antimatched electromagnetic metasurfaces for broadband arbitrary phase manipulation in reflection. ACS Photonics 5, 1101–1107 (2018). DOI: 10.1021/acsphotonics.7b01415 CrossRef Google Scholar
[62]	Trubetskov MK, Von Pechmann M, Angelov IB et al. Measurements of the group delay and the group delay dispersion with resonance scanning interferometer. Opt Express 21, 6658–6669 (2013). DOI: 10.1364/OE.21.006658 CrossRef Google Scholar
[63]	Song NT, Xu NX, Shan DZ et al. Broadband achromatic metasurfaces for longwave infrared applications. Nanomaterials 11, 2760 (2021). DOI: 10.3390/nano11102760 CrossRef Google Scholar
[64]	He YL, Song BX, Tang J. Optical metalenses: fundamentals, dispersion manipulation, and applications. Front Optoelectron 15, 24 (2022). DOI: 10.1007/s12200-022-00017-4 CrossRef Google Scholar
[65]	Pan Y, Neuss S, Leifert A et al. Size‐dependent cytotoxicity of gold nanoparticles. Small 3, 1941–1949 (2007). DOI: 10.1002/smll.200700378 CrossRef Google Scholar
[66]	Gonçalves MR, Minassian H, Melikyan A. Plasmonic resonators: fundamental properties and applications. J Phys D Appl Phys 53, 443002 (2020). DOI: 10.1088/1361-6463/ab96e9 CrossRef Google Scholar
[67]	Xu Q, Zhang XQ, Xu YH et al. Plasmonic metalens based on coupled resonators for focusing of surface plasmons. Sci Rep 6, 37861 (2016). DOI: 10.1038/srep37861 CrossRef Google Scholar
[68]	Autore M, Hillenbrand R. What momentum mismatch. Nat Nanotechnol 14, 308–309 (2019). DOI: 10.1038/s41565-019-0390-5 CrossRef Google Scholar
[69]	Kim K, Oh Y, Ma K et al. Plasmon-enhanced total-internal-reflection fluorescence by momentum-mismatched surface nanostructures. Opt Lett 34, 3905–3907 (2009). DOI: 10.1364/OL.34.003905 CrossRef Google Scholar
[70]	Qin LS, Chen X, Zhang LL et al. Design, fabrication and testing of gain SPR sensor chip. J Phys Conf Ser 1209, 012006 (2019). DOI: 10.1088/1742-6596/1209/1/012006 CrossRef Google Scholar
[71]	Petryayeva E, Krull UJ. Localized surface plasmon resonance: nanostructures, bioassays and biosensing—A review. Anal Chim Acta 706, 8–24 (2011). DOI: 10.1016/j.aca.2011.08.020 CrossRef Google Scholar
[72]	Palermo G, Lininger A, Guglielmelli A et al. All-optical tunability of metalenses permeated with liquid crystals. ACS nano 16, 16539–16548 (2022). DOI: 10.1021/acsnano.2c05887 CrossRef Google Scholar
[73]	Park S, Hahn JW, Lee JY. Doubly resonant metallic nanostructure for high conversion efficiency of second harmonic generation. Opt Express 20, 4856–4870 (2012). DOI: 10.1364/OE.20.004856 CrossRef Google Scholar
[74]	Damgaard-Carstensen C, Ding F, Meng C et al. Demonstration of> 2π reflection phase range in optical metasurfaces based on detuned gap-surface plasmon resonators. Sci Rep 10, 19031 (2020). DOI: 10.1038/s41598-020-75931-8 CrossRef Google Scholar
[75]	Yao K, Liu YM. Plasmonic metamaterials. Nanotechnol Rev 3, 177–210 (2014). Google Scholar
[76]	Tong XC. Plasmonic metamaterials and metasurfaces. In Tong XC. Functional Metamaterials and Metadevices 129–153 (Springer, Cham, 2018). Google Scholar
[77]	Christopher P, Xin HL, Linic S. Visible-light-enhanced catalytic oxidation reactions on plasmonic silver nanostructures. Nat Chem 3, 467–472 (2011). DOI: 10.1038/nchem.1032 CrossRef Google Scholar
[78]	Barnard ES, White JS, Chandran A et al. Spectral properties of plasmonic resonator antennas. Opt Express 16, 16529–16537 (2008). DOI: 10.1364/OE.16.016529 CrossRef Google Scholar
[79]	Sun SL, He Q, Hao JM et al. Electromagnetic metasurfaces: physics and applications. Adv Opt Photonics 11, 380–479 (2019). DOI: 10.1364/AOP.11.000380 CrossRef Google Scholar
[80]	Pors A, Albrektsen O, Radko IP et al. Gap plasmon-based metasurfaces for total control of reflected light. Sci Rep 3, 2155 (2013). DOI: 10.1038/srep02155 CrossRef Google Scholar
[81]	Ding F, Yang YQ, Deshpande RA et al. A review of gap-surface plasmon metasurfaces: fundamentals and applications. Nanophotonics 7, 1129–1156 (2018). DOI: 10.1515/nanoph-2017-0125 CrossRef Google Scholar
[82]	Pors A, Bozhevolnyi SI. Plasmonic metasurfaces for efficient phase control in reflection. Opt Express 21, 27438–27451 (2013). DOI: 10.1364/OE.21.027438 CrossRef Google Scholar
[83]	Pors A, Nielsen MG, Eriksen RL et al. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces. Nano Lett 13, 829–834 (2013). DOI: 10.1021/nl304761m CrossRef Google Scholar
[84]	Boroviks S, Deshpande RA, Mortensen NA et al. Multifunctional metamirror: polarization splitting and focusing. ACS Photonics 5, 1648–1653 (2018). DOI: 10.1021/acsphotonics.7b01091 CrossRef Google Scholar
[85]	Cortés E, Wendisch FJ, Sortino L et al. Optical metasurfaces for energy conversion. Chem Rev 122, 15082–15176 (2022). DOI: 10.1021/acs.chemrev.2c00078 CrossRef Google Scholar
[86]	Linic S, Christopher P, Ingram DB. Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat Mater 10, 911–921 (2011). DOI: 10.1038/nmat3151 CrossRef Google Scholar
[87]	Gutruf P, Zou CJ, Withayachumnankul W et al. Mechanically tunable dielectric resonator metasurfaces at visible frequencies. Acs Nano 10, 133–141 (2016). DOI: 10.1021/acsnano.5b05954 CrossRef Google Scholar
[88]	Campione S, Basilio LI, Warne LK et al. Tailoring dielectric resonator geometries for directional scattering and Huygens’ metasurfaces. Opt Express 23, 2293–2307 (2015). DOI: 10.1364/OE.23.002293 CrossRef Google Scholar
[89]	Decker M, Staude I, Falkner M et al. High‐efficiency dielectric Huygens’ surfaces. Adv Opt Mater 3, 813–820 (2015). DOI: 10.1002/adom.201400584 CrossRef Google Scholar
[90]	Maier SA. Plasmonics: Fundamentals and Applications (Springer, New York, 2007). Google Scholar
[91]	Koshelev K, Kivshar Y. Dielectric resonant metaphotonics. ACS Photonics 8, 102–112 (2021). Google Scholar
[92]	Lin DM, Fan PY, Hasman E et al. Dielectric gradient metasurface optical elements. Science 345, 298–302 (2014). DOI: 10.1126/science.1253213 CrossRef Google Scholar
[93]	Devlin RC, Khorasaninejad M, Chen WT et al. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc Natl Acad Sci USA 113, 10473–10478 (2016). DOI: 10.1073/pnas.1611740113 CrossRef Google Scholar
[94]	Zhou SH, Shen ZX, Li XA et al. Liquid crystal integrated metalens with dynamic focusing property. Opt Lett 45, 4324–4327 (2020). DOI: 10.1364/OL.398601 CrossRef Google Scholar
[95]	Pan MY, Fu YF, Zheng MJ et al. Dielectric metalens for miniaturized imaging systems: progress and challenges. Light Sci Appl 11, 195 (2022). DOI: 10.1038/s41377-022-00885-7 CrossRef Google Scholar
[96]	Kerker M, Wang DS, Giles CL. Electromagnetic scattering by magnetic spheres. J Opt Soc Am 73, 765–767 (1983). DOI: 10.1364/JOSA.73.000765 CrossRef Google Scholar
[97]	Bukharin MM, Pecherkin VY, Ospanova AK et al. Transverse Kerker effect in all-dielectric spheroidal particles. Sci Rep 12, 7997 (2022). DOI: 10.1038/s41598-022-11733-4 CrossRef Google Scholar
[98]	Liu W, Kivshar YS. Generalized Kerker effects in nanophotonics and meta-optics [Invited]. Opt Express 26, 13085–13105 (2018). DOI: 10.1364/OE.26.013085 CrossRef Google Scholar
[99]	Liu WW, Li ZC, Cheng H et al. Dielectric resonance-based optical metasurfaces: from fundamentals to applications. iScience 23, 101868 (2020). DOI: 10.1016/j.isci.2020.101868 CrossRef Google Scholar
[100]	Genevet P, Capasso F, Aieta F et al. Recent advances in planar optics: from plasmonic to dielectric metasurfaces. Optica 4, 139–152 (2017). DOI: 10.1364/OPTICA.4.000139 CrossRef Google Scholar
[101]	Long S, McAllister M, Shen L. The resonant cylindrical dielectric cavity antenna. IEEE Trans Antennas Propag 31, 406–412 (1983). DOI: 10.1109/TAP.1983.1143080 CrossRef Google Scholar
[102]	Wang SW, Lai JJ, Wu T et al. Wide-band achromatic metalens for visible light by dispersion compensation method. J Phys D Appl Phys 50, 455101 (2017). DOI: 10.1088/1361-6463/aa8c90 CrossRef Google Scholar
[103]	Rytov S. Electromagnetic properties of a finely stratified medium. Sov Phys JEPT 2, 466–475 (1956). Google Scholar
[104]	Vo S, Fattal D, Sorin WV et al. Sub-wavelength grating lenses with a twist. IEEE Photonics Technol Lett 26, 1375–1378 (2014). DOI: 10.1109/LPT.2014.2325947 CrossRef Google Scholar
[105]	Arbabi A, Horie Y, Ball AJ et al. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat Commun 6, 7069 (2015). DOI: 10.1038/ncomms8069 CrossRef Google Scholar
[106]	Powell DA. Interference between the modes of an all-dielectric meta-atom. Phys Rev Appl 7, 034006 (2017). DOI: 10.1103/PhysRevApplied.7.034006 CrossRef Google Scholar
[107]	Wang Q, Rogers ETF, Gholipour B et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat Photonics 10, 60–65 (2016). DOI: 10.1038/nphoton.2015.247 CrossRef Google Scholar
[108]	Zhang YF, Fowler C, Liang JH et al. Electrically reconfigurable non-volatile metasurface using low-loss optical phase-change material. Nat Nanotechnol 16, 661–666 (2021). DOI: 10.1038/s41565-021-00881-9 CrossRef Google Scholar
[109]	Abdollahramezani S, Hemmatyar O, Taghinejad M et al. Electrically driven reprogrammable phase-change metasurface reaching 80% efficiency. Nat Commun 13, 1696 (2022). DOI: 10.1038/s41467-022-29374-6 CrossRef Google Scholar
[110]	Wang Y, Cui DJ, Wang Y et al. Electrically and thermally tunable multifunctional terahertz metasurface array. Phys Rev A 105, 033520 (2022). DOI: 10.1103/PhysRevA.105.033520 CrossRef Google Scholar
[111]	Shao ZW, Cao X, Luo HJ et al. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mater 10, 581–605 (2018). DOI: 10.1038/s41427-018-0061-2 CrossRef Google Scholar
[112]	Shalaginov MY, An SS, Zhang YF et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat Commun 12, 1225 (2021). DOI: 10.1038/s41467-021-21440-9 CrossRef Google Scholar
[113]	Zhang WH, Wu XQ, Li L et al. Fabrication of a VO₂-based tunable metasurface by electric-field scanning probe lithography with precise depth control. ACS Appl Mater Interfaces 15, 13517–13525 (2023). DOI: 10.1021/acsami.2c21935 CrossRef Google Scholar
[114]	Hashemi MRM, Yang SH, Wang TY et al. Electronically-controlled beam-steering through vanadium dioxide metasurfaces. Sci Rep 6, 35439 (2016). DOI: 10.1038/srep35439 CrossRef Google Scholar
[115]	King J, Wan CH, Park TJ et al. Electrically tunable VO₂–metal metasurface for mid-infrared switching, limiting and nonlinear isolation. Nat Photonics 18, 74–80 (2024). DOI: 10.1038/s41566-023-01324-8 CrossRef Google Scholar
[116]	Wan CH, Zhang Z, Woolf D et al. On the optical properties of thin‐film vanadium dioxide from the visible to the far infrared. Ann Phys 531, 1900188 (2019). DOI: 10.1002/andp.201900188 CrossRef Google Scholar
[117]	Chu F, Tian LL, Li R et al. Adaptive nematic liquid crystal lens array with resistive layer. Liq Cryst 47, 563–571 (2020). DOI: 10.1080/02678292.2019.1662502 CrossRef Google Scholar
[118]	Kang DH, Heo HS, Yang YH et al. Liquid crystal-integrated metasurfaces for an active photonic platform. Opto-Electron Adv 7, 230216 (2024). DOI: 10.29026/oea.2024.230216 CrossRef Google Scholar
[119]	Chang X, Pivnenko M, Shrestha P et al. Electrically tuned active metasurface towards metasurface-integrated liquid crystal on silicon (meta-LCoS) devices. Opt Express 31, 5378–5387 (2023). DOI: 10.1364/OE.483452 CrossRef Google Scholar
[120]	Ji YY, Fan F, Zhang X et al. Active terahertz anisotropy and dispersion engineering based on dual-frequency liquid crystal and dielectric metasurface. J Lightwave Technol 38, 4030–4036 (2020). Google Scholar
[121]	Rocco D, Carletti L, Caputo R et al. Switching the second harmonic generation by a dielectric metasurface via tunable liquid crystal. Opt Express 28, 12037–12046 (2020). DOI: 10.1364/OE.386776 CrossRef Google Scholar
[122]	Badloe T, Kim Y, Kim J et al. Bright-field and edge-enhanced imaging using an electrically tunable dual-mode metalens. ACS Nano 17, 14678–14685 (2023). DOI: 10.1021/acsnano.3c02471 CrossRef Google Scholar
[123]	Bosch M, Shcherbakov MR, Won K et al. Electrically actuated varifocal lens based on liquid-crystal-embedded dielectric metasurfaces. Nano Lett 21, 3849–3856 (2021). DOI: 10.1021/acs.nanolett.1c00356 CrossRef Google Scholar
[124]	Kamali SM, Arbabi A, Arbabi E et al. Decoupling optical function and geometrical form using conformal flexible dielectric metasurfaces. Nat Commun 7, 11618 (2016). DOI: 10.1038/ncomms11618 CrossRef Google Scholar
[125]	Kamali SM, Arbabi E, Arbabi A et al. Highly tunable elastic dielectric metasurface lenses. Laser Photonics Rev 10, 1002–1008 (2016). DOI: 10.1002/lpor.201600144 CrossRef Google Scholar
[126]	Li J, Fan HJ, Ye H et al. Design of multifunctional tunable metasurface assisted by elastic substrate. Nanomaterials 12, 2387 (2022). DOI: 10.3390/nano12142387 CrossRef Google Scholar
[127]	Li WL, He P, Lei DY et al. Super-resolution multicolor fluorescence microscopy enabled by an apochromatic super-oscillatory lens with extended depth-of-focus. Nat Commun 14, 5107 (2023). DOI: 10.1038/s41467-023-40725-9 CrossRef Google Scholar
[128]	Ren YX, He HS, Tang HJ et al. Non-diffracting light wave: fundamentals and biomedical applications. Front Phys 9, 698343 (2021). DOI: 10.3389/fphy.2021.698343 CrossRef Google Scholar
[129]	Bouchal Z. Nondiffracting optical beams: physical properties, experiments, and applications. Czech J Phys 53, 537–578 (2003). DOI: 10.1023/A:1024802801048 CrossRef Google Scholar
[130]	Li DC, Wang XR, Ling JZ et al. Planar efficient metasurface for generation of Bessel beam and super-resolution focusing. Opt Quant Electron 53, 143 (2021). DOI: 10.1007/s11082-021-02765-7 CrossRef Google Scholar
[131]	Lin ZM, Li XW, Zhao RZ et al. High-efficiency Bessel beam array generation by Huygens metasurfaces. Nanophotonics 8, 1079–1085 (2019). DOI: 10.1515/nanoph-2019-0085 CrossRef Google Scholar
[132]	Shi FH, Qiu M, Zhang L et al. Multiplane illumination enabled by Fourier-transform metasurfaces for high-speed light-sheet microscopy. ACS Photonics 5, 1676–1684 (2018). DOI: 10.1021/acsphotonics.7b01457 CrossRef Google Scholar
[133]	Li CS, Guo YH, Chang XZ et al. A metasurface-on-fiber light-sheet generator for biological imaging. Opt Commun 559, 130378 (2024). DOI: 10.1016/j.optcom.2024.130378 CrossRef Google Scholar
[134]	Luo Y, Tseng ML, Vyas S et al. Metasurface‐based abrupt autofocusing beam for biomedical applications. Small Methods 6, 2101228 (2022). DOI: 10.1002/smtd.202101228 CrossRef Google Scholar
[135]	Lu RW, Liang YJ, Meng GH et al. Rapid mesoscale volumetric imaging of neural activity with synaptic resolution. Nat Methods 17, 291–294 (2020). DOI: 10.1038/s41592-020-0760-9 CrossRef Google Scholar
[136]	Wang XW, Nie ZQ, Liang Y et al. Recent advances on optical vortex generation. Nanophotonics 7, 1533–1556 (2018). DOI: 10.1515/nanoph-2018-0072 CrossRef Google Scholar
[137]	Wang S, Li L, Wen S et al. Metalens for accelerated optoelectronic edge detection under ambient illumination. Nano Lett 24, 356–361 (2023). Google Scholar
[138]	Zheludev NI. What diffraction limit. Nat Mater 7, 420–422 (2008). DOI: 10.1038/nmat2163 CrossRef Google Scholar
[139]	Hänninen P. Beyond the diffraction limit. Nature 419, 802 (2002). Google Scholar
[140]	Park SC, Park MK, Kang MG. Super-resolution image reconstruction: a technical overview. IEEE Signal Process Mag 20, 21–36 (2003). DOI: 10.1109/MSP.2003.1203207 CrossRef Google Scholar
[141]	Huang B, Babcock H, Zhuang XW. Breaking the diffraction barrier: super-resolution imaging of cells. Cell 143, 1047–1058 (2010). DOI: 10.1016/j.cell.2010.12.002 CrossRef Google Scholar
[142]	Bliokh KY, Bekshaev AY, Nori F. Extraordinary momentum and spin in evanescent waves. Nat Commun 5, 3300 (2014). DOI: 10.1038/ncomms4300 CrossRef Google Scholar
[143]	Loerke D, Preitz B, Stuhmer W et al. Super-resolution measurements with evanescent-wave fluorescence-excitation using variable beam incidence. J Biomed Opt 5, 23–30 (2000). DOI: 10.1117/1.429964 CrossRef Google Scholar
[144]	Pendry JB. Negative refraction makes a perfect lens. Phys Rev Lett 85, 3966–3969 (2000). DOI: 10.1103/PhysRevLett.85.3966 CrossRef Google Scholar
[145]	Fang N, Lee H, Sun C et al. Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005). DOI: 10.1126/science.1108759 CrossRef Google Scholar
[146]	Lu D, Liu ZW. Hyperlenses and metalenses for far-field super-resolution imaging. Nat Commun 3, 1205 (2012). DOI: 10.1038/ncomms2176 CrossRef Google Scholar
[147]	Kim M, So S, Yao K et al. Deep sub-wavelength nanofocusing of UV-visible light by hyperbolic metamaterials. Sci Rep 6, 38645 (2016). DOI: 10.1038/srep38645 CrossRef Google Scholar
[148]	Jacob Z, Alekseyev LV, Narimanov E. Optical hyperlens: far-field imaging beyond the diffraction limit. Opt Express 14, 8247–8256 (2006). DOI: 10.1364/OE.14.008247 CrossRef Google Scholar
[149]	Liu ZW, Lee H, Xiong Y et al. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007). DOI: 10.1126/science.1137368 CrossRef Google Scholar
[150]	Kastrup L, Blom H, Eggeling C et al. Fluorescence fluctuation spectroscopy in subdiffraction focal volumes. Phys Rev Lett 94, 178104 (2005). DOI: 10.1103/PhysRevLett.94.178104 CrossRef Google Scholar
[151]	Honigmann A, Mueller V, Ta H et al. Scanning STED-FCS reveals spatiotemporal heterogeneity of lipid interaction in the plasma membrane of living cells. Nat Commun 5, 5412 (2014). DOI: 10.1038/ncomms6412 CrossRef Google Scholar
[152]	Barulin A, Kim I. Hyperlens for capturing sub-diffraction nanoscale single molecule dynamics. Opt Express 31, 12162–12174 (2023). DOI: 10.1364/OE.486702 CrossRef Google Scholar
[153]	Wei FF, Ponsetto JL, Liu ZW. Plasmonic structured illumination microscopy. In Liu ZW. Plasmonics and Super-Resolution Imaging 127–163 (Jenny Stanford Publishing, New York, 2017). Google Scholar
[154]	Wei FF, Lu D, Shen H et al. Wide field super-resolution surface imaging through plasmonic structured illumination microscopy. Nano Lett 14, 4634–4639 (2014). DOI: 10.1021/nl501695c CrossRef Google Scholar
[155]	Wei SB, Lei T, Du LP et al. Sub-100nm resolution PSIM by utilizing modified optical vortices with fractional topological charges for precise phase shifting. Opt Express 23, 30143–30148 (2015). DOI: 10.1364/OE.23.030143 CrossRef Google Scholar
[156]	Ponsetto JL, Wei FF, Liu ZW. Localized plasmon assisted structured illumination microscopy for wide-field high-speed dispersion-independent super resolution imaging. Nanoscale 6, 5807–5812 (2014). DOI: 10.1039/C4NR00443D CrossRef Google Scholar
[157]	Ponsetto JL, Bezryadina A, Wei FF et al. Experimental demonstration of localized plasmonic structured illumination microscopy. ACS Nano 11, 5344–5350 (2017). DOI: 10.1021/acsnano.7b01158 CrossRef Google Scholar
[158]	Lee YU, Li SL, Wisna GBM et al. Hyperbolic material enhanced scattering nanoscopy for label-free super-resolution imaging. Nat Commun 13, 6631 (2022). DOI: 10.1038/s41467-022-34553-6 CrossRef Google Scholar
[159]	Rogers ETF, Lindberg J, Roy T et al. A super-oscillatory lens optical microscope for subwavelength imaging. Nat Mater 11, 432–435 (2012). DOI: 10.1038/nmat3280 CrossRef Google Scholar
[160]	Berry MV, Popescu S. Evolution of quantum superoscillations and optical superresolution without evanescent waves. J Phys A: Math Gen 39, 6965–6977 (2006). DOI: 10.1088/0305-4470/39/22/011 CrossRef Google Scholar
[161]	Aharonov Y, Albert DZ, Vaidman L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys Rev Lett 60, 1351–1354 (1988). DOI: 10.1103/PhysRevLett.60.1351 CrossRef Google Scholar
[162]	Huang FM, Zheludev N, Chen YF et al. Focusing of light by a nanohole array. Appl Phys Lett 90, 091119 (2007). DOI: 10.1063/1.2710775 CrossRef Google Scholar
[163]	Zheludev NI, Yuan G. Optical superoscillation technologies beyond the diffraction limit. Nat Rev Phys 4, 16–32 (2022). Google Scholar
[164]	Chen G, Wen ZQ, Qiu CW. Superoscillation: from physics to optical applications. Light Sci Appl 8, 56 (2019). DOI: 10.1038/s41377-019-0163-9 CrossRef Google Scholar
[165]	Qin F, Huang K, Wu JF et al. A supercritical lens optical label‐free microscopy: sub‐diffraction resolution and ultra‐long working distance. Adv Mater 29, 1602721 (2017). DOI: 10.1002/adma.201602721 CrossRef Google Scholar
[166]	Li Z, Zhang T, Wang YQ et al. Achromatic Broadband super‐resolution imaging by super‐oscillatory metasurface. Laser Photonics Rev 12, 1800064 (2018). DOI: 10.1002/lpor.201800064 CrossRef Google Scholar
[167]	Yuan GH, Rogers ETF, Zheludev NI. Achromatic super-oscillatory lenses with sub-wavelength focusing. Light Sci Appl 6, e17036 (2017). DOI: 10.1038/lsa.2017.36 CrossRef Google Scholar
[168]	Rogers ETF, Savo S, Lindberg J et al. Super-oscillatory optical needle. Appl Phys Lett 102, 031108 (2013). DOI: 10.1063/1.4774385 CrossRef Google Scholar
[169]	Roy T, Rogers ETF, Yuan GH et al. Point spread function of the optical needle super-oscillatory lens. Appl Phys Lett 104, 231109 (2014). DOI: 10.1063/1.4882246 CrossRef Google Scholar
[170]	Yuan GH, Rogers ETF, Roy T et al. Planar super-oscillatory lens for sub-diffraction optical needles at violet wavelengths. Sci Rep 4, 6333 (2014). DOI: 10.1038/srep06333 CrossRef Google Scholar
[171]	Diao JS, Yuan WZ, Yu YT et al. Controllable design of super-oscillatory planar lenses for sub-diffraction-limit optical needles. Opt Express 24, 1924–1933 (2016). DOI: 10.1364/OE.24.001924 CrossRef Google Scholar
[172]	Chen G, Wu ZX, Yu AP et al. Planar binary-phase lens for super-oscillatory optical hollow needles. Sci Rep 7, 4697 (2017). DOI: 10.1038/s41598-017-05060-2 CrossRef Google Scholar
[173]	Solli DR, Jalali B. Analog optical computing. Nat Photonics 9, 704–706 (2015). DOI: 10.1038/nphoton.2015.208 CrossRef Google Scholar
[174]	He SS, Wang RS, Luo HL. Computing metasurfaces for all-optical image processing: a brief review. Nanophotonics 11, 1083–1108 (2022). DOI: 10.1515/nanoph-2021-0823 CrossRef Google Scholar
[175]	Selinummi J, Ruusuvuori P, Podolsky I et al. Bright field microscopy as an alternative to whole cell fluorescence in automated analysis of macrophage images. PLoS One 4, e7497 (2009). DOI: 10.1371/journal.pone.0007497 CrossRef Google Scholar
[176]	Marr D, Hildreth E. Theory of edge detection. Proc Roy Soc B Biol Sci 207, 187–217 (1980). Google Scholar
[177]	Canny J. A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell PAMI-8, 679–698 (1986). DOI: 10.1109/TPAMI.1986.4767851 CrossRef Google Scholar
[178]	Maini R, Aggarwal H. Study and comparison of various image edge detection techniques. Int J Image Process 3, 1–12 (2009). DOI: 10.1049/iet-ipr:20080080 CrossRef Google Scholar
[179]	Wang JK, Zhang WH, Qi QQ et al. Gradual edge enhancement in spiral phase contrast imaging with fractional vortex filters. Sci Rep 5, 15826 (2015). DOI: 10.1038/srep15826 CrossRef Google Scholar
[180]	Wei SB, Zhu SW, Yuan XC. Image edge enhancement in optical microscopy with a Bessel-like amplitude modulated spiral phase filter. J Opt 13, 105704 (2011). DOI: 10.1088/2040-8978/13/10/105704 CrossRef Google Scholar
[181]	Yuan S, Xiang D, Liu XM et al. Edge detection based on computational ghost imaging with structured illuminations. Opt Commun 410, 350–355 (2018). DOI: 10.1016/j.optcom.2017.10.016 CrossRef Google Scholar
[182]	Zhou Y, Zheng HY, Kravchenko II et al. Flat optics for image differentiation. Nat Photonics 14, 316–323 (2020). DOI: 10.1038/s41566-020-0591-3 CrossRef Google Scholar
[183]	Chen MK, Wu YF, Feng L et al. Principles, functions, and applications of optical meta‐lens. Adv Opt Mater 9, 2001414 (2021). DOI: 10.1002/adom.202001414 CrossRef Google Scholar
[184]	Abdollahramezani S, Hemmatyar O, Adibi A. Meta-optics for spatial optical analog computing. Nanophotonics 9, 4075–4095 (2020). DOI: 10.1515/nanoph-2020-0285 CrossRef Google Scholar
[185]	Wan L, Pan DP, Yang SF et al. Optical analog computing of spatial differentiation and edge detection with dielectric metasurfaces. Opt Lett 45, 2070–2073 (2020). DOI: 10.1364/OL.386986 CrossRef Google Scholar
[186]	Zhou JX, Qian HL, Zhao JX et al. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl Sci Rev 8, nwaa176 (2021). DOI: 10.1093/nsr/nwaa176 CrossRef Google Scholar
[187]	Guo C, Xiao M, Minkov M et al. Photonic crystal slab Laplace operator for image differentiation. Optica 5, 251–256 (2018). DOI: 10.1364/OPTICA.5.000251 CrossRef Google Scholar
[188]	Kim Y, Lee GY, Sung J et al. Spiral metalens for phase contrast imaging. Adv Funct Mater 32, 2106050 (2022). DOI: 10.1002/adfm.202106050 CrossRef Google Scholar
[189]	Dong HG, Wang FQ, Liang RS et al. Visible-wavelength metalenses for diffraction-limited focusing of double polarization and vortex beams. Opt Mater Express 7, 4029–4037 (2017). DOI: 10.1364/OME.7.004029 CrossRef Google Scholar
[190]	Zhou C, Chen YJ, Li Y et al. Laplace differentiator based on metasurface with toroidal dipole resonance. Adv Funct Mater 34, 2313777 (2024). DOI: 10.1002/adfm.202313777 CrossRef Google Scholar
[191]	Chu CH, Chia YH, Hsu HC et al. Intelligent phase contrast meta-microscope system. Nano Lett 23, 11630–11637 (2023). DOI: 10.1021/acs.nanolett.3c03484 CrossRef Google Scholar
[192]	Overvig A, Alù A. Diffractive nonlocal metasurfaces. Laser Photonics Rev 16, 2100633 (2022). DOI: 10.1002/lpor.202100633 CrossRef Google Scholar
[193]	Shastri K, Monticone F. Nonlocal flat optics. Nat Photonics 17, 36–47 (2023). DOI: 10.1038/s41566-022-01098-5 CrossRef Google Scholar
[194]	Kim M, Lee D, Kim J et al. Nonlocal metasurfaces‐enabled analog light localization for imaging and lithography. Laser Photonics Rev 18, 2300718 (2024). DOI: 10.1002/lpor.202300718 CrossRef Google Scholar
[195]	Li, Shiyu, and Chia Wei Hsu. Thickness bound for nonlocal wide-field-of-view metalenses. Light: Science & Applications 11.1, 338 (2022). DOI: 10.1103/PhysRevLett.121.173004 CrossRef Google Scholar
[196]	Kwon H, Sounas D, Cordaro A et al. Nonlocal metasurfaces for optical signal processing. Phys Rev Lett 121 , 173004 (2018). Google Scholar
[197]	Kwon H, Cordaro A, Sounas D et al. Dual-polarization analog 2D image processing with nonlocal metasurfaces. ACS Photonics 7, 1799–1805 (2020). DOI: 10.1021/acsphotonics.0c00473 CrossRef Google Scholar
[198]	Arnison MR, Larkin KG, Sheppard CJR et al. Linear phase imaging using differential interference contrast microscopy. J Microsc 214, 7–12 (2004). DOI: 10.1111/j.0022-2720.2004.01293.x CrossRef Google Scholar
[199]	Zernike F. How I discovered phase contrast. Science 121, 345–349 (1955). DOI: 10.1126/science.121.3141.345 CrossRef Google Scholar
[200]	Preza C, Snyder DL, Conchello JA. Theoretical development and experimental evaluation of imaging models for differential-interference-contrast microscopy. J Opt Soc Am A 16, 2185–2199 (1999). DOI: 10.1364/JOSAA.16.002185 CrossRef Google Scholar
[201]	Preza C. Rotational-diversity phase estimation from differential-interference-contrast microscopy images. J Opt Soc Am A 17, 415–424 (2000). DOI: 10.1364/JOSAA.17.000415 CrossRef Google Scholar
[202]	Shribak M. Quantitative orientation-independent differential interference contrast microscope with fast switching shear direction and bias modulation. J Opt Soc Am A 30, 769–782 (2013). DOI: 10.1364/JOSAA.30.000769 CrossRef Google Scholar
[203]	Zhao Q, Kang L, Du B et al. Electrically tunable negative permeability metamaterials based on nematic liquid crystals. Appl Phys Lett 90, 011112 (2007). DOI: 10.1063/1.2430485 CrossRef Google Scholar
[204]	Kang B, Woo JH, Choi E et al. Optical switching of near infrared light transmission in metamaterial-liquid crystal cell structure. Opt Express 18, 16492–16498 (2010). DOI: 10.1364/OE.18.016492 CrossRef Google Scholar
[205]	Zhang FL, Zhang WH, Zhao Q et al. Electrically controllable fishnet metamaterial based on nematic liquid crystal. Opt Express 19, 1563–1568 (2011). DOI: 10.1364/OE.19.001563 CrossRef Google Scholar
[206]	Su H, Wang H, Zhao H et al. Liquid-crystal-based electrically tuned electromagnetically induced transparency metasurface switch. Sci Rep 7, 17378 (2017). DOI: 10.1038/s41598-017-17612-7 CrossRef Google Scholar
[207]	Yu P, Li JX, Liu N. Electrically tunable optical metasurfaces for dynamic polarization conversion. Nano Lett 21, 6690–6695 (2021). DOI: 10.1021/acs.nanolett.1c02318 CrossRef Google Scholar
[208]	Badloe T, Kim I, Kim Y et al. Electrically tunable bifocal metalens with diffraction‐limited focusing and imaging at visible wavelengths. Adv Sci 8, 2102646 (2021). DOI: 10.1002/advs.202102646 CrossRef Google Scholar
[209]	Zhou SL, Wu YF, Chen SR et al. Phase change induced active metasurface devices for dynamic wavefront control. J Phys D Appl Phys 53, 204001 (2020). DOI: 10.1088/1361-6463/ab7560 CrossRef Google Scholar
[210]	Ee HS, Agarwal R. Tunable metasurface and flat optical zoom lens on a stretchable substrate. Nano Lett 16, 2818–2823 (2016). DOI: 10.1021/acs.nanolett.6b00618 CrossRef Google Scholar
[211]	Tseng ML, Hsiao HH, Chu CH et al. Metalenses: advances and applications. Adv Opt Mater 6, 1800554 (2018). DOI: 10.1002/adom.201800554 CrossRef Google Scholar
[212]	Dirdal CA, Thrane PCV, Dullo FT et al. MEMS-tunable dielectric metasurface lens using thin-film PZT for large displacements at low voltages. Opt Lett 47, 1049–1052 (2022). DOI: 10.1364/OL.451750 CrossRef Google Scholar
[213]	Han ZY, Colburn S, Majumdar A et al. MEMS-actuated metasurface Alvarez lens. Microsystems 6, 79 (2020). Google Scholar
[214]	Arbabi E, Arbabi A, Kamali SM et al. MEMS-tunable dielectric metasurface lens. Nat Commun 9, 812 (2018). DOI: 10.1038/s41467-018-03155-6 CrossRef Google Scholar
[215]	Luo Y, Chu CH, Vyas S et al. Varifocal metalens for optical sectioning fluorescence microscopy. Nano Lett 21, 5133–5142 (2021). DOI: 10.1021/acs.nanolett.1c01114 CrossRef Google Scholar
[216]	Kim Y, Wu PC, Sokhoyan R et al. Phase modulation with electrically tunable vanadium dioxide phase-change metasurfaces. Nano Lett 19, 3961–3968 (2019). DOI: 10.1021/acs.nanolett.9b01246 CrossRef Google Scholar
[217]	Bai W, Yang P, Huang J et al. Near-infrared tunable metalens based on phase change material Ge₂Sb₂Te₅. Sci Rep 9, 5368 (2019). DOI: 10.1038/s41598-019-41859-x CrossRef Google Scholar
[218]	Afridi A, Gieseler J, Meyer N et al. Ultrathin tunable optomechanical metalens. Nano Lett 23, 2496–2501 (2023). DOI: 10.1021/acs.nanolett.2c04105 CrossRef Google Scholar
[219]	Song YK, Liu WC, Wang XL et al. Multifunctional metasurface lens with tunable focus based on phase transition material. Front Phys 9, 651898 (2021). DOI: 10.3389/fphy.2021.651898 CrossRef Google Scholar
[220]	Crosson B, Ford A, McGregor KM et al. Functional imaging and related techniques: an introduction for rehabilitation researchers. J Rehabil Res Dev 47, vii–xxxiv (2010). Google Scholar
[221]	Tsao J. Ultrafast imaging: principles, pitfalls, solutions, and applications. J Magn Reson Imaging 32, 252–266 (2010). DOI: 10.1002/jmri.22239 CrossRef Google Scholar
[222]	Sezgin E, Schneider F, Galiani S et al. Measuring nanoscale diffusion dynamics in cellular membranes with super-resolution STED–FCS. Nat Protoc 14, 1054–1083 (2019). Google Scholar
[223]	Schermelleh L, Ferrand A, Huser T et al. Super-resolution microscopy demystified. Nat Cell Biol 21, 72–84 (2019). DOI: 10.1038/s41556-018-0251-8 CrossRef Google Scholar
[224]	Kuhlmann AV, Houel J, Brunner D et al. A dark-field microscope for background-free detection of resonance fluorescence from single semiconductor quantum dots operating in a set-and-forget mode. Rev Sci Instrum 84, 073905 (2013). DOI: 10.1063/1.4813879 CrossRef Google Scholar
[225]	Beard P. Biomedical photoacoustic imaging. Interface Focus 1, 602–631 (2011). DOI: 10.1098/rsfs.2011.0028 CrossRef Google Scholar
[226]	Balasubramani V, Kuś A, Tu HY et al. Holographic tomography: techniques and biomedical applications [Invited]. Appl Opt 60, B65–B80 (2021). DOI: 10.1364/AO.416902 CrossRef Google Scholar
[227]	Wang H, Akkin T, Magnain C et al. Polarization sensitive optical coherence microscopy for brain imaging. Opt Lett 41, 2213–2216 (2016). DOI: 10.1364/OL.41.002213 CrossRef Google Scholar
[228]	Baumann B. Polarization sensitive optical coherence tomography: a review of technology and applications. Appl Sci 7, 474 (2017). DOI: 10.3390/app7050474 CrossRef Google Scholar
[229]	Girkin JM, Carvalho MT. The light-sheet microscopy revolution. J Opt 20, 053002 (2018). DOI: 10.1088/2040-8986/aab58a CrossRef Google Scholar
[230]	Chen BC, Legant WR, Wang K et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998 (2014). DOI: 10.1126/science.1257998 CrossRef Google Scholar
[231]	Stelzer EHK, Strobl F, Chang BJ et al. Light sheet fluorescence microscopy. Nat Rev Methods Primers 1, 73 (2021). DOI: 10.1038/s43586-021-00069-4 CrossRef Google Scholar
[232]	Archetti A, Bruzzone M, Tagliabue G et al. Generation of Bessel beam lattices by a single metasurface for neuronal activity recording in zebrafish larva. bioRxiv (2023). https://www.biorxiv.org/content/10.1101/2023.02.12.528189v1 Google Scholar
[233]	Arbabi E, Li JQ, Hutchins RJ et al. Two-photon microscopy with a double-wavelength metasurface objective lens. Nano Lett 18, 4943–4948 (2018). DOI: 10.1021/acs.nanolett.8b01737 CrossRef Google Scholar
[234]	Rynes ML, Surinach DA, Linn S et al. Miniaturized head-mounted microscope for whole-cortex mesoscale imaging in freely behaving mice. Nat Methods 18, 417–425 (2021). DOI: 10.1038/s41592-021-01104-8 CrossRef Google Scholar
[235]	Yao J, Lin R, Chen MK et al. Integrated-resonant metadevices: a review. Adv Photonics 5, 024001 (2023). Google Scholar
[236]	Colburn S, Zhan AL, Majumdar A. Metasurface optics for full-color computational imaging. Sci Adv 4, eaar2114 (2018). DOI: 10.1126/sciadv.aar2114 CrossRef Google Scholar
[237]	Avayu O, Almeida E, Prior Y et al. Composite functional metasurfaces for multispectral achromatic optics. Nat Commun 8, 14992 (2017). DOI: 10.1038/ncomms14992 CrossRef Google Scholar
[238]	Hua X, Wang YJ, Wang SM et al. Ultra-compact snapshot spectral light-field imaging. Nat Commun 13, 2732 (2022). DOI: 10.1038/s41467-022-30439-9 CrossRef Google Scholar
[239]	Tseng E, Colburn S, Whitehead J et al. Neural nano-optics for high-quality thin lens imaging. Nat Commun 12, 6493 (2021). DOI: 10.1038/s41467-021-26443-0 CrossRef Google Scholar
[240]	Chakravarthula P, Sun JP, Li X et al. Thin on-sensor nanophotonic array cameras. ACM Trans Graph 42, 249 (2023). Google Scholar
[241]	Park B, Oh D, Kim J et al. Functional photoacoustic imaging: from nano- and micro- to macro-scale. Nano Converg 10, 29 (2023). DOI: 10.1186/s40580-023-00377-3 CrossRef Google Scholar
[242]	Park B, Lee KM, Park S et al. Deep tissue photoacoustic imaging of nickel(II) dithiolene-containing polymeric nanoparticles in the second near-infrared window. Theranostics 10, 2509–2521 (2020). DOI: 10.7150/thno.39403 CrossRef Google Scholar
[243]	Wang DP, Wang YH, Wang WR et al. Deep tissue photoacoustic computed tomography with a fast and compact laser system. Biomed Opt Express 8, 112–123 (2017). DOI: 10.1364/BOE.8.000112 CrossRef Google Scholar
[244]	Zhao YT, Guo CK, Zhang YQ et al. Ultraviolet metalens for photoacoustic microscopy with an elongated depth of focus. Opt Lett 48, 3435–3438 (2023). DOI: 10.1364/OL.485946 CrossRef Google Scholar
[245]	Li DW, Humayun L, Vienneau E et al. Seeing through the skin: photoacoustic tomography of skin vasculature and beyond. JID innov 1, 100039 (2021). DOI: 10.1016/j.xjidi.2021.100039 CrossRef Google Scholar
[246]	Yao JJ, Wang LV. Sensitivity of photoacoustic microscopy. Photoacoustics 2, 87–101 (2014). DOI: 10.1016/j.pacs.2014.04.002 CrossRef Google Scholar
[247]	Liu WW, Li PC. Photoacoustic imaging of cells in a three-dimensional microenvironment. J Biomed Sci 27, 3 (2020). DOI: 10.1186/s12929-019-0594-x CrossRef Google Scholar
[248]	Liang YZ, Fu WB, Li Q et al. Optical-resolution functional gastrointestinal photoacoustic endoscopy based on optical heterodyne detection of ultrasound. Nat Commun 13, 7604 (2022). DOI: 10.1038/s41467-022-35259-5 CrossRef Google Scholar
[249]	Tearney GJ, Boppart SA, Bouma BE et al. Scanning single-mode fiber optic catheter–endoscope for optical coherence tomography: erratum. Opt Lett 21, 912 (1996). DOI: 10.1364/OL.21.000912 CrossRef Google Scholar
[250]	Tearney GJ, Brezinski ME, Bouma BE et al. In vivo endoscopic optical biopsy with optical coherence tomography. Science 276, 2037–2039 (1997). DOI: 10.1126/science.276.5321.2037 CrossRef Google Scholar
[251]	Hariri LP, Adams DC, Wain JC et al. Endobronchial optical coherence tomography for low-risk microscopic assessment and diagnosis of idiopathic pulmonary fibrosis in vivo. Am J Respir Crit Care Med 197, 949–952 (2018). DOI: 10.1164/rccm.201707-1446LE CrossRef Google Scholar
[252]	Yang JY, Ghimire I, Wu PC et al. Photonic crystal fiber metalens. Nanophotonics 8, 443–449 (2019). DOI: 10.1515/nanoph-2018-0204 CrossRef Google Scholar
[253]	Drexler W. Ultrahigh-resolution optical coherence tomography. J Biomed Opt 9, 47–74 (2004). DOI: 10.1117/1.1629679 CrossRef Google Scholar
[254]	Aumann S, Donner S, Fischer J et al. Optical coherence tomography (OCT): principle and technical realization. In Bille JF. High Resolution Imaging in Microscopy and Ophthalmology: New Frontiers in Biomedical Optics 59–85 (Springer, Cham, 2019). Google Scholar
[255]	Zhao QC, Yuan WH, Qu JQ et al. Optical fiber-integrated metasurfaces: an emerging platform for multiple optical applications. Nanomaterials (Basel) 12 , 793 (2022). Google Scholar
[256]	Pahlevaninezhad M, Huang YW, Pahlevani M et al. Metasurface-based bijective illumination collection imaging provides high-resolution tomography in three dimensions. Nat Photonics 16, 203–211 (2022). DOI: 10.1038/s41566-022-00956-6 CrossRef Google Scholar
[257]	Fröch JE, Huang LC, Tanguy QAA et al. Real time full-color imaging in a meta-optical fiber endoscope. eLight 3, 13 (2023). DOI: 10.1186/s43593-023-00044-4 CrossRef Google Scholar
[258]	Hariri LP, Villiger M, Applegate MB et al. Seeing beyond the bronchoscope to increase the diagnostic yield of bronchoscopic biopsy. Am J Respir Crit Care Med 187, 125–129 (2013). DOI: 10.1164/rccm.201208-1483OE CrossRef Google Scholar
[259]	Adams DC, Hariri LP, Miller AJ et al. Birefringence microscopy platform for assessing airway smooth muscle structure and function in vivo. Sci Transl Med 8, 359ra131 (2016). Google Scholar
[260]	Nadkarni SK, Pierce MC, Park BH et al. Measurement of collagen and smooth muscle cell content in atherosclerotic plaques using polarization-sensitive optical coherence tomography. J Am Coll Cardiol 49, 1474–1481 (2007). DOI: 10.1016/j.jacc.2006.11.040 CrossRef Google Scholar
[261]	Chia YH, Liao WH, Vyas S et al. In vivo intelligent fluorescence endo‐microscopy by varifocal meta‐device and deep learning. Adv Sci 11, 2307837 (2024). DOI: 10.1002/advs.202307837 CrossRef Google Scholar
[262]	Chu CH, Vyas S, Luo Y et al. Recent developments in biomedical applications of metasurface optics. APL Photonics 9, 030901 (2024). DOI: 10.1063/5.0190758 CrossRef Google Scholar
[263]	Gupta J, Das P, Bhattacharjee R et al. Enhancing signal-to-noise ratio of clinical 1.5T MRI using metasurface-inspired flexible wraps. Appl Phys A 129, 725 (2023). DOI: 10.1007/s00339-023-06962-x CrossRef Google Scholar
[264]	Brown MA, Semelka RC. MRI: Basic Principles and Applications (John Wiley & Sons, 2011). Google Scholar
[265]	Plewes DB, Kucharczyk W. Physics of MRI: a primer. J Magn Reson Imaging 35, 1038–1054 (2012). DOI: 10.1002/jmri.23642 CrossRef Google Scholar
[266]	Van Reeth E, Tham IWK, Tan CH et al. Super‐resolution in magnetic resonance imaging: a review. Concepts Magn Reson Part A 40, 306–325 (2012). Google Scholar
[267]	Voormolen EH, Diederen SJH, Woerdeman P et al. Implications of extracranial distortion in ultra-high-field magnetic resonance imaging for image-guided cranial neurosurgery. World Neurosurg 126, e250–e258 (2019). DOI: 10.1016/j.wneu.2019.02.028 CrossRef Google Scholar
[268]	Li ZP, Tian X, Qiu CW et al. Metasurfaces for bioelectronics and healthcare. Nat Electron 4, 382–391 (2021). DOI: 10.1038/s41928-021-00589-7 CrossRef Google Scholar
[269]	Slobozhanyuk AP, Poddubny AN, Raaijmakers AJE et al. Enhancement of magnetic resonance imaging with metasurfaces. Adv Mater 28, 1832–1838 (2016). DOI: 10.1002/adma.201504270 CrossRef Google Scholar
[270]	Stoja E, Konstandin S, Philipp D et al. Improving magnetic resonance imaging with smart and thin metasurfaces. Sci Rep 11, 16179 (2021). DOI: 10.1038/s41598-021-95420-w CrossRef Google Scholar
[271]	Kretov EI, Shchelokova AV, Slobozhanyuk AP. Impact of wire metasurface eigenmode on the sensitivity enhancement of MRI system. Appl Phys Lett 112, 033501 (2018). DOI: 10.1063/1.5013319 CrossRef Google Scholar
[272]	Zhao XG, Duan GW, Wu K et al. Intelligent metamaterials based on nonlinearity for magnetic resonance imaging. Adv Mater 31, 1905461 (2019). DOI: 10.1002/adma.201905461 CrossRef Google Scholar
[273]	Corneanu CA, Simón MO, Cohn JF et al. Survey on RGB, 3D, thermal, and multimodal approaches for facial expression recognition: History, trends, and affect-related applications. IEEE Trans Pattern Anal 38, 1548–1568 (2016). DOI: 10.1109/TPAMI.2016.2515606 CrossRef Google Scholar
[274]	Colburn S, Majumdar A. Single-shot three-dimensional imaging with a metasurface depth camera. arXiv preprint arXiv: 1910.12111 (2019). https://arxiv.org/abs/1910.12111 Google Scholar
[275]	Tsalakanidou F, Malassiotis S. Real-time 2D+ 3D facial action and expression recognition. Pattern Recognit 43, 1763–1775 (2010). DOI: 10.1016/j.patcog.2009.12.009 CrossRef Google Scholar
[276]	Sun LF, Wang ZR, Jiang JB et al. In-sensor reservoir computing for language learning via two-dimensional memristors. Sci Adv 7, eabg1455 (2021). DOI: 10.1126/sciadv.abg1455 CrossRef Google Scholar
[277]	Kwon JM, Yang SP, Jeong KH. Stereoscopic facial imaging for pain assessment using rotational offset microlens arrays based structured illumination. Micro Nano Syst Lett 9, 11 (2021). DOI: 10.1186/s40486-021-00139-y CrossRef Google Scholar
[278]	Imaoka H, Hashimoto H, Takahashi K et al. The future of biometrics technology: from face recognition to related applications. APSIPA Trans Signal Inf Process 10, e9 (2021). Google Scholar
[279]	Woodward Jr JD, Horn C, Gatune J et al. Biometrics: A Look at Facial Recognition (RAND, Santa Monica, 2003). Google Scholar
[280]	Du MY. Mobile payment recognition technology based on face detection algorithm. Concurr Comput Pract Exper 30, e4655 (2018). DOI: 10.1002/cpe.4655 CrossRef Google Scholar
[281]	Li ZL, Dai Q, Mehmood MQ et al. Full-space cloud of random points with a scrambling metasurface. Light Sci Appl 7, 63 (2018). DOI: 10.1038/s41377-018-0064-3 CrossRef Google Scholar
[282]	Xie YY, Ni PN, Wang QH et al. Metasurface-integrated vertical cavity surface-emitting lasers for programmable directional lasing emissions. Nat Nanotechnol 15, 125–130 (2020). DOI: 10.1038/s41565-019-0611-y CrossRef Google Scholar
[283]	Hu T, Zhong QZ, Li NX et al. CMOS-compatible a-Si metalenses on a 12-inch glass wafer for fingerprint imaging. Nanophotonics 9, 823–830 (2020). DOI: 10.1515/nanoph-2019-0470 CrossRef Google Scholar
[284]	Grew N. NOTES of the WEEK. Google Scholar
[285]	Galbally J, Haraksim R, Beslay L. A study of age and ageing in fingerprint biometrics. IEEE Trans Inf Foren Sec 14, 1351–1365 (2019). DOI: 10.1109/TIFS.2018.2878160 CrossRef Google Scholar
[286]	Yager N, Amin A. Fingerprint classification: a review. Pattern Anal Appl 7, 77–93 (2004). DOI: 10.1007/s10044-004-0204-7 CrossRef Google Scholar
[287]	Jain AK, Cao K, Arora SS. Recognizing infants and toddlers using fingerprints: Increasing the vaccination coverage. In Proceedings of IEEE International Joint Conference on Biometrics 1–8 (IEEE, 2014); http://doi.org/10.1109/BTAS.2014.6996252. Google Scholar
[288]	Lee HC, Gaensslen RE. Advances in Fingerprint Technology 2nd ed (CRC Press, Boca Raton, 2001). Google Scholar
[289]	Yang WC, Wang S, Hu JK et al. Security and accuracy of fingerprint-based biometrics: a review. Symmetry 11, 141 (2019). DOI: 10.3390/sym11020141 CrossRef Google Scholar
[290]	Uhl A, Wild P. Comparing verification performance of kids and adults for fingerprint, palmprint, hand-geometry and digitprint biometrics. In Proceedings of the 2009 IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems 1–6 (IEEE, 2009); http://doi.org/10.1109/BTAS.2009.5339069. Google Scholar
[291]	Oh DK, Lee T, Ko B et al. Nanoimprint lithography for high-throughput fabrication of metasurfaces. Front Optoelectron 14, 229–251 (2021). DOI: 10.1007/s12200-021-1121-8 CrossRef Google Scholar

Links

On-chip metasurfaces unlock efficient vector terahertz beams

Jitao Ji, Tao Li, Shining Zhu

Opto-Electronic Advances, DOI: 10.29026/oea.2025.250158
Phase reconstruction via metasurface-integrated quantum analog operation

Qiuying Li, Minggui Liang, Shuoqing Liu, Jiawei Liu, Shizhen Chen, Shuangchun Wen, Hailu Luo

Opto-Electronic Advances, DOI: 10.29026/oea.2025.240239
Focus control of wide-angle metalens based on digitally encoded metasurface

Yi Chen, Simeng Zhang, Ying Tian, Chenxia Li, Wenlong Huang, Yixin Liu, Yongxing Jin, Bo Fang, Zhi Hong, Xufeng Jing

Opto-Electronic Advances, DOI: 10.29026/oea.2024.240095
Advancing nonlinear nanophotonics: harnessing membrane metasurfaces for third-harmonic generation and imaging

Mingbo Pu, Xiangang Luo

Opto-Electronic Advances, DOI: 10.29026/oea.2023.230153
Planar peristrophic multiplexing metasurfaces

Jia Chen, Dapeng Wang, Guangyuan Si, Siew Lang Teo, Qian Wang, Jiao Lin

Opto-Electronic Advances, DOI: 10.29026/oea.2023.220141
Crosstalk-free achromatic full Stokes imaging polarimetry metasurface enabled by polarization-dependent phase optimization

Yaxin Zhang, Mingbo Pu, Jinjin Jin, Xinjian Lu, Yinghui Guo, Jixiang Cai, Fei Zhang, Yingli Ha, Qiong He, Mingfeng Xu, Xiong Li, Xiaoliang Ma, Xiangang Luo

Opto-Electronic Advances, DOI: 10.29026/oea.2022.220058
Photoluminescence control by hyperbolic metamaterials and metasurfaces: a review

Leonid Yu. Beliaev, Osamu Takayama, Pavel N. Melentiev, Andrei V. Lavrinenko

Opto-Electronic Advances, DOI: 10.29026/oea.2021.210031
Ultra-high extinction-ratio light modulation by electrically tunable metasurface using dual epsilon-near-zero resonances

Arash Nemati, Qian Wang, Norman Soo Seng Ang, Weide Wang, Minghui Hong, Jinghua Teng

Opto-Electronic Advances, DOI: 10.29026/oea.2021.200088
Polarization multiplexing for double images display

Jinying Guo, Teng Wang, Baogang Quan, Huan Zhao, Changzhi Gu, Junjie Li, Xinke Wang, Guohai Situ, Yan Zhang

Opto-Electronic Advances, DOI: 10.29026/oea.2019.180029
Tunable and reconfigurable metasurfaces and metadevices

Arash Nemati, Qian Wang, Minghui Hong, Jinghua Teng

Opto-Electronic Advances, DOI: 10.29026/oea.2018.180009

Advanced biological imaging techniques based on metasurfaces

Abstract

Keywords

Introduction

Principle of electromagnetic phase modulation

Propagation phase

Geometric phase

Optimization of unit cell period

Dispersion modulation

Materials for metasurface

Plasmonic material

Dielectric material

Tunable material

Applications

Metasurfaces for cell imaging applications

Super-resolution imaging

Edge-detection metasurface

Tunable metasurfaces

Metasurfaces for tissue and animal imaging applications

Fluorescent microscopy

Photoacoustic microscopy (PAM)

Metasurfaces for human applications

Endoscopic imaging

Magnetic resonance imaging (MRI)

Devices for facial recognition

Devices for fingerprint recognition

Conclusions and future perspectives

Acknowledgements

Competing interests

References

Cited by

Periodical cited type(19)

Other cited types(0)

Author Information

Yongjae Jo On this SiteOn Google Scholar

Hyemi Park On this SiteOn Google Scholar

Hyeyoung Yoon On this SiteOn Google Scholar

Corresponding author: Inki Kim, inki.kim@skku.edu On this SiteOn Google Scholar

Author contributions

Copyright

About this Article

Cite this Article

Article History

Article Metrics

Related Articles

Links

Related Articles

Catalog

Corresponding author: Inki Kim, inki.kim@skku.edu

Manuscript Submission

More Content

Legal & Privacy

Export File

Citation

Format

Content

WeChat Qrcode

Yongjae Jo On this Site On Google Scholar

Hyemi Park On this Site On Google Scholar

Hyeyoung Yoon On this Site On Google Scholar

Corresponding author: Inki Kim, inki.kim@skku.edu On this Site On Google Scholar