Research on dynamic variance threshold algorithm based on distributed fiber vibration sensor system

Zhang Bozhi; Liu Ke; Liu Kun; Jiang Junfeng; Zhang Man; Liu Tiegen

doi:10.12086/oee.2023.220205

Abstract

In order to solve the problems of weak positioning accuracy, low sensitivity, and slow response speed of the distributed fiber vibration sensor system, a dynamic variance threshold algorithm based on the phase-sensitive photosensitive time domain reflection is proposed. The signal preprocessed by the band-pass filter is processed by variance processing, Gaussian blur, threshold peak seeking, and accurate center of gravity. The problem of long response time caused by the attenuation of Rayleigh scattering signal and the large amount of computation in the long-distance DVS detection is solved. The parallel programming technology is used to improve the operation speed by 184%, so as to quickly and accurately determine the location of the disturbance. The difference between the man-made disturbance and the noise on a 39 km long optical fiber is experimentally studied, and the influence of the noise is eliminated by the dynamic variance algorithm. The response time of the system is 1 second, the spatial resolution is 20 meters, and the positioning error is less than 0.1%.

Keywords

FullText(HTML)

1. 引　言

随着发电站、管线^[2-3]、桥梁以及隧道^[4-5]等技术水平的不断提升，其主要基础设施中的安全问题日益受到人们的关注。传感技术挖掘与发展，是实现感知物理量变化的一种有效途径。美国TAMU在1993年利用外部振动采用背向瑞利散射光的相位调制进行振动分析^[6]。基于超窄线宽激光光源的${\text{ϕ}} $-OTDR技术第一次走向世人。中国科学院上海光机所梁可桢等人于2012年提出了一种新型的数字相干监测和维纳滤波技术的振动监测技术，传感距离达到了3.5 km，检测到振动频率为200 Hz的正弦信号^[7]。Hugo F. Martins等人于2013年提出了一种${\text{ϕ}}$-OTDR系统，用于高精度的超声波测定^[8]。天津大学孙振世在2016年进行了分布式光纤振动传感器对压力水管泄漏检测的研究^[9]。安徽大学俞本立教授在2017年采用统计计算方法，有效地抑制了误差。武汉理工大学李信宇等人于2019年提出了一种基于弱光栅阵列增强的${\text{ϕ}}$-OTDR传感系统，为高灵敏度的分布式振动测量提供了一种方法^[10]。吴慧娟等人于2021年介绍了DVS/DAS信噪分离、基于机器学习模型的多维信号的检测和识别算法^[11]。

在长距离DVS应用中，检测信号的衰减主要是因为在长距离传输时瑞利散射发生减弱^[12]，而且地面生活场景的复杂及未知地埋条件下导致实际误报率偏高问题，使得DVS的长距离检测算法还不能达到实际应用的要求，如高灵敏度以及低误报率等^[13]。DVS长距离检测算法在边界安防、管道泄漏、长距离光纤传输安全等应用中具有重大意义。

分布式光纤振动传感系统(Distributed vibration system, DVS)是通过光纤作为传感敏感元件来感知振动。利用光时域反射测量技术(optical time domain reflectometer, OTDR)实现了对某一或多个振动点在同一时间内的感知和空间定位实时准确测量^[1]。其在长距离、全方位、多点非法入侵、结构损坏等振动相关事件的应用，优于常规振动检测系统，其优势是不受电磁干扰、探测距离长、定位精度高、可实现连续多点分布式测量。目前，以瑞利散射、拉曼散射和布里渊散射为基础，构成了分布式光纤传感系统的重要光学理论。在光纤传输过程中，散射的主要成分是瑞利散射，它的散射强度更高。激光信号经脉冲调制后，在光纤全程上各个点到达探测器的背向散射光的时间也各不相同，光强度也各不相同，通过探测器的背向瑞利散射光强度可以用来表示光纤全程的干扰。

因此，本文根据方差分析能在一维信号中迅速、高效地检测振动特征，提出了一种动态方差阈值算法，并使用了能提高系统响应速度的并行编程技术。

2. 理论推导

2.1 ϕ-OTDR原理分析

所以采集到的信号是光纤沿线各个位置的背向瑞利散射光相位随着位置变化而变化的曲线。

式中：t为光信号从发射到接收所用的时间，n为光纤的纤芯折射率，S为传输距离，c为光在真空中的传播速度^[14]。由式(1)可知，瑞利散射光返回的速度越快，距离光源越近，返回时间和距离呈线性关系。采集卡接收到信号的时间顺序即为信号的位置信息。

t = 2 n S / c,

Δ φ = \frac{2 π}{λ} (l Δ n + n ε l),

光纤的折射率会由于在该位置上的传感光纤受外界扰动的影响而改变，从而引起光在相应位置上相位的改变，其相位变化如式(2)所示：

瑞利散射是一种波长与入射光相同的弹性散射。瑞丽背向散射的传输距离与时间的关系式如式(1)所示：

式中：λ为光的中心波长，l为光纤长度，ε为光纤的应变张量。相位的改变会影响该位置电场的变化，最终反映出光的相位变化^[15]。采集卡接收到的电场变化即为信号的相位变化。

2.2 动态方差阈值算法

Figure 1. Full-Size Img PowerPoint

Algorithm flow chart

Y = [\begin{matrix} y_{1} \\ ⋮ \\ y_{i} \end{matrix}] .

X = [\begin{array}{ccc} x_{11} & \dots & x_{1, j} \\ ⋮ & ⋱ & ⋮ \\ x_{i, 1} & \dots & x_{i, j} \end{array}],

Z = [\begin{matrix} z_{1} \\ ⋮ \\ z_{i} \end{matrix}] .

经过方差处理后，对矩阵Y进行高斯模糊处理：

在对采集的数据进行预处理并将所得曲线平滑处理后，若想确定扰动位置则需要对曲线进行阈值寻峰。在短距离的DVS系统中，可以取固定阈值来得到振动峰的起始点和结束点，并求出该振动峰的重心位置，从而得到震动的精确位置。在长距离的DVS系统寻峰算法中，随着距离增加，光信号会衰减，信号的强度也会减弱。这种衰减有些固定的趋势：在十公里内衰减十分明显，十公里后衰减的速度逐渐放慢。因为这一趋势的变化，我们的算法也会受到影响。当我们完成第二步方差加模糊算法之后，就可以得到一个很明显的波形，通过阈值寻峰很容易得到波峰的具体位置。这种算法在短距离(5 km以内)没有明显的问题，但在长距离的情况下，因为原始信号值随着距离的增加而逐渐衰减，初始端电压和末端电压相差很多，导致我们前面得到的结果波形高度也会差很多^[17]，这种情况下如果继续使用固定的阈值，显然是不可取的。所以我们使用一段距离的平均值作为动态阈值，这段距离的宽度选取需要谨慎，通过对比10 m、500 m、1 km、5 km的距离宽度发现，距离宽度太小容易被扰动位置干扰，太长则会准确度不足。所以我们采用1 km作为平均值的距离宽度，该宽度生成的阈值能保证低漏报率及低错报率。

将矩阵Z绘制成曲线，将波形进行平滑连续的优化，有利于后续的阈值寻峰算法。若不对曲线进行平滑连续的优化则会造成存在反复穿越阈值的现象，从而产生误报。

从而将每个点采集到的一维信号转换成一个具体的数值，并且这个数值能够区分扰动/非扰动。如果是平静的位置，那么该位置的数据的方差相对于相邻位置的方差变化较小；如果是扰动的位置，那么该位置的数据的方差相对于相邻位置的方差变化较大。

其中：i为采样的位置数，j为每秒钟采样的帧数。对矩阵X逐行进行方差处理：

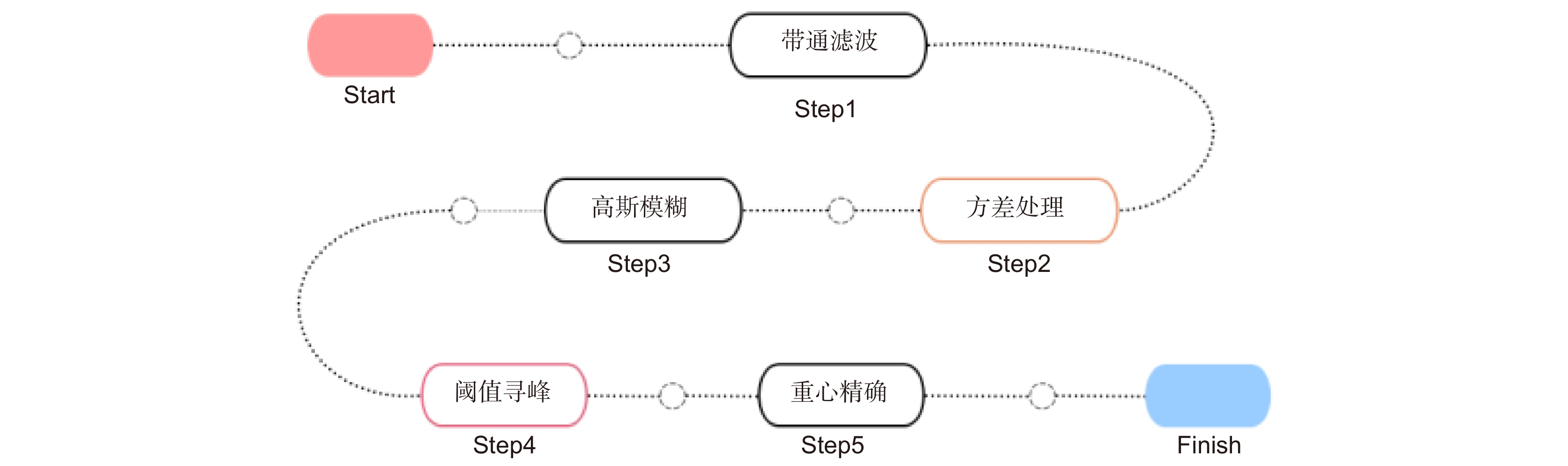
图1为动态方差阈值算法流程图，首先将采集的信号通过带通滤波器进行降噪预处理，以便对扰动信号更精确地辨识。每个位置采集的全部数据可以用矩阵X来表示：

z_{i} = \frac{y_{i - m} \cdot w_{i - m} + y_{i - m + 1} \cdot w_{i - m + 1} + \dots + y_{i} z_{i} + \dots y_{i + m} w_{i + m}}{2 m + 1},

y_{i} = \frac{1}{j} [{(x_{i, 1} - {\overset{―}{x}}_{i})}^{2} + {(x_{i, 2} - \overset{―}{x_{i}})}^{2} + \dots + {(x_{i, j} - \overset{―}{x_{i}})}^{2}] .

得到了矩阵Y：

式中：m为高斯模糊的宽度，w为高斯分布的系数^[16]。得到了矩阵Z:

2.2.1 带通滤波

带通滤波器可以有效地抑制输入信号在一定的频率范围外的信号成分，避免了特定范围外的波动。带通滤波器会使信号频率成分在一定的频率范围内下降，只允许一定频率范围内的信号成分通过^[12]。带通滤波器分为：FIR(有限冲激响应滤波器)，IIR(无限冲激响应滤波器)。FIR滤波器在保证幅度特性满足技术要求的同时，有做到严格的线性相位特性，故在本文采用了FIR滤波器。带通滤波器具有天然去噪的优势并且在DVS系统中的速度也很快。由于光时域反射信号具有其特定频率范围，且无论是光路还是电路的噪声都会对解调有影响，所以我们将FIR滤波器应用在DVS系统中从而降低噪声干扰、提高信噪比。

2.2.2 方差分析

方差是在统计学上反映出随机变量离散程度的物理量。在概率论中用方差对随机变量与其数学期望(即均值)之间的偏离程度进行度量。统计中的方差(样本方差)为各样本值与全部样本值平均数之差的平方值的平均数^[18]。在很多实际应用中，研究数据的偏差程度，也就是方差，是非常有意义的。

方差分析是一种显著性试验，用于两个或两个以上的均数差异。研究得出的数据因各种因素而呈现波动状。引起波动的原因分为两类，一类是不可控的随机因素，另一类是实验中主动施加的影响因素。在DVS系统中，环境噪声是一个不可控的随机因素，而扰动是一个影响因素，它是主动施加的。

2.2.3 高斯模糊

高斯模糊又称高斯平滑，它通常用于降低影像杂讯，减少细节层次，广泛应用于影像处理领域。通过高斯模糊技术处理后的影像，其视觉效果与在一般灯光阴影下使用毛玻璃作为镜头观察图像的效果相近^[19]。高斯平滑也常用于计算技术视觉算法中的预处理阶段，以增强不同比例大小下的图像效果(参见尺度空间表示以及尺度空间实现)。图像的高斯模糊过程，数学上可以理解为图像与正态分布做卷积。影像模糊做卷积搭配圆形边框，会产生更精准的焦外影像效果。高斯模糊可以看作图像低通滤波器，因为高斯函数的傅里叶变换是另一个高斯函数。在DVS算法数据处理中可以将采集到的波形进行平滑连续的优化，从而有利于后续的阈值寻峰算法。

3. 实验结果

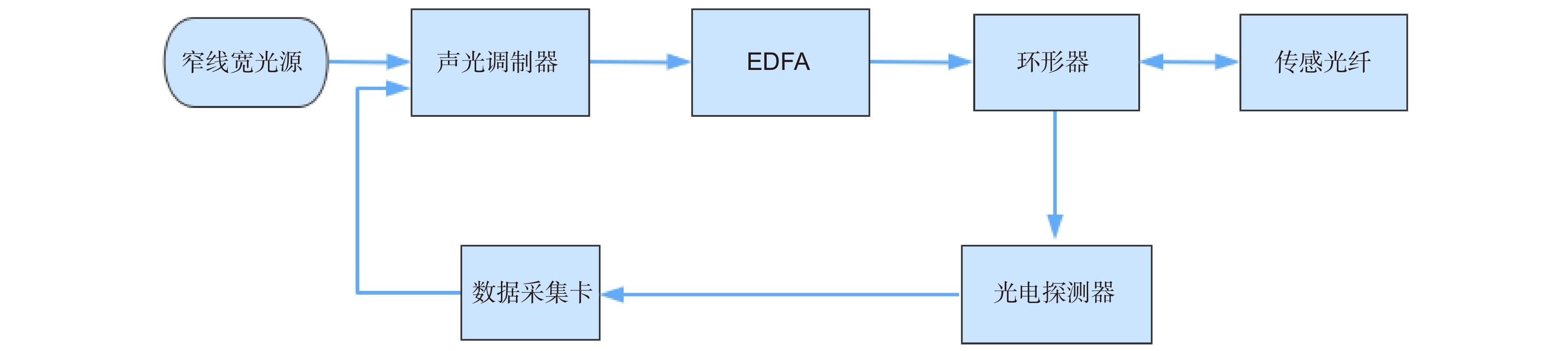
如图2所示，文中所做的实验硬件系统，采用声光调制器(AOM)实现了对超窄线宽激光器发射的脉冲调制，生成了一个连续相干脉冲光信号。利用环形器将EDFA放大后的光脉冲信号传输到传感光纤中。并且通过环形器，将脉冲光信号在传感光纤中所产生的背向瑞利散射信号输入到光电探测器中，由此进入数据采集卡处理信号^[20]。由于要进行长距离振动检测，我们结合了前向拉曼放大，使得传感距离长达39 km。其中，数据采集卡的脉冲周期为1 kHz，脉冲宽度为200 ns，采样率为100 MHz。拉曼放大器功率为27 dBm。

Figure 2. Full-Size Img PowerPoint

Structural diagram

3.1 噪声分析

4) 光路引起的噪声。如光缆熔接头、法兰接头处，不干净的接头面等引起，此类噪声较容易处理。

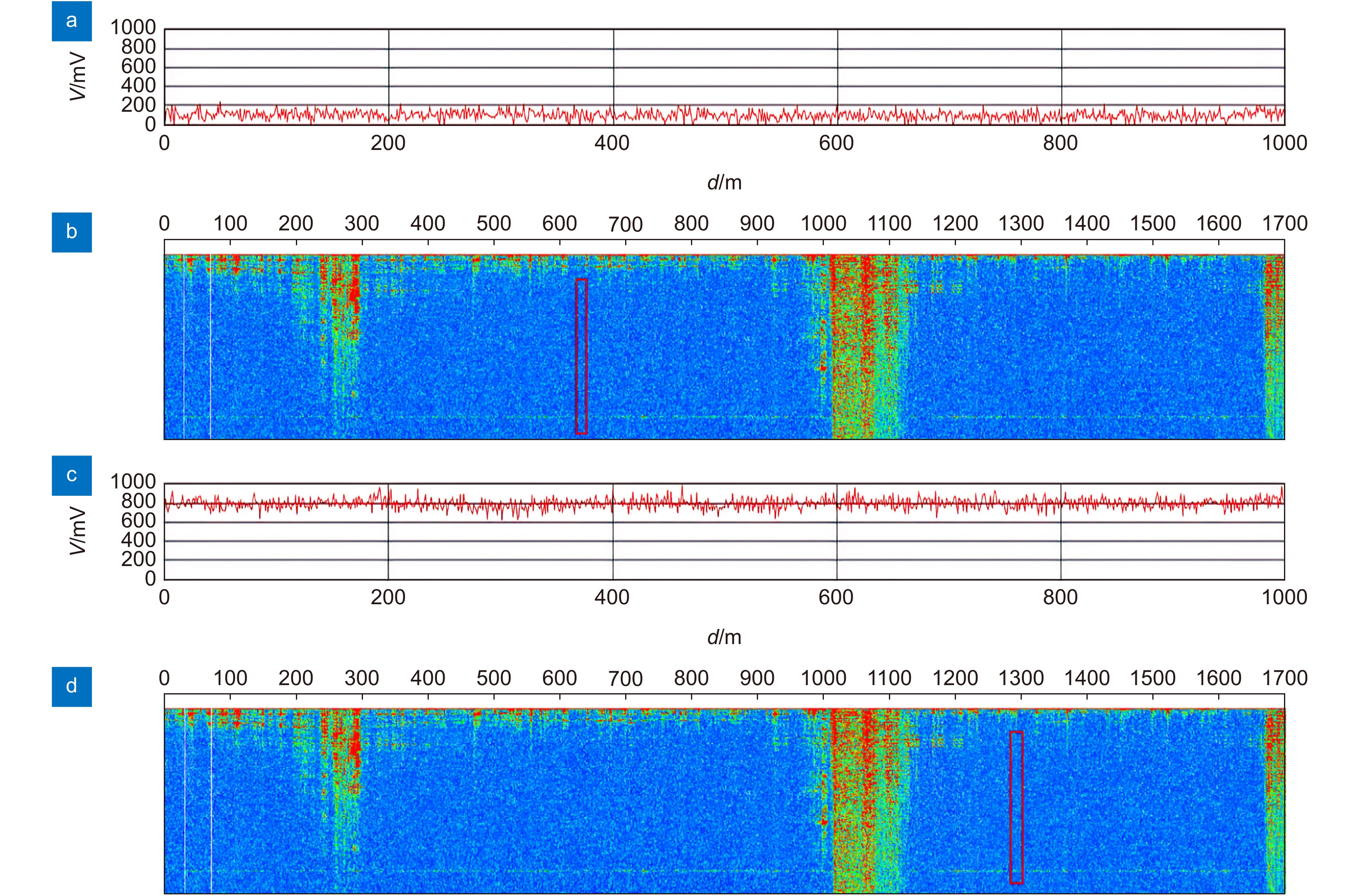
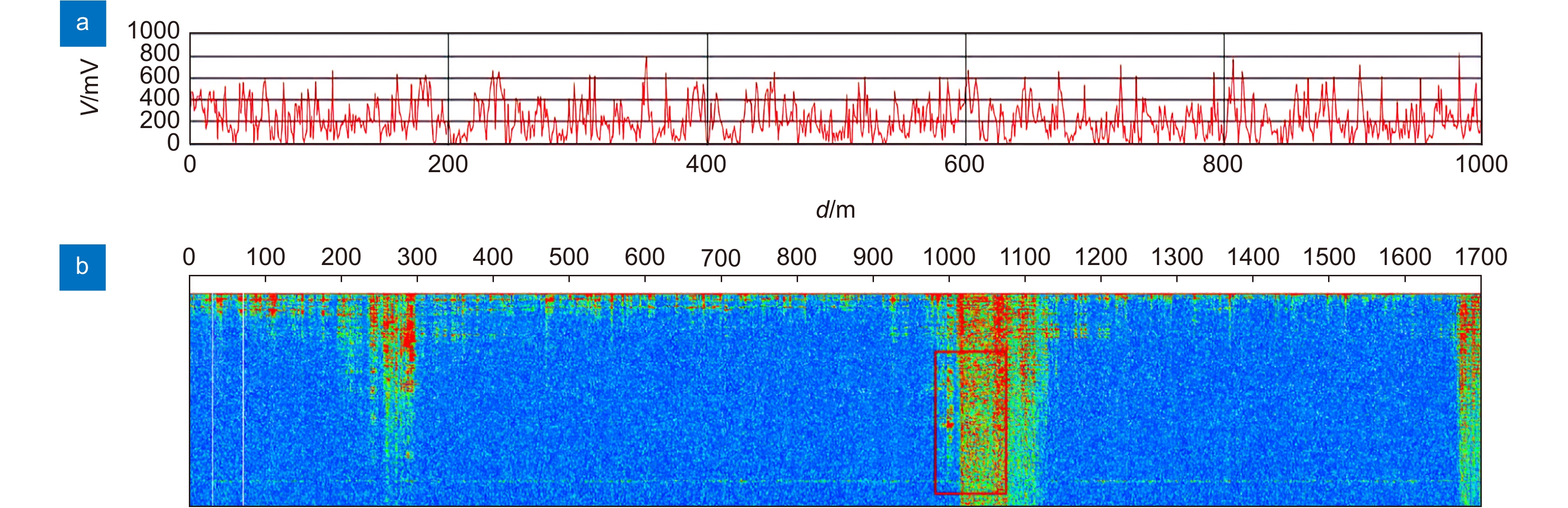
如图3所示，平静位置的信号无论高低，都具有较小振幅的特点，振幅基本在200 mV左右，变化较小。

平静位置的信号特点：较为平稳，1000个点的振幅分布在200 mV的阈值范围内。整体曲线相当平滑。大部分位置具有较低的能量，电压值集中在200 mV以下，如图3(a)、3(b)；小部分电压值由于实验光缆铺设存在多种干扰(空调室外机，光缆悬挂)，存在600 mV~1000 mV不等的较高电压，如图3(c)、3(d)。而扰动位置电压值振幅较大，如图4所示，信号不平稳，波动大，振幅最高能达到1000 mV，整体曲线呈锯齿状。根据采集的各种噪声频率范围，本次实验的FIR带通滤波器频率范围设置为40 Hz～500 Hz，我们可以通过振幅大小来区分扰动和平静位置。

Figure 3. Signal characteristics of two quiet positions and their corresponding positions in the spectrum (abscissa is position/m, ordinate is frequency/Hz)

Figure 3. Full-Size Img PowerPoint

Signal characteristics of two quiet positions and their corresponding positions in the spectrum (abscissa is position/m, ordinate is frequency/Hz)

对分析不利的信号均可称作噪声。通过实际检测，发现DVS噪声大致分为以下几类：

3) 电子元器件引起的噪声。比如采集卡内部的噪声，信号线的噪声等。此类噪声一般较弱且容易规避。

1) 偏振引起的噪声。特点表现为偶发性的低频高能量。在光缆悬挂晃动时可能会出现。影响较大，但其集中分布在低频段，所以容易处理。

2) 外界物理噪声。比如DVS传感光缆附近的震动装置。常见的有空调机，高压电线上的震动装置，影响较大且不容易避免。即便知道外界震动的固有频率也不容易消除，因为当外界的固定频率震动传递到光缆时，引起的光信号的震动不是固有频率^[21]。

Figure 4. The data of 1000 frames at the disturbance location and the corresponding position of its spectrum (abscissa is position/m, ordinate is frequency/Hz)

Figure 4. Full-Size Img PowerPoint

The data of 1000 frames at the disturbance location and the corresponding position of its spectrum (abscissa is position/m, ordinate is frequency/Hz)

3.2 平均模糊与高斯模糊比较

在DVS系统中，最后得到的波形往往不是平滑连续的，这不利于后续的寻峰算法。通常采用加权平均模糊算法来解决这个问题^[22]。加权平均的算法十分简单：取目标点前后点的各点平均值与权重的乘积的和来代替这个点的值。权重的取值是这一算法的关键：可以取所有点的权重相同，也就等于多个点平均值。这种做法虽然算法简单、速度快，但是会出现一定程度的失真。因此，本文采用高斯分布的加权平均算法既能平滑曲线又能很好地保留曲线特征。

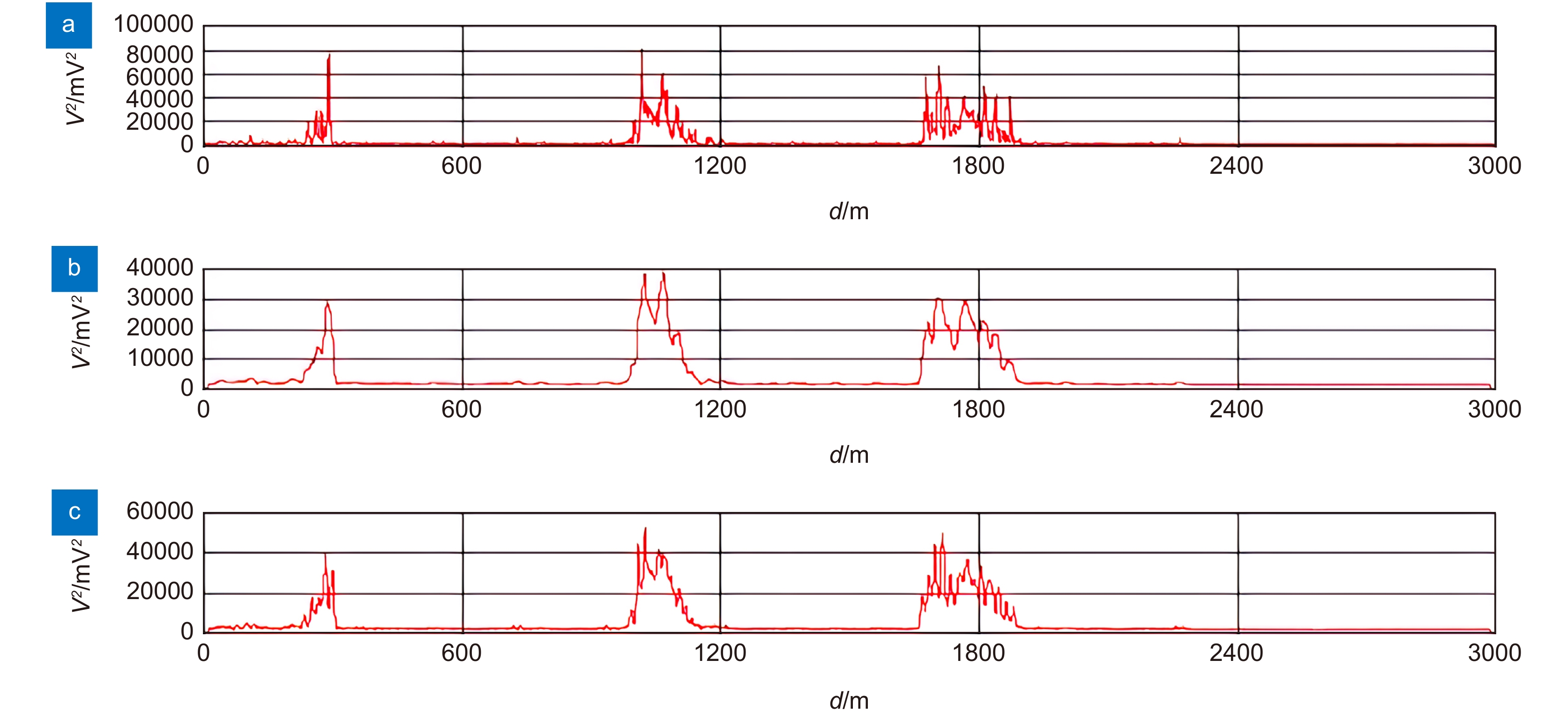
由图5可以看出，高斯模糊在保留原曲线特征的同时将曲线进行平滑，效果优于平均模糊^[23]。若不对方差曲线进行高斯模糊处理，在寻峰算法时对同一位置的扰动识别为多个峰，从而增大误报率。在高斯模糊中，其标准差代表着数据的离散程度，标准差越高生成模版的各个系数相差较小，对图像的平滑效果比较明显。宽度代表着加权平均的范围。当宽度等于六倍标准差时其概率分布为99.8%。本次实验中，我们采用3的标准差，即21的宽度，这样既能保证曲线的平滑效果，又能保留原曲线的特征。

Figure 5. Gaussian blur. (a) Before blurring; (b) Average blurring with a width of 20; (c) Gaussian fuzzy. The standard deviation sigma of Gaussian fuzzy is equal to 3, and the width is 21 points

Figure 5. Full-Size Img PowerPoint

Gaussian blur. (a) Before blurring; (b) Average blurring with a width of 20; (c) Gaussian fuzzy. The standard deviation sigma of Gaussian fuzzy is equal to 3, and the width is 21 points

3.3 使用并行编程技术提高运算速度

在Task的基础上进行封装得到了Parallel，可以同时使主线程(当前线程)+等候线程参与计算。

本系统的数据处理采用多线程模式，而多线程的相当一部分时间是用于线程上下切换。所以在使用多线程时，线程池一般都是搭配使用的。C#中使用线程池技术很简单，关键在于如何设置最大线程数，主要有以下两种类型：

Parallel可以执行多个指令，同时启动多个线程，是一种多线程的操作。主线程(当前线程)也会参与计算—阻塞界面(主线程忙于计算，无暇他顾)是Parallel最直观的特点。

分别使用十组不同的数据进行测算。串行处理平均288 ms，并行处理平均103 ms。串行处理平均CPU占有率为13%，并行处理平均CPU占有率为40%。在对40 km的数据进行处理时，串行处理时长为3.7 s，并行处理仅需1 s。并行处理的速度比串行快了将近三倍。优势很明显。

IO密集型，最大线程数往往要比计算密集型高很多，几十到几百都有可能，具体要搭配IO的速度。C#在新的版本中，提供了简单易用的并行编程APi，Parallel。

计算密集型，一般使用2*CPU核数+2。例如计算机是4核，那么使用10线程效果最佳。

4. 数据分析

第一种方法：将从振动峰初始点到结束点的所有点(包括初始点和结束点)的横纵坐标相乘后累加得到的数值除以二得到x_w，再从起始点x₀开始累加，直到x₀+x₁+x₂+$ \cdots + $x_i 大于x_w，则x_i为重心位置，也即振动的精确位置。

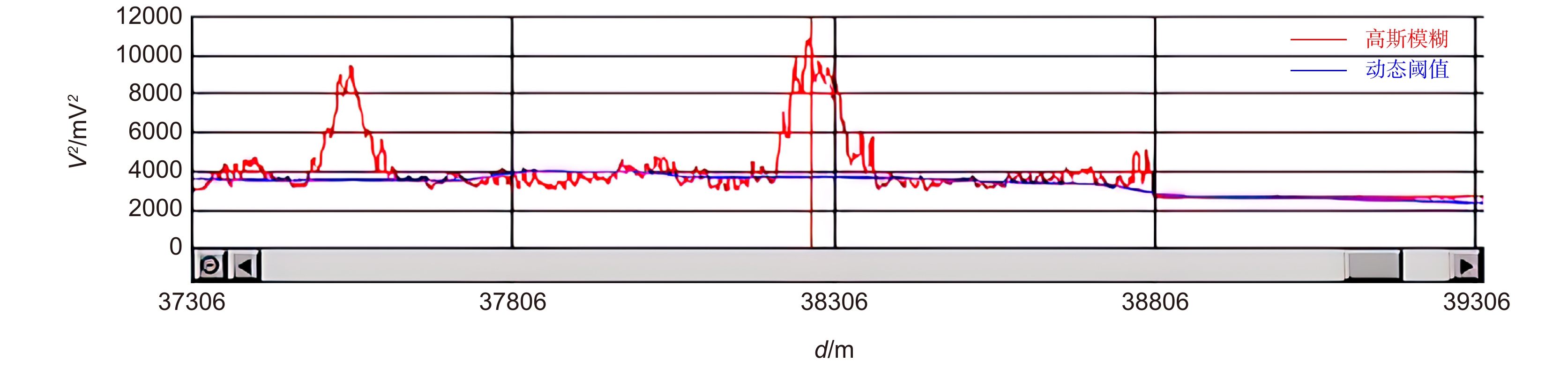
经阈值寻峰算法得到的扰动位置为37556 m和38243 m，误差小于0.1%，漏报率为0，响应时间为1 s。

最后对寻到的两个峰进行重心确定。振动峰重心确定有两种方法：

Figure 7. Full-Size Img PowerPoint

Raw data

W_{1} * L = G * X_{1} .

Figure 6. Full-Size Img PowerPoint

Test site

Figure 9. Full-Size Img PowerPoint

Disturbance prescription difference curve

Figure 8. Full-Size Img PowerPoint

Variance treatment

若重力G已知，则重心位置直接可求，如果不确定，则将杆反向再重复做一遍，可建立一个方程，重心位置即可求。第一种方法的操作数远多于第二种方法，所需时间更多。本文采用第二种方法求得振动的精确位置。

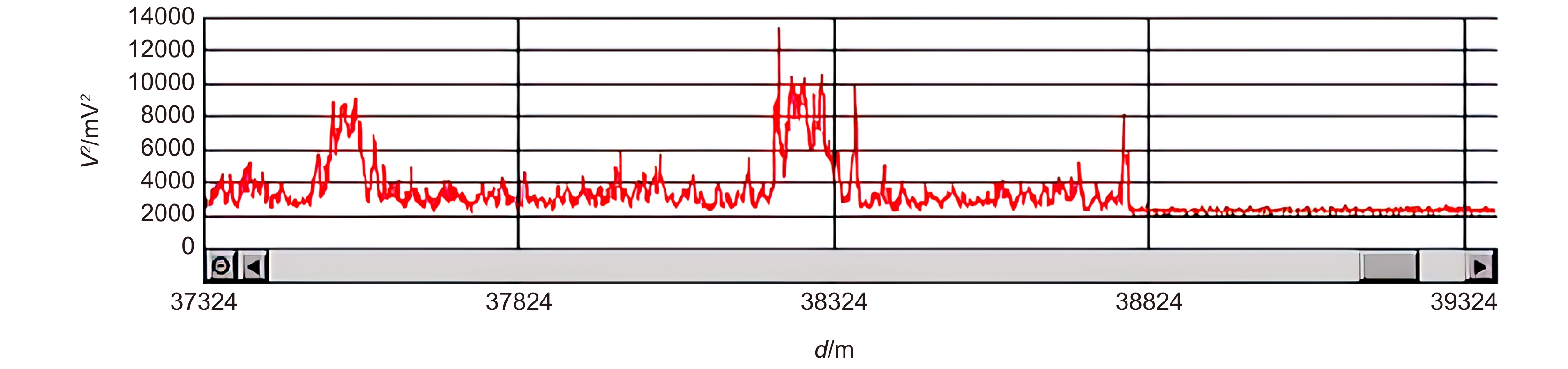
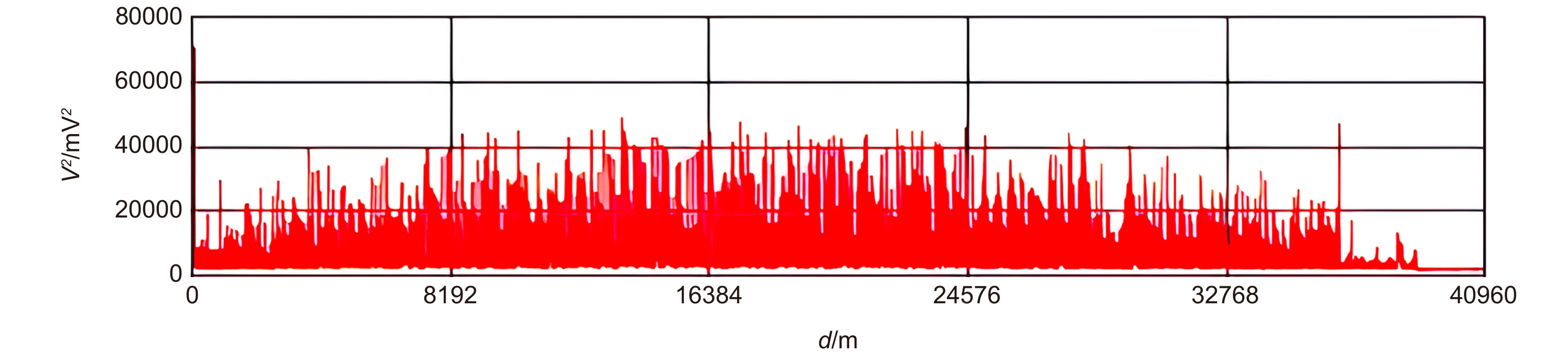
高斯模糊后得到了连续的一维位置与电压的曲线，进行寻峰处理。图8为原始数据经方差处理后的数据曲线，图9为扰动处经方差处理后的数据曲线放大图。在寻峰算法中，如图10所示取每个位置前后500 m，共1001个点的平均值来绘制动态阈值曲线。通过对比噪声与各种人为扰动(晃动、敲击、翻越)的信号特征发现，人为扰动的峰宽度均大于80 m，所以寻峰宽度也设置为80 m，从而区分扰动和噪声。

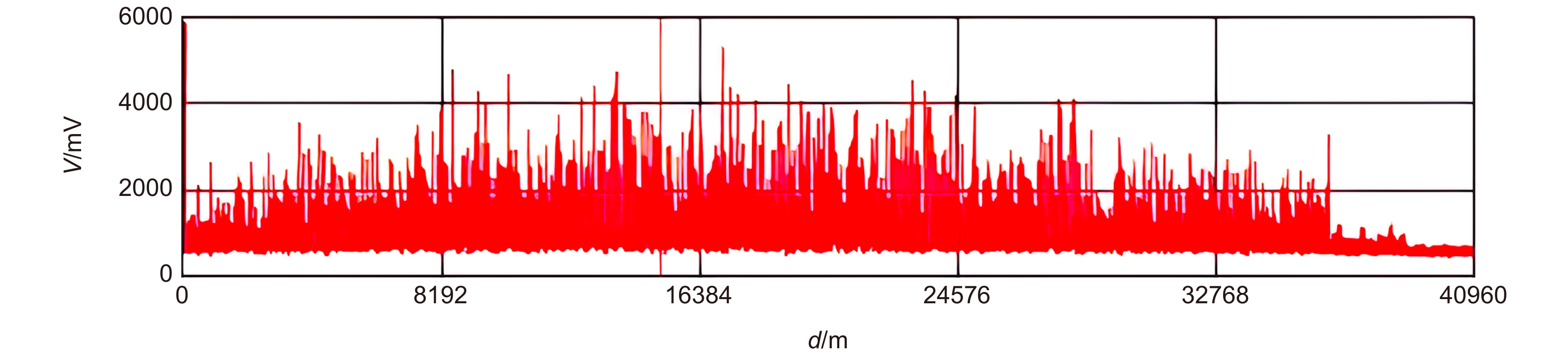
如图6所示，我们在37 km的盘纤后接入3 km的测试光缆进行现场测试，图7为原始数据，共设置了40960个位置，间隔1 m，每个位置采集1000帧数据。在实验过程中，我们主要以最后3 km进行扰动测试，通过晃动、敲打以及翻越的方式进行人为扰动。由原始数据可以看出，在系统中加入拉曼放大器有效减缓了光信号的衰减^[24]。由于前37 km的盘纤更加敏感并且实验环境为自然环境，所以其也处于一定的振动状态。但这种振动与人为的扰动不同，在方差处理后具有相近的能量值，在后续寻峰算法中不会形成扰动峰，从而进行排除，在37550 m和38250 m处进行人为扰动。

Figure 10. Full-Size Img PowerPoint

Peak seeking algorithm

第二种方法：根据力矩求重心位置。将振动峰当成一根质量不均匀的直杆，振动峰上的点的横坐标即为在该直杆上的位置，纵坐标即为该位置点上的重量^[25]。直杆上的重量值分布于位置点上，假定一重杆长度为L，将杆一端支架，用秤称量另一端。设X₁为重心到支承端距离，G是杆的重力，另一端的重力为W₁，则根据力矩平衡有：

5. 结　论

光纤检测相较于传统振动监测方法有着巨大优势，并且分布式光纤振动检测系统在工程应用得到了更加广泛的使用。因此，提高检测系统的精确度和灵敏度就显得尤为重要^[26]。

本文首先在理论上分析了φ-OTDR的原理以及噪声和扰动的信号特征，然后提出了一种基于φ-OTDR的动态方差阈值算法，解决了长距离分布式振动检测算法由于光信号衰减和噪声扰动造成的灵敏度和准确率低的问题。实验数据表明，该算法具有高定位精度及快速响应的优点，并且能对多种扰动进行反应，能广泛地应用在工程实践当中，如管道泄漏、边界安防、建筑健康监测等。

利益冲突

刘铁根是期刊的编委，除此之外，所有作者声明无利益冲突。

References (26)

References

[1]	Juarez J C, Maier E W, Choi K N, et al. Distributed fiber-optic intrusion sensor system[J]. J Lightwave Technol, 2005, 23(6): 2081−2087. DOI: 10.1109/JLT.2005.849924 CrossRef Google Scholar
[2]	Tan D J, Tian X Z, Sun W, et al. An oil and gas pipeline pre-warning system based on Φ-OTDR[J]. Proc SPIE, 2014, 9157: 91578W. DOI: 10.1117/12.2054698 CrossRef Google Scholar
[3]	吴慧娟, 陈忠权, 吕立冬, 等. 基于DOFVS的新型压力输水管道泄漏在线监测方法[J]. 仪器仪表学报, 2017, 38(1): 159−165. DOI: 10.3969/j.issn.0254-3087.2017.01.021 Wu H J, Chen Z Q, Lv L D, et al. Novel pressurized water pipe leak monitoring method based on the distributed optical fiber vibration sensor[J]. Chin J Sci Instrument, 2017, 38(1): 159−165. DOI: 10.3969/j.issn.0254-3087.2017.01.021 CrossRef Google Scholar
[4]	Bao X Y, Zhou D P, Baker C, et al. Recent development in the distributed fiber optic acoustic and ultrasonic detection[J]. J Lightwave Technol, 2017, 35(16): 3256−3267. DOI: 10.1109/JLT.2016.2612060 CrossRef Google Scholar
[5]	Duckworth G L, Ku E M. OptaSense distributed acoustic and seismic sensing using COTS fiber optic cables for infrastructure protection and counter terrorism[J]. Proc SPIE, 2013, 8711: 87110G. DOI: 10.1117/12.2017712 CrossRef Google Scholar
[6]	Taylor H F, Lee C E. Apparatus and method for fiber optic intrusion sensing: 5194847[P]. 1993-03-16. Google Scholar
[7]	梁可桢, 潘政清, 周俊, 等. 一种基于相位敏感光时域反射计的多参量振动传感器[J]. 中国激光, 2012, 39(8): 0805004. DOI: 10.3788/CJL201239.0805004 Liang K Z, Pan Z Q, Zhou J, et al. Multi-parameter vibration detection system based on phase sensitive optical time domain reflectometer[J]. Chin J Lasers, 2012, 39(8): 0805004. DOI: 10.3788/CJL201239.0805004 CrossRef Google Scholar
[8]	Martins H F, martin-Lopez S, Corredera P, et al. High visibility phase-sensitive optical time domain reflectometer for distributed sensing of ultrasonic waves[J]. Proc SPIE, 2013, 8794: 87943F. DOI: 10.1117/12.2026081 CrossRef Google Scholar
[9]	孙振世. 基于分布式光纤振动传感的压力水管泄漏监测应用研究[D]. 成都: 电子科技大学, 2016. Sun Z S. Study on leakage monitor of pressure water pipe based on distributed optical fiber vibration sensing technology[D]. Chengdu: University of Electronic Science and Technology of China, 2016. Google Scholar
[10]	李信宇, 车前, 熊玉川, 等. 基于弱光栅阵列增强的Φ-OTDR传感系统性能分析[J]. 光电子·激光, 2019, 30(7): 673−677. DOI: 10.16136/j.joel.2019.07.0002 Li X Y, Che Q, Xiong Y C, et al. The analysis of improved phase-OTDR sensing system employing weak fiber Bragg grating array[J]. J Optoelectron·Laser, 2019, 30(7): 673−677. DOI: 10.16136/j.joel.2019.07.0002 CrossRef Google Scholar
[11]	吴慧娟, 刘欣雨, 饶云江. 基于Φ-OTDR的光纤分布式传感信号处理及应用[J]. 激光与光电子学进展, 2021, 58(13): 1306003−51. DOI: 10.3788/LOP202158.1306003 Wu H J, Liu X Y, Rao Y J. Processing and application of fiber optic distributed sensing signal based on Φ-OTDR[J]. Laser Optoelectron Prog, 2021, 58(13): 1306003−51. DOI: 10.3788/LOP202158.1306003 CrossRef Google Scholar
[12]	褚庆昕, 陈付昌. 多频带通滤波器技术(英文)[J]. 华南理工大学学报(自然科学版), 2012, 40(10): 219−226. DOI: 10.3969/j.issn.1000-565X.2012.10.031 Chu Q X, Chen F C. Multiband bandpass filter technologies[J]. J South China Univ Technol (Nat Sci Ed), 2012, 40(10): 219−226. DOI: 10.3969/j.issn.1000-565X.2012.10.031 CrossRef Google Scholar
[13]	张燕君, 刘文哲, 付兴虎, 等. 基于EMD-AWPP和HOSA-SVM算法的分布式光纤振动入侵信号的特征提取与识别[J]. 光谱学与光谱分析, 2016, 36(2): 577−582. DOI: 10.3964/j.issn.1000-0593(2016)02-0577-06 Zhang Y J, Liu W Z, Fu X H, et al. An extraction and recognition method of the distributed optical fiber vibration signal based on EMD-AWPP and HOSA-SVM algorithm[J]. Spectrosc Spectral Anal, 2016, 36(2): 577−582. DOI: 10.3964/j.issn.1000-0593(2016)02-0577-06 CrossRef Google Scholar
[14]	袁晓月, 谭中伟. 基于φ-OTDR的分布式光纤传感技术的现状与发展[J]. 光通信技术, 2018, 42(2): 23−26. DOI: 10.13921/j.cnki.issn1002-5561.2018.02.007 Yuan X Y, Tan Z W. Status and development of distributed optical fiber sensing technology based on φ-OTDR[J]. Opt Commun Technol, 2018, 42(2): 23−26. DOI: 10.13921/j.cnki.issn1002-5561.2018.02.007 CrossRef Google Scholar
[15]	金燊, 宋伟, 杨纯, 等. 120 km长距离分布式光纤振动传感系统[J]. 光通信研究, 2021(3): 20−24. DOI: 10.13756/j.gtxyj.2021.03.005 Jin S, Song W, Yang C, et al. 120 km long-distance distributed optical fiber vibration sensing system[J]. Study Opt Commun, 2021(3): 20−24. DOI: 10.13756/j.gtxyj.2021.03.005 CrossRef Google Scholar
[16]	卢斌, 王照勇, 郑汉荣, 等. 高空间分辨率长距离分布式光纤振动传感系统[J]. 中国激光, 2017, 44(10): 1015001. DOI: 10.3788/CJL201744.1015001 Lu B, Wang Z Y, Zheng H R, et al. High spatial resolution long distance distributed optical fiber vibration sensing system[J]. Chin J Lasers, 2017, 44(10): 1015001. DOI: 10.3788/CJL201744.1015001 CrossRef Google Scholar
[17]	Chow D M, Yang Z S, Soto M A, et al. Distributed forward Brillouin sensor based on local light phase recovery[J]. Nat Commun, 2018, 9(1): 2990. DOI: 10.1038/s41467-018-05410-2 CrossRef Google Scholar
[18]	潘亮, 刘琨, 江俊峰, 等. 分布式光纤振动和温度双物理量传感系统[J]. 中国激光, 2018, 45(1): 0110002. DOI: 10.3788/CJL201845.0110002 Pan L, Liu K, Jiang J F, et al. Distributed fiber-optic vibration and temperature sensing system[J]. Chin J Lasers, 2018, 45(1): 0110002. DOI: 10.3788/CJL201845.0110002 CrossRef Google Scholar
[19]	Liu S Q, Yu F H, Hong R, et al. Advances in phase-sensitive optical time-domain reflectometry[J]. Opto-Electron Adv, 2022, 5(3): 200078. DOI: 10.29026/oea.2022.200078 CrossRef Google Scholar
[20]	Zan W, Wang Y, Liu X, et al. Envelope extraction for vibration locating in coherent φ-OTDR[J]. Sensors, 2022, 22(3): 1197. DOI: 10.3390/s22031197 CrossRef Google Scholar
[21]	Li S, Qin Z G, Liu Z J, et al. Long-distance φ-OTDR with a flexible frequency response based on time division multiplexing[J]. Opt Express, 2021, 29(21): 32833−32841. DOI: 10.1364/OE.435883 CrossRef Google Scholar
[22]	Zhang M, Wang S, Zheng Y W, et al. Enhancement for φ-OTDR performance by using narrow linewidth light source and signal processing[J]. Photonic Sens, 2016, 6(1): 58−62. DOI: 10.1007/s13320-015-0283-7 CrossRef Google Scholar
[23]	Peng F, Wu H, Jia X H, et al. Ultra-long high-sensitivity φ-OTDR for high spatial resolution intrusion detection of pipelines[J]. Opt Express, 2014, 22(11): 13804−13810. DOI: 10.1016/j.optlaseng.2015.08.010. CrossRef Google Scholar
[24]	肖文哲, 程静, 张大伟, 等. 用于光纤干涉传感器的高稳定PGC解调技术[J]. 光电工程, 2022, 49(3): 210368. DOI: 10.12086/oee.2022.210368 Xiao W Z, Cheng J, Zhang D W, et al. High stability PGC demodulation technique for fiber-optic interferometric sensor[J]. Opto-Electron Eng, 2022, 49(3): 210368. DOI: 10.12086/oee.2022.210368 CrossRef Google Scholar
[25]	张永康, 尚盈, 王晨, 等. 分布式光纤入侵信号检测与识别[J]. 光电工程, 2021, 48(3): 200254. DOI: 10.12086/oee.2021.200254 Zhang Y K, Shang Y, Wang C, et al. Detection and recognition of distributed optical fiber intrusion signal[J]. Opto-Electron Eng, 2021, 48(3): 200254. DOI: 10.12086/oee.2021.200254 CrossRef Google Scholar
[26]	Liu T, Li H, He T, et al. Ultra-high resolution strain sensor network assisted with an LS-SVM based hysteresis model[J]. Opto-Electron Adv, 2021, 4(5): 200037. DOI: 10.29026/oea.2021.200037 CrossRef Google Scholar

View full references list

Cited By

Cited by

Periodical cited type(6)

1.	贾鹏，谢建东，楼盈天，杨晔，杨涛. 基于内调制的光纤干涉振动测量系统研究. 光电工程. 2025(01): 12-25 . 本站查看
2.	叶骁宇，闫鹏，蒋强，杜爱春. 深度学习模型在振动检测中的应用研究. 造纸装备及材料. 2025(02): 10-12 .
3.	毕灵月，王强，巫宇航. 基于自适应方差阈值算法的DTS合成气管道漏损检测与定位. 科学技术与工程. 2025(12): 5037-5044 .
4.	杨双权，董树林，金宁，王子荣，杨开宇，李晶，杨丹，徐曼. 螺钉预紧力变化对热像仪光轴稳定性的影响机理分析. 红外与激光工程. 2024(08): 125-136 .
5.	刘浩，杨剑，史然，王新功. 光纤振动深度学习算法在模式识别中的性能优化. 光学与光电技术. 2024(06): 121-128 .
6.	刘浩，杨剑，史然，王新功. 光纤振动深度学习算法在模式识别中的性能优化. 光学与光电技术. 2024(05): 121-128 .

Other cited types(1)

Author Information

Author Information
- Zhang Bozhi, 437049504@qq.com On this Site On Google Scholar
  - School of Precision Instrument and Opto-electronics Engineering, Tianjin University, Tianjin 300000, China
  - Key Laboratory of Opto-electronics Information Technology, Ministry of Education, Tianjin 300000, China
  - Tianjin Fiber Optic Sensing Engineering Center, Tianjin 300000, China
- Liu Ke On this Site On Google Scholar
  - Tianjin Qiu Shi Fiber Technologies Co., Ltd., Tianjin 300000, China
- Liu Kun On this Site On Google Scholar
  - School of Precision Instrument and Opto-electronics Engineering, Tianjin University, Tianjin 300000, China
  - Key Laboratory of Opto-electronics Information Technology, Ministry of Education, Tianjin 300000, China
  - Tianjin Fiber Optic Sensing Engineering Center, Tianjin 300000, China
- Jiang Junfeng On this Site On Google Scholar
  - School of Precision Instrument and Opto-electronics Engineering, Tianjin University, Tianjin 300000, China
  - Key Laboratory of Opto-electronics Information Technology, Ministry of Education, Tianjin 300000, China
  - Tianjin Fiber Optic Sensing Engineering Center, Tianjin 300000, China
- Zhang Man On this Site On Google Scholar
  - Tianjin Qiu Shi Fiber Technologies Co., Ltd., Tianjin 300000, China
- Corresponding author: Liu Tiegen, tgliu@tju.edu.cn On this Site On Google Scholar
  tgliu@tju.edu.cn
  - School of Precision Instrument and Opto-electronics Engineering, Tianjin University, Tianjin 300000, China
  - Key Laboratory of Opto-electronics Information Technology, Ministry of Education, Tianjin 300000, China
  - Tianjin Fiber Optic Sensing Engineering Center, Tianjin 300000, China

Copyright

The copyright belongs to the Institute of Optics and Electronics, Chinese Academy of Sciences, but the article content can be freely downloaded from this website and used for free in academic and research work.

About this Article

About this Article
DOI: 10.12086/oee.2023.220205

Cite this Article

Zhang Bozhi, Liu Ke, Liu Kun, Jiang Junfeng, Zhang Man, Liu Tiegen. Research on dynamic variance threshold algorithm based on distributed fiber vibration sensor system. Opto-Electronic Engineering 50, 220205 (2023). DOI: 10.12086/oee.2023.220205

Zhang Bozhi, Liu Ke, Liu Kun, Jiang Junfeng, Zhang Man, Liu Tiegen. Research on dynamic variance threshold algorithm based on distributed fiber vibration sensor system. Opto-Electronic Engineering 50, 220205 (2023). DOI: 10.12086/oee.2023.220205

Download Citation
Article History
- Received Date August 22, 2022
- Revised Date November 05, 2022
- Accepted Date November 27, 2022
- Available Online February 15, 2023
- Published Date February 15, 2023
Article Metrics

Article Views(8902) PDF Downloads(1021)
Share:

Related Articles
- Frequency-modulated continuous-wave laser interferometry displacement sensor based on centroid peak-finding
  
  Zhang Dengpan, Yan Mengchao, Shi Ancun, Li Gaochao, Zhao Xian, Wang Yongjie, Li Fang
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2023.220315
- Miniature computational spectral detection technology based on correlation value selection
  
  Yang Gang, Guo Yinghui, Pu Mingbo, Li Xiong, Luo Xiangang
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2022.220130
- An open-pit mine roadway obstacle warning method integrating the object detection and distance threshold model
  
  Lu Caiwu, Qi Fan, Ruan Shunling
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2020.190161
- Improved algorithm of Faster R-CNN based on double threshold-non-maximum suppression
  
  Hou Zhiqiang, Liu Xiaoyi, Yu Wangsheng, Ma Sugang
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2019.190159
- Sparse reconstruction of interferometric hyperspectral image based on adaptive threshold
  
  Wen Jia, Liu Mingwei, Cui Jun, Yan Shuxia
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2019.180443
- Fiber optic gyroscope threshold denoising based on EMD-LWT
  
  Dai Shaowu, Zheng Baidong, Dai Hongde, Nie Zijian
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2019.180333
- Research on image segmentation algorithm based on features of venous gray value
  
  Wang Dinghan, Feng Guilan, Wang Xiong, Wu Yufeng, Deng Maohua
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2018.180066
- Local adaptive threshold segmentation method for subapture spots of Shack-Hartmann sensor
  
  Li Xuxu, Li Xinyang, Wang Caixia
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2018.170699
- Compensation of gray value drift for ground-based MWIR measurement system
  
  Zhao Yun, Li Manliang, Cui Zhi, Sun Jingang, An Xueguang
  
  Opto-Electronic Engineering, DOI: 10.12086/oee.2018.170535
- Analysis on stitching overlap pixel threshold of one-orbit multi-strip agile remote sensing imaging
  
  Yue Xu, Huajun Feng, Zhihai Xu, Qi Li, Yueting Chen
  
  Opto-Electronic Engineering, DOI: 10.3969/j.issn.1003-501X.2017.11.005

Article Contents
Figures/Tables
References

View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint
View in article Downloads

Full-Size Img PowerPoint

[1]	Juarez J C, Maier E W, Choi K N, et al. Distributed fiber-optic intrusion sensor system[J]. J Lightwave Technol, 2005, 23(6): 2081−2087. DOI: 10.1109/JLT.2005.849924 CrossRef Google Scholar
[2]	Tan D J, Tian X Z, Sun W, et al. An oil and gas pipeline pre-warning system based on Φ-OTDR[J]. Proc SPIE, 2014, 9157: 91578W. DOI: 10.1117/12.2054698 CrossRef Google Scholar
[3]	吴慧娟, 陈忠权, 吕立冬, 等. 基于DOFVS的新型压力输水管道泄漏在线监测方法[J]. 仪器仪表学报, 2017, 38(1): 159−165. DOI: 10.3969/j.issn.0254-3087.2017.01.021 Wu H J, Chen Z Q, Lv L D, et al. Novel pressurized water pipe leak monitoring method based on the distributed optical fiber vibration sensor[J]. Chin J Sci Instrument, 2017, 38(1): 159−165. DOI: 10.3969/j.issn.0254-3087.2017.01.021 CrossRef Google Scholar
[4]	Bao X Y, Zhou D P, Baker C, et al. Recent development in the distributed fiber optic acoustic and ultrasonic detection[J]. J Lightwave Technol, 2017, 35(16): 3256−3267. DOI: 10.1109/JLT.2016.2612060 CrossRef Google Scholar
[5]	Duckworth G L, Ku E M. OptaSense distributed acoustic and seismic sensing using COTS fiber optic cables for infrastructure protection and counter terrorism[J]. Proc SPIE, 2013, 8711: 87110G. DOI: 10.1117/12.2017712 CrossRef Google Scholar
[6]	Taylor H F, Lee C E. Apparatus and method for fiber optic intrusion sensing: 5194847[P]. 1993-03-16. Google Scholar
[7]	梁可桢, 潘政清, 周俊, 等. 一种基于相位敏感光时域反射计的多参量振动传感器[J]. 中国激光, 2012, 39(8): 0805004. DOI: 10.3788/CJL201239.0805004 Liang K Z, Pan Z Q, Zhou J, et al. Multi-parameter vibration detection system based on phase sensitive optical time domain reflectometer[J]. Chin J Lasers, 2012, 39(8): 0805004. DOI: 10.3788/CJL201239.0805004 CrossRef Google Scholar
[8]	Martins H F, martin-Lopez S, Corredera P, et al. High visibility phase-sensitive optical time domain reflectometer for distributed sensing of ultrasonic waves[J]. Proc SPIE, 2013, 8794: 87943F. DOI: 10.1117/12.2026081 CrossRef Google Scholar
[9]	孙振世. 基于分布式光纤振动传感的压力水管泄漏监测应用研究[D]. 成都: 电子科技大学, 2016. Sun Z S. Study on leakage monitor of pressure water pipe based on distributed optical fiber vibration sensing technology[D]. Chengdu: University of Electronic Science and Technology of China, 2016. Google Scholar
[10]	李信宇, 车前, 熊玉川, 等. 基于弱光栅阵列增强的Φ-OTDR传感系统性能分析[J]. 光电子·激光, 2019, 30(7): 673−677. DOI: 10.16136/j.joel.2019.07.0002 Li X Y, Che Q, Xiong Y C, et al. The analysis of improved phase-OTDR sensing system employing weak fiber Bragg grating array[J]. J Optoelectron·Laser, 2019, 30(7): 673−677. DOI: 10.16136/j.joel.2019.07.0002 CrossRef Google Scholar
[11]	吴慧娟, 刘欣雨, 饶云江. 基于Φ-OTDR的光纤分布式传感信号处理及应用[J]. 激光与光电子学进展, 2021, 58(13): 1306003−51. DOI: 10.3788/LOP202158.1306003 Wu H J, Liu X Y, Rao Y J. Processing and application of fiber optic distributed sensing signal based on Φ-OTDR[J]. Laser Optoelectron Prog, 2021, 58(13): 1306003−51. DOI: 10.3788/LOP202158.1306003 CrossRef Google Scholar
[12]	褚庆昕, 陈付昌. 多频带通滤波器技术(英文)[J]. 华南理工大学学报(自然科学版), 2012, 40(10): 219−226. DOI: 10.3969/j.issn.1000-565X.2012.10.031 Chu Q X, Chen F C. Multiband bandpass filter technologies[J]. J South China Univ Technol (Nat Sci Ed), 2012, 40(10): 219−226. DOI: 10.3969/j.issn.1000-565X.2012.10.031 CrossRef Google Scholar
[13]	张燕君, 刘文哲, 付兴虎, 等. 基于EMD-AWPP和HOSA-SVM算法的分布式光纤振动入侵信号的特征提取与识别[J]. 光谱学与光谱分析, 2016, 36(2): 577−582. DOI: 10.3964/j.issn.1000-0593(2016)02-0577-06 Zhang Y J, Liu W Z, Fu X H, et al. An extraction and recognition method of the distributed optical fiber vibration signal based on EMD-AWPP and HOSA-SVM algorithm[J]. Spectrosc Spectral Anal, 2016, 36(2): 577−582. DOI: 10.3964/j.issn.1000-0593(2016)02-0577-06 CrossRef Google Scholar
[14]	袁晓月, 谭中伟. 基于φ-OTDR的分布式光纤传感技术的现状与发展[J]. 光通信技术, 2018, 42(2): 23−26. DOI: 10.13921/j.cnki.issn1002-5561.2018.02.007 Yuan X Y, Tan Z W. Status and development of distributed optical fiber sensing technology based on φ-OTDR[J]. Opt Commun Technol, 2018, 42(2): 23−26. DOI: 10.13921/j.cnki.issn1002-5561.2018.02.007 CrossRef Google Scholar
[15]	金燊, 宋伟, 杨纯, 等. 120 km长距离分布式光纤振动传感系统[J]. 光通信研究, 2021(3): 20−24. DOI: 10.13756/j.gtxyj.2021.03.005 Jin S, Song W, Yang C, et al. 120 km long-distance distributed optical fiber vibration sensing system[J]. Study Opt Commun, 2021(3): 20−24. DOI: 10.13756/j.gtxyj.2021.03.005 CrossRef Google Scholar
[16]	卢斌, 王照勇, 郑汉荣, 等. 高空间分辨率长距离分布式光纤振动传感系统[J]. 中国激光, 2017, 44(10): 1015001. DOI: 10.3788/CJL201744.1015001 Lu B, Wang Z Y, Zheng H R, et al. High spatial resolution long distance distributed optical fiber vibration sensing system[J]. Chin J Lasers, 2017, 44(10): 1015001. DOI: 10.3788/CJL201744.1015001 CrossRef Google Scholar
[17]	Chow D M, Yang Z S, Soto M A, et al. Distributed forward Brillouin sensor based on local light phase recovery[J]. Nat Commun, 2018, 9(1): 2990. DOI: 10.1038/s41467-018-05410-2 CrossRef Google Scholar
[18]	潘亮, 刘琨, 江俊峰, 等. 分布式光纤振动和温度双物理量传感系统[J]. 中国激光, 2018, 45(1): 0110002. DOI: 10.3788/CJL201845.0110002 Pan L, Liu K, Jiang J F, et al. Distributed fiber-optic vibration and temperature sensing system[J]. Chin J Lasers, 2018, 45(1): 0110002. DOI: 10.3788/CJL201845.0110002 CrossRef Google Scholar
[19]	Liu S Q, Yu F H, Hong R, et al. Advances in phase-sensitive optical time-domain reflectometry[J]. Opto-Electron Adv, 2022, 5(3): 200078. DOI: 10.29026/oea.2022.200078 CrossRef Google Scholar
[20]	Zan W, Wang Y, Liu X, et al. Envelope extraction for vibration locating in coherent φ-OTDR[J]. Sensors, 2022, 22(3): 1197. DOI: 10.3390/s22031197 CrossRef Google Scholar
[21]	Li S, Qin Z G, Liu Z J, et al. Long-distance φ-OTDR with a flexible frequency response based on time division multiplexing[J]. Opt Express, 2021, 29(21): 32833−32841. DOI: 10.1364/OE.435883 CrossRef Google Scholar
[22]	Zhang M, Wang S, Zheng Y W, et al. Enhancement for φ-OTDR performance by using narrow linewidth light source and signal processing[J]. Photonic Sens, 2016, 6(1): 58−62. DOI: 10.1007/s13320-015-0283-7 CrossRef Google Scholar
[23]	Peng F, Wu H, Jia X H, et al. Ultra-long high-sensitivity φ-OTDR for high spatial resolution intrusion detection of pipelines[J]. Opt Express, 2014, 22(11): 13804−13810. DOI: 10.1016/j.optlaseng.2015.08.010. CrossRef Google Scholar
[24]	肖文哲, 程静, 张大伟, 等. 用于光纤干涉传感器的高稳定PGC解调技术[J]. 光电工程, 2022, 49(3): 210368. DOI: 10.12086/oee.2022.210368 Xiao W Z, Cheng J, Zhang D W, et al. High stability PGC demodulation technique for fiber-optic interferometric sensor[J]. Opto-Electron Eng, 2022, 49(3): 210368. DOI: 10.12086/oee.2022.210368 CrossRef Google Scholar
[25]	张永康, 尚盈, 王晨, 等. 分布式光纤入侵信号检测与识别[J]. 光电工程, 2021, 48(3): 200254. DOI: 10.12086/oee.2021.200254 Zhang Y K, Shang Y, Wang C, et al. Detection and recognition of distributed optical fiber intrusion signal[J]. Opto-Electron Eng, 2021, 48(3): 200254. DOI: 10.12086/oee.2021.200254 CrossRef Google Scholar
[26]	Liu T, Li H, He T, et al. Ultra-high resolution strain sensor network assisted with an LS-SVM based hysteresis model[J]. Opto-Electron Adv, 2021, 4(5): 200037. DOI: 10.29026/oea.2021.200037 CrossRef Google Scholar

Frequency-modulated continuous-wave laser interferometry displacement sensor based on centroid peak-finding

Zhang Dengpan, Yan Mengchao, Shi Ancun, Li Gaochao, Zhao Xian, Wang Yongjie, Li Fang

Opto-Electronic Engineering, DOI: 10.12086/oee.2023.220315
Miniature computational spectral detection technology based on correlation value selection

Yang Gang, Guo Yinghui, Pu Mingbo, Li Xiong, Luo Xiangang

Opto-Electronic Engineering, DOI: 10.12086/oee.2022.220130
An open-pit mine roadway obstacle warning method integrating the object detection and distance threshold model

Lu Caiwu, Qi Fan, Ruan Shunling

Opto-Electronic Engineering, DOI: 10.12086/oee.2020.190161
Improved algorithm of Faster R-CNN based on double threshold-non-maximum suppression

Hou Zhiqiang, Liu Xiaoyi, Yu Wangsheng, Ma Sugang

Opto-Electronic Engineering, DOI: 10.12086/oee.2019.190159
Sparse reconstruction of interferometric hyperspectral image based on adaptive threshold

Wen Jia, Liu Mingwei, Cui Jun, Yan Shuxia

Opto-Electronic Engineering, DOI: 10.12086/oee.2019.180443
Fiber optic gyroscope threshold denoising based on EMD-LWT

Dai Shaowu, Zheng Baidong, Dai Hongde, Nie Zijian

Opto-Electronic Engineering, DOI: 10.12086/oee.2019.180333
Research on image segmentation algorithm based on features of venous gray value

Wang Dinghan, Feng Guilan, Wang Xiong, Wu Yufeng, Deng Maohua

Opto-Electronic Engineering, DOI: 10.12086/oee.2018.180066
Local adaptive threshold segmentation method for subapture spots of Shack-Hartmann sensor

Li Xuxu, Li Xinyang, Wang Caixia

Opto-Electronic Engineering, DOI: 10.12086/oee.2018.170699
Compensation of gray value drift for ground-based MWIR measurement system

Zhao Yun, Li Manliang, Cui Zhi, Sun Jingang, An Xueguang

Opto-Electronic Engineering, DOI: 10.12086/oee.2018.170535
Analysis on stitching overlap pixel threshold of one-orbit multi-strip agile remote sensing imaging

Yue Xu, Huajun Feng, Zhihai Xu, Qi Li, Yueting Chen

Opto-Electronic Engineering, DOI: 10.3969/j.issn.1003-501X.2017.11.005

Research on dynamic variance threshold algorithm based on distributed fiber vibration sensor system

Abstract

Keywords

1. 引　言

2. 理论推导

2.1 ϕ-OTDR原理分析

2.2 动态方差阈值算法

2.2.1 带通滤波

2.2.2 方差分析

2.2.3 高斯模糊

3. 实验结果

3.1 噪声分析

3.2 平均模糊与高斯模糊比较

3.3 使用并行编程技术提高运算速度

4. 数据分析

5. 结　论

利益冲突

References

Cited by

Periodical cited type(6)

Other cited types(1)

Author Information

Zhang Bozhi, 437049504@qq.com On this Site On Google Scholar

Liu Ke On this Site On Google Scholar

Liu Kun On this Site On Google Scholar

Jiang Junfeng On this Site On Google Scholar

Zhang Man On this Site On Google Scholar

Corresponding author: Liu Tiegen, tgliu@tju.edu.cn On this Site On Google Scholar

Copyright

About this Article

Cite this Article

Article History

Article Metrics

Links

Catalog

Corresponding author: Liu Tiegen, tgliu@tju.edu.cn

Manuscript Submission

More Content

Legal & Privacy

Research on dynamic variance threshold algorithm based on distributed fiber vibration sensor system

Abstract

Keywords

1. 引 言

2. 理论推导

2.1 ϕ-OTDR原理分析

2.2 动态方差阈值算法

2.2.1 带通滤波

2.2.2 方差分析

2.2.3 高斯模糊

3. 实验结果

3.1 噪声分析

3.2 平均模糊与高斯模糊比较

3.3 使用并行编程技术提高运算速度

4. 数据分析

5. 结 论

利益冲突

References

Cited by

Periodical cited type(6)

Other cited types(1)

Author Information

Zhang Bozhi, 437049504@qq.com On this SiteOn Google Scholar

Liu Ke On this SiteOn Google Scholar

Liu Kun On this SiteOn Google Scholar

Jiang Junfeng On this SiteOn Google Scholar

Zhang Man On this SiteOn Google Scholar

Corresponding author: Liu Tiegen, tgliu@tju.edu.cn On this SiteOn Google Scholar

Copyright

About this Article

Cite this Article

Article History

Article Metrics

Related Articles

Links

Related Articles

Catalog

Corresponding author: Liu Tiegen, tgliu@tju.edu.cn

Manuscript Submission

More Content

Legal & Privacy

Export File

Citation

Format

Content

WeChat Qrcode

1. 引　言

5. 结　论

Zhang Bozhi, 437049504@qq.com On this Site On Google Scholar

Liu Ke On this Site On Google Scholar

Liu Kun On this Site On Google Scholar

Jiang Junfeng On this Site On Google Scholar

Zhang Man On this Site On Google Scholar

Corresponding author: Liu Tiegen, tgliu@tju.edu.cn On this Site On Google Scholar