E-mail Alert
RSS
| Citation: |
Porfirev A, Khonina S, Ustinov A, Ivliev N, Golub I. Vectorial spin-orbital Hall effect of light upon tight focusing and its experimental observation in azopolymer films. Opto-Electron Sci 2, 230014 (2023). doi: 10.29026/oes.2023.230014
|
Vectorial spin-orbital Hall effect of light upon tight focusing and its experimental observation in azopolymer films
-
Abstract
Hall effect of light is a result of symmetry breaking in spin and/or orbital angular momentum (OAM) possessing optical system and is caused by e.g. refractive index gradient/interface between media or focusing of a spatially asymmetrical beam, similar to the electric field breaking the symmetry in spin Hall effect for electrons. The angular momentum (AM) conservation law in the ensuing asymmetric system dictates redistribution of spin and orbital angular momentum, and is manifested in spin-orbit, orbit-orbit, and orbit-spin conversions and reorganization, i.e. spin-orbit and orbit-orbit interaction. This AM restructuring in turn requires shifts of the barycenter of the electric field of light. In the present study we show, both analytically and by numerical simulation, how different electric field components are displaced upon tight focusing of an asymmetric light beam having OAM and spin. The relation between field components shifts and the AM components shifts/redistribution is presented too. Moreover, we experimentally demonstrate, for the first time, to the best of our knowledge, the spin-orbit Hall effect of light upon tight focusing in free space. This is achieved using azopolymers as a media detecting longitudinal or z component of the electrical field of light. These findings elucidate the Hall effect of light and may broaden the spectrum of its applications. -
-
References
[1] Liu L, Chen SS, Lin ZZ, Zhang X. A symmetry-breaking phase in two-dimensional FeTe2 with ferromagnetism above room temperature. J Phys Chem Lett 11, 7893–7900 (2020). doi: 10.1021/acs.jpclett.0c01911 [2] Córdova C, Ohmori K, Rudelius T. Generalized symmetry breaking scales and weak gravity conjectures. J High Energy Phys 2022, 154 (2022). [3] Devínsky F. Chirality and the origin of life. Symmetry 13, 2277 (2021). doi: 10.3390/sym13122277 [4] Yang SH, Naaman R, Paltiel Y, Parkin SSP. Chiral spintronics. Nat Rev Phys 3, 328–343 (2021). doi: 10.1038/s42254-021-00302-9 [5] Cheng JH, Zhang Z, Mei W, Cao Y, Ling XH et al. Symmetry-breaking enabled topological phase transitions in spin-orbit optics. Opt Express 31, 23621–23630 (2023). doi: 10.1364/OE.494534 [6] Baranova NB, Savchenko AY, Zel’dovich BY. Transverse shift of a focal spot due to switching of the sign of circular polarization. JETP Lett 59, 232–234 (1994). [7] Aiello A, Lindlein N, Marquardt C, Leuchs G. Transverse angular momentum and geometric spin hall effect of light. Phys Rev Lett 103, 100401 (2009). doi: 10.1103/PhysRevLett.103.100401 [8] Bliokh KY, Alonso MA, Ostrovskaya EA, Aiello A. Angular momenta and spin-orbit interaction of nonparaxial light in free space. Phys Rev A 82, 063825 (2010). doi: 10.1103/PhysRevA.82.063825 [9] Zhu WG, She WL. Transverse angular momentum and transverse barycenter shift of a focused light field due to nonuniform input angular momentum. Opt Lett 39, 1337–1340 (2014). doi: 10.1364/OL.39.001337 [10] Khonina SN, Golub I. Vectorial spin Hall effect of light upon tight focusing. Opt Lett 47, 2166–2169 (2022). doi: 10.1364/OL.457507 [11] Porfirev A, Khonina S, Kuchmizhak A. Light–matter interaction empowered by orbital angular momentum: control of matter at the micro-and nanoscale. Prog Quantum Electron 88, 100459 (2023). doi: 10.1016/j.pquantelec.2023.100459 [12] Bliokh KY, Rodríguez-Fortuño FJ, Nori F, Zayats AV. Spin–orbit interactions of light. Nat Photonics 9, 796–808 (2015). doi: 10.1038/nphoton.2015.201 [13] Khonina SN, Golub I. Breaking the symmetry to structure light. Opt Lett 46, 2605–2608 (2021). doi: 10.1364/OL.423660 [14] Zhang Z, Mei W, Cheng JH, Tan YW, Dai ZP et al. Revisiting vortex generation in the spin-orbit interactions of refraction and focusing of light. Phys Rev A 106, 063520 (2022). doi: 10.1103/PhysRevA.106.063520 [15] Richards B, Wolf E. Electromagnetic diffraction in optical systems II. Structure of the image field in an aplanatic system. Proc Roy Soc A:Math Phys Sci 253, 358–379 (1959). [16] Pereira SF, van de Nes AS. Superresolution by means of polarisation, phase and amplitude pupil masks. Opt Commun 234, 119–124 (2004). doi: 10.1016/j.optcom.2004.02.020 [17] Bokor N, Davidson N. A three dimensional dark focal spot uniformly surrounded by light. Opt Commun 279, 229–234 (2007). doi: 10.1016/j.optcom.2007.07.014 [18] Khonina SN, Volotovskiy SG, Fidirko NS. Iterative approach to solve the inverse diffraction problem under sharp focusing conditions. Opt Mem Neural Netw 26, 18–25 (2017). doi: 10.3103/S1060992X17010040 [19] Mansuripur M. Certain computational aspects of vector diffraction problems. J Opt Soc Am A 6, 786–805 (1989). doi: 10.1364/JOSAA.6.000786 [20] Kogelnik H, Li T. Laser beams and resonators. Appl Opt 5, 1550–1567 (1966). doi: 10.1364/AO.5.001550 [21] Enderlein J, Pampaloni F. Unified operator approach for deriving Hermite–Gaussian and Laguerre–Gaussian laser modes. J Opt Soc Am A 21, 1553–1558 (2004). doi: 10.1364/JOSAA.21.001553 [22] Volotovskiy SG, Karpeev SV, Khonina SN. Algorithm for reconstructing complex coefficients of Laguerre–Gaussian modes from the intensity distribution of their coherent superposition. Comput Opt 44, 352–362 (2020). [23] Goodman JW. Introduction to Fourier Optics (McGraw-Hill, San Francisco, 1968). [24] Marcuse D. Light Transmission Optics 2nd ed (Van Nostrand Reinhold, New York, 1982). [25] Han L, Liu S, Li P, Zhang Y, Cheng HC et al. Catalystlike effect of orbital angular momentum on the conversion of transverse to three-dimensional spin states within tightly focused radially polarized beams. Phys. Rev. A 97, 053802 (2018). doi: 10.1103/PhysRevA.97.053802 [26] Meshalkin A, Losmanschii C, Prisacar A, Achimova E, Abashkin V et al. Carbazole-based azopolymers as media for polarization holographic recording. Adv Phys Res 1, 86–98 (2019). [27] Priimagi A, Shevchenko A. Azopolymer-based micro-and nanopatterning for photonic applications. J Polym Sci Part B Polym Phys 52, 163–182 (2014). doi: 10.1002/polb.23390 [28] Sekkat Z, Wood J, Aust EF, Knoll W, Volksen W et al. Light-induced orientation in a high glass transition temperature polyimide with polar azo dyes in the side chain. J Opt Soc Am B 13, 1713–1724 (1996). doi: 10.1364/JOSAB.13.001713 [29] Sekkat Z, Kawata S. Laser nanofabrication in photoresists and azopolymers. Laser Photonics Rev 8, 1–26 (2014). doi: 10.1002/lpor.201200081 [30] Sava I, Hurduc N, Sacarescu L, Apostol I, Damian V. Study of the nanostructuration capacity of some azopolymers with rigid or flexible chains. High Perform Polym 25, 13–24 (2013). doi: 10.1177/0954008312454151 [31] Ishitobi H, Nakamura I, Kobayashi TA, Hayazawa N, Sekkat Z et al. Nanomovement of azo polymers induced by longitudinal fields. ACS Photonics 1, 190–197 (2014). doi: 10.1021/ph400052b [32] Porfirev A, Khonina S, Ivliev N, Meshalkin A, Achimova E et al. Writing and reading with the longitudinal component of light using carbazole-containing azopolymer thin films. Sci Rep 12, 3477 (2022). doi: 10.1038/s41598-022-07440-9 [33] Porfirev AP, Khonina SN, Khorin PA, Ivliev NA. Polarization-sensitive direct laser patterning of azopolymer thin films with vortex beams. Opt Lett 47, 5080–5083 (2022). doi: 10.1364/OL.471236 [34] Porfirev AP, Ivliev NA, Fomchenkov SA, Khonina SN. Multi-spiral laser patterning of azopolymer thin films for generation of orbital angular momentum light. Nanomaterials 13, 612 (2023). doi: 10.3390/nano13030612 [35] Ambrosio A, Marrucci L, Borbone F, Roviello A, Maddalena P. Light-induced spiral mass transport in azo-polymer films under vortex-beam illumination. Nat Commun 3, 989 (2012). doi: 10.1038/ncomms1996 [36] Sekkat Z. Vectorial motion of matter induced by light fueled molecular machines. OSA Continuum 1, 668–681 (2018). doi: 10.1364/OSAC.1.000668 [37] Sekkat Z. Model for athermal enhancement of molecular mobility in solid polymers by light. Phys Rev E 102, 032501 (2020). doi: 10.1103/PhysRevE.102.032501 [38] Masuda K, Shinozaki R, Kinezuka Y, Lee J, Ohno S et al. Nanoscale chiral surface relief of azo-polymers with nearfield OAM light. Opt Express 26, 22197–22207 (2018). doi: 10.1364/OE.26.022197 [39] Masuda K, Shinozaki R, Shiraishi A, Ichijo M, Yamane K et al. Picosecond optical vortex-induced chiral surface relief in an azo-polymer film. J Nanophoton 14, 016012 (2020). -
Access History
Figures(11)
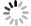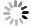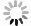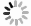
Article Metrics
Export File
Citation
Porfirev A, Khonina S, Ustinov A, Ivliev N, Golub I. Vectorial spin-orbital Hall effect of light upon tight focusing and its experimental observation in azopolymer films. Opto-Electron Sci 2, 230014 (2023). doi: 10.29026/oes.2023.230014
Format
Content
DownLoad:
-
Figure 1.
Numerical investigation of vectorial spin-orbital Hall effect of light upon tight focusing: (a) spatial frequency domain in Cartesian coordinates, (b–d) on- and off-axis propagation of a circularly polarized first-order optical vortex beam. The symmetry breaking in the longitudinal component and extrinsic OAM
$L_z^{{\rm{ext}}}$ -
Figure 2.
Comparison of asymmetry in focusing a shifted vortex beam with m=±1 order for x-linear polarization.
-
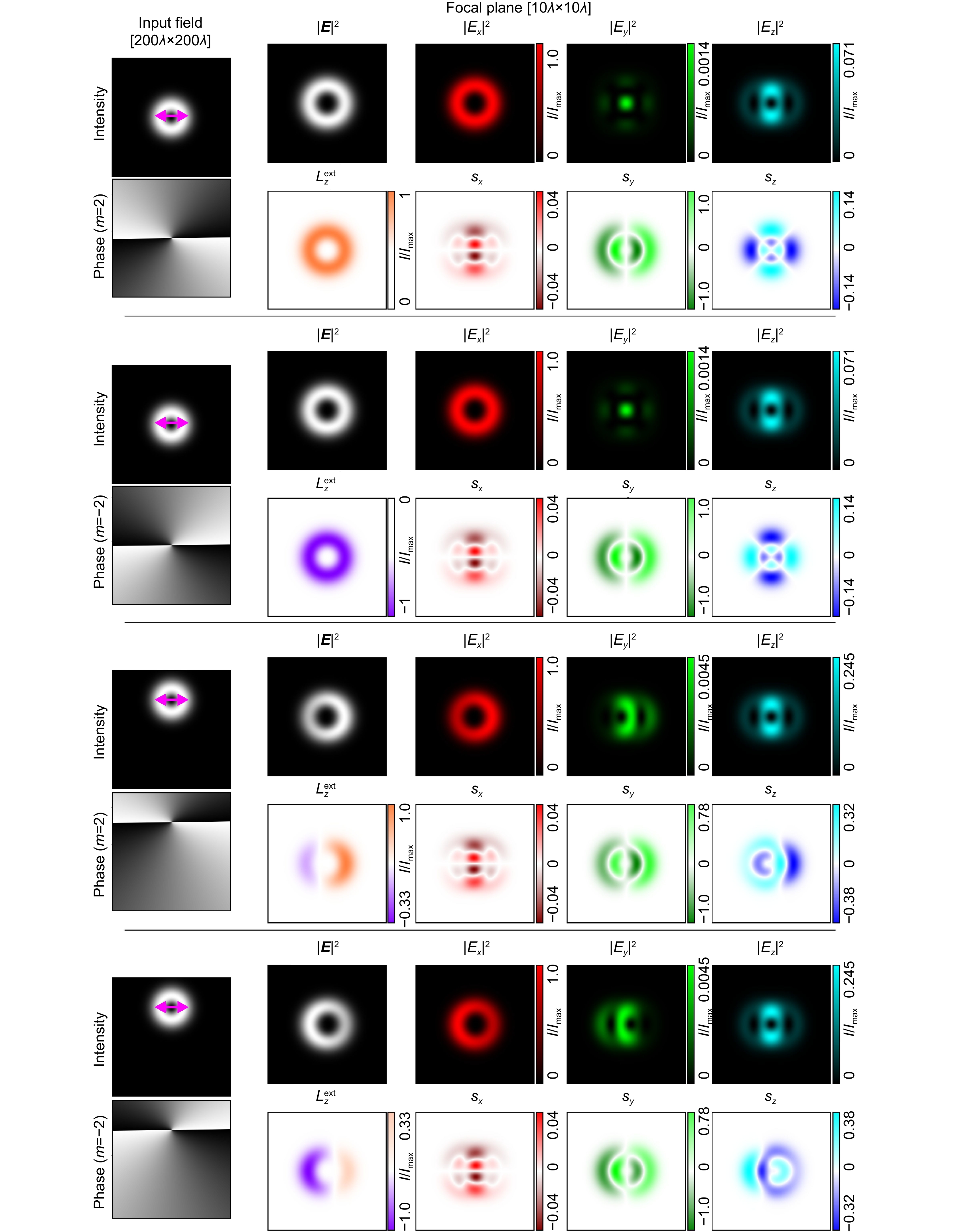
Figure 3.
Comparison of asymmetry in focusing a shifted vortex beam with m=±2 order for x-linear polarization.
-
Figure 4.
Comparison of asymmetry in focusing a shifted vortex beam with m=±1 order for y-linear polarization.
-
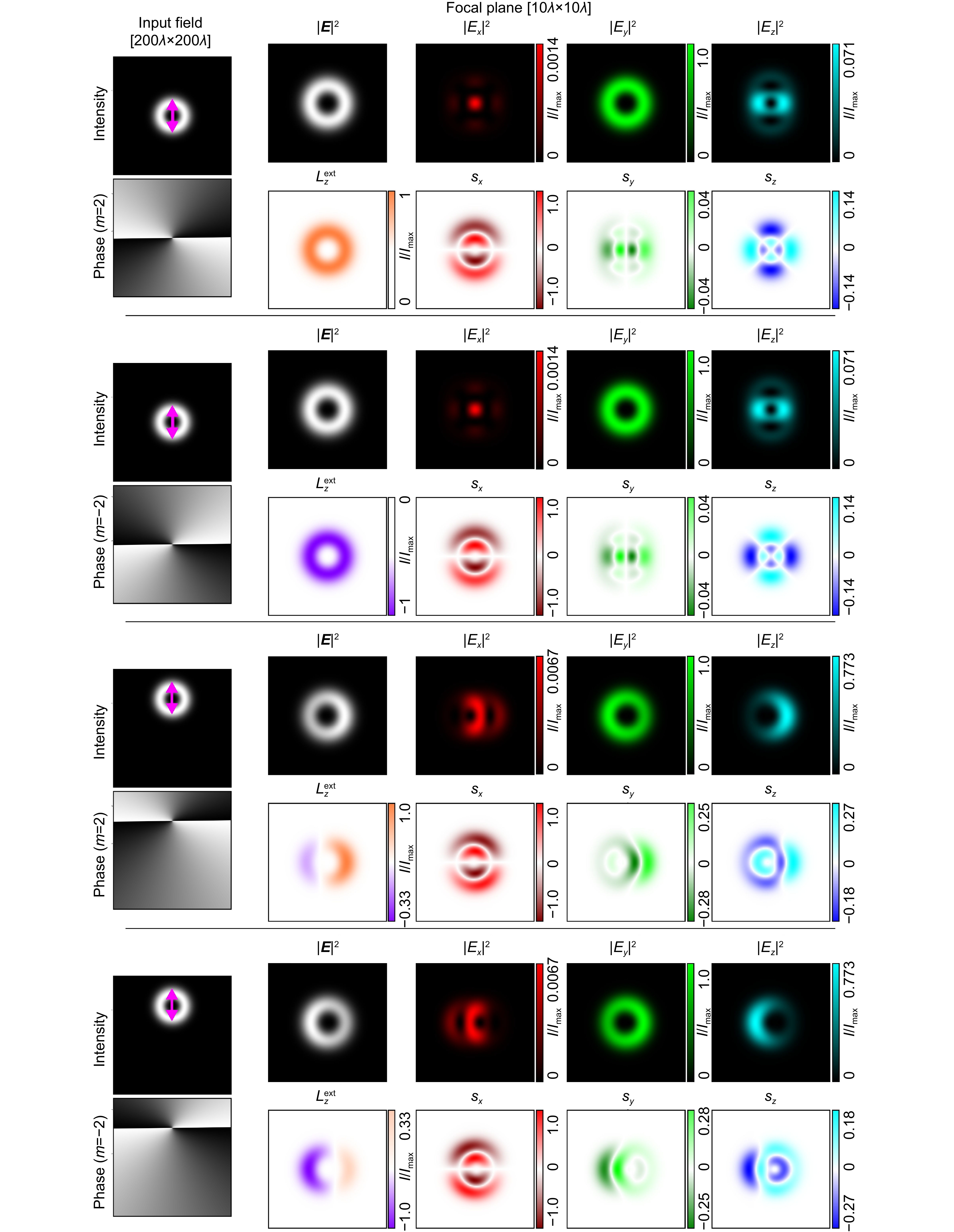
Figure 5.
Comparison of asymmetry in focusing a shifted vortex beam with m=±2 order for y-linear polarization.
-
Figure 6.
Comparison of asymmetry in focusing a shifted vortex beam with m=+1 order for “±” -circular polarization.
-
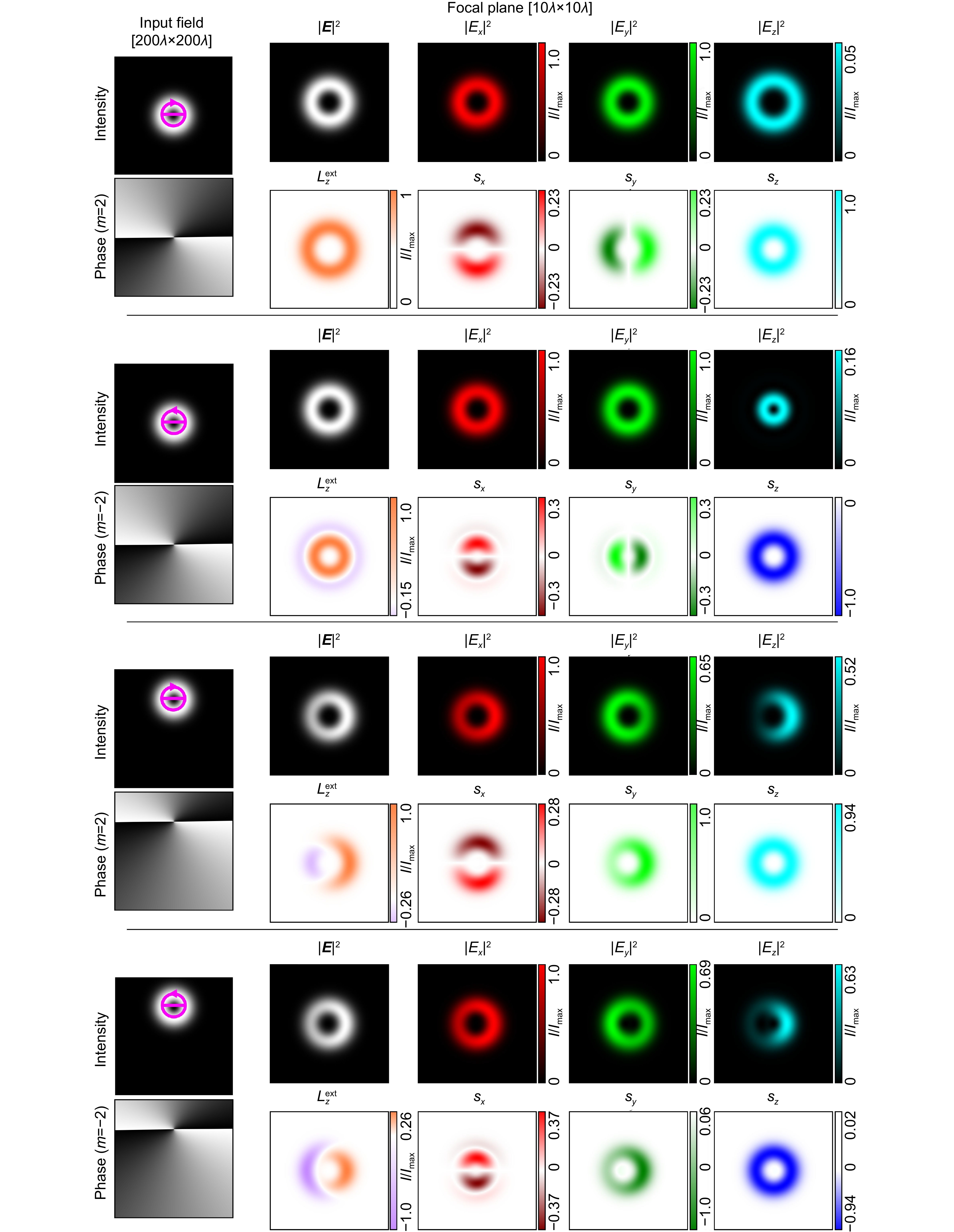
Figure 7.
Comparison of asymmetry in focusing a shifted vortex beam with m=+2 order for “±”-circular polarization.
-
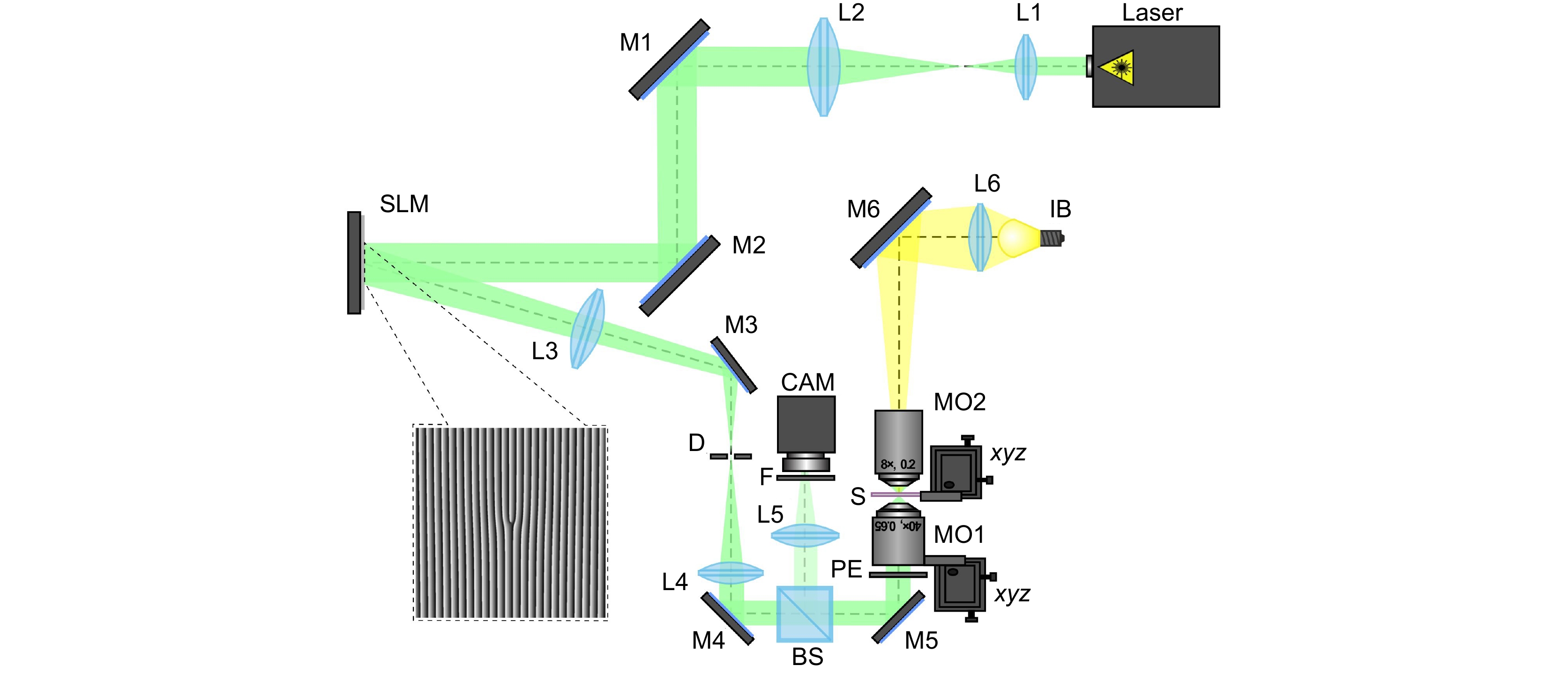
Figure 8.
The experimental setup for laser printing. Laser is a solid-state laser (λ=532 nm); L1, L2, L3, L4, L5, and L6 are spherical lenses (f1=25 mm, f2=150 mm, f3=500 mm, f4=400 mm, f5=150 mm, and f6=50 mm); M1, M2, M3, M4, M5, and M6 are mirrors, SLM is a reflective spatial light modulator (HOLOEYE PLUTO VIS); D is a circular diaphragm, BS is a beam splitter, PE is a polarizing element (a half wave or a quarter wave plate), MO1 and MO2 are microobjectives (NA=0.65 and 0.1); S is a glass substrate with a thin azopolymer film; xyz is a three-axis (XYZ) translation stage, IB is a light bulb, F is a neutral density filter, CAM is a ToupCam UCMOS08000KPB video camera. The inset shows an example of a phase mask realized with the SLM and used for the generation of a first-order OV beam.
-
Figure 9.
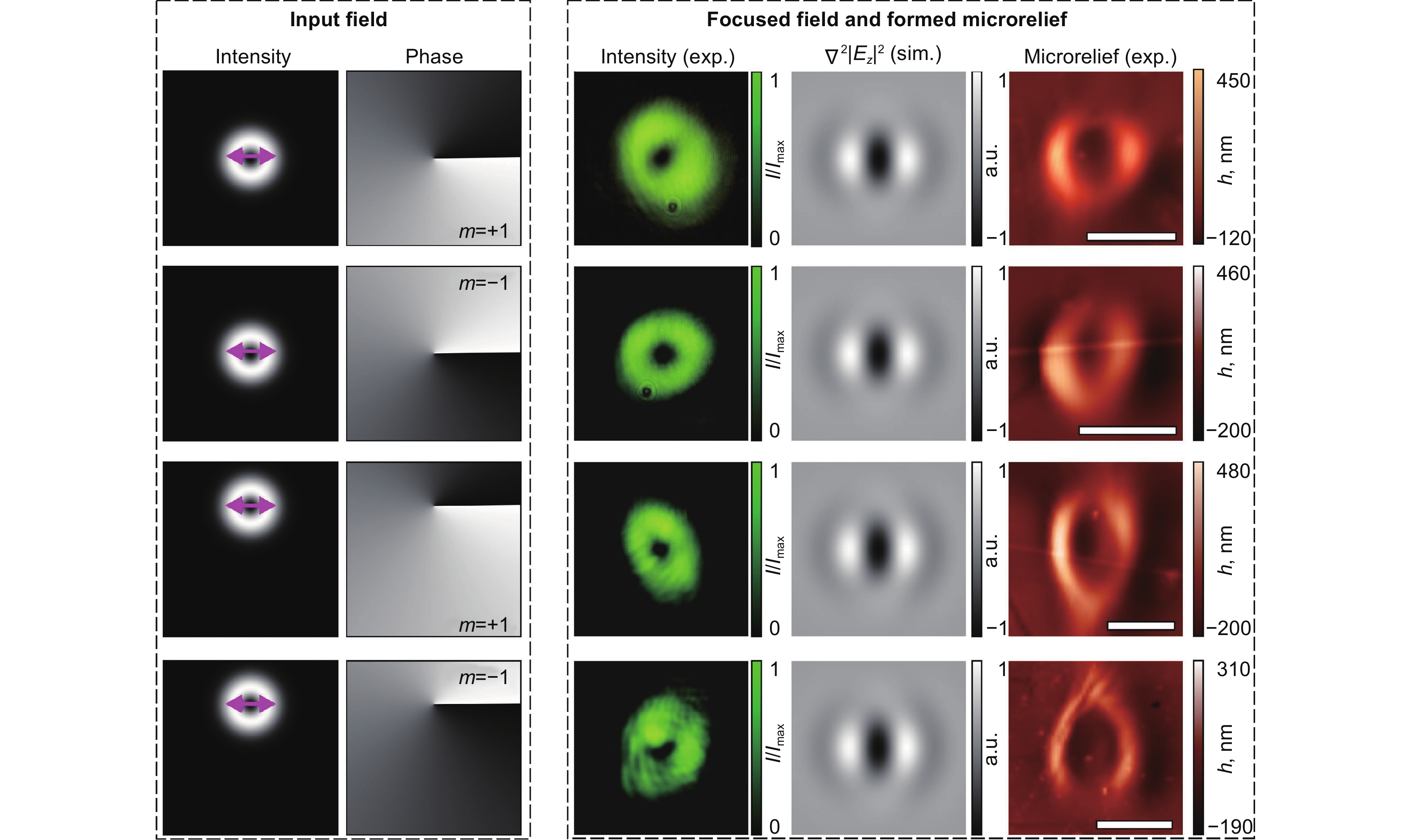
Laser patterning of an azopolymer thin film with x-linearly polarized on- and off-axis OV beams of ±1 order. The right part of the figure shows the experimentally generated intensity distribution, numerically calculated distribution of
$ {\nabla } $ -
Figure 11.
Laser patterning of an azopolymer thin film with right- and left handed circularly polarized on- and off-axis OV beams of ±1 order. The right part of the figure shows the experimentally generated intensity distribution, numerically calculated distribution of
$ {\nabla }$ -
Figure 10.
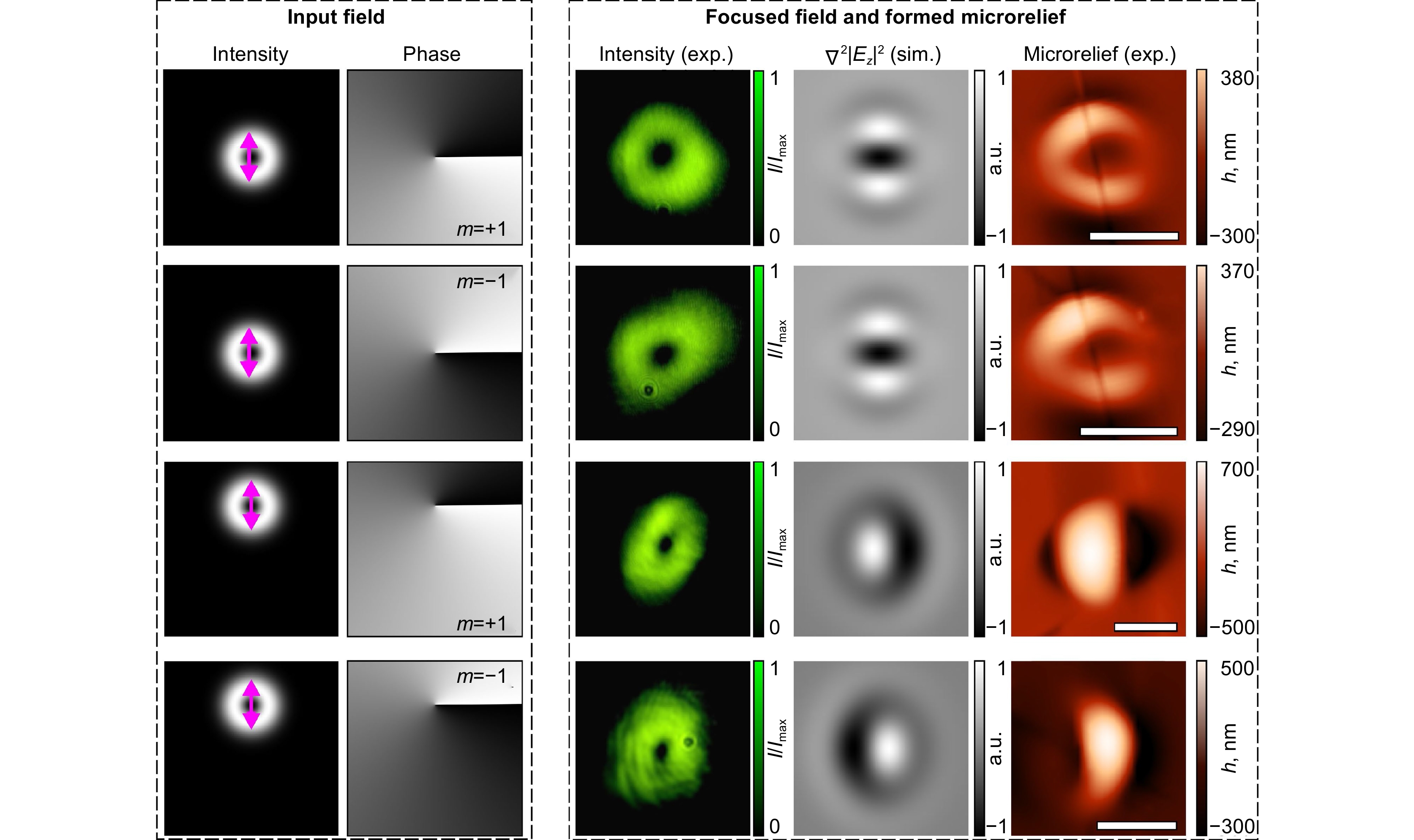
Laser patterning of an azopolymer thin film with y-linearly polarized on- and off-axis OV beams of ±1 order. The right part of the figure shows the experimentally generated intensity distribution, numerically calculated distribution of
$ {\nabla }$
