E-mail Alert
RSS
| Citation: |
Lu QB, Xiao QX, Liu CX, Wang YN, Zhu QX et al. Inverse design and realization of an optical cavity-based displacement transducer with arbitrary responses. Opto-Electron Adv 6, 220018 (2023). doi: 10.29026/oea.2023.220018
|
Inverse design and realization of an optical cavity-based displacement transducer with arbitrary responses
-
Abstract
Optical cavity has long been critical for a variety of applications ranging from precise measurement to spectral analysis. A number of theories and methods have been successful in describing the optical response of a stratified optical cavity, while the inverse problem, especially the inverse design of a displacement sensitive cavity, remains a significant challenge due to the cost of computation and comprehensive performance requirements. This paper reports a novel inverse design methodology combining the characteristic matrix method, mixed-discrete variables optimization algorithm, and Monte Carlo method-based tolerance analysis. The material characteristics are indexed to enable the mixed-discrete variables optimization, which yields considerable speed and efficiency improvements. This method allows arbitrary response adjustment with technical feasibility and gives a glimpse into the analytical characterization of the optical response. Two entirely different light-displacement responses, including an asymmetric sawtooth-like response and a highly symmetric response, are dug out and experimentally achieved, which fully confirms the validity of the method. The compact Fabry-Perot cavities have a good balance between performance and feasibility, making them promising candidates for displacement transducers. More importantly, the proposed inverse design paves the way for a universal design of optical cavities, or even nanophotonic devices. -
-
References
[1] Balle TJ, Flygare WH. Fabry-Perot cavity pulsed fourier transform microwave spectrometer with a pulsed nozzle particle source. Rev Sci Instrum 52, 33–45 (1981). doi: 10.1063/1.1136443 [2] Liang WJ, Bockrath M, Bozovic D, Hafner JH, Tinkham M et al. Fabry-Perot interference in a nanotube electron waveguide. Nature 411, 665–669 (2001). doi: 10.1038/35079517 [3] Luo XG, Tsai DP, Gu M, Hong MH. Subwavelength interference of light on structured surfaces. Adv Opt Photonics 10, 757–842 (2018). doi: 10.1364/AOP.10.000757 [4] Munkhbat B, Canales A, Küçüköz B, Baranov DG, Shegai TO. Tunable self-assembled Casimir microcavities and polaritons. Nature 597, 214–219 (2021). doi: 10.1038/s41586-021-03826-3 [5] Kouh T, Karabacak D, Kim DH, Ekinci KL. Diffraction effects in optical interferometric displacement detection in nanoelectromechanical systems. Appl Phys Lett 86, 013106 (2005). doi: 10.1063/1.1843289 [6] Lu QB, Wang C, Bai J, Wang KW, Lian WX et al. Subnanometer resolution displacement sensor based on a grating interferometric cavity with intensity compensation and phase modulation. Appl Opt 54, 4188–4196 (2015). doi: 10.1364/AO.54.004188 [7] De Groot PJ. A review of selected topics in interferometric optical metrology. Rep Prog Phys 82, 056101 (2019). doi: 10.1088/1361-6633/ab092d [8] Teh PC, Petropoulos P, Ibsen M, Richardson DJ. A comparative study of the performance of seven- and 63-chip optical code-division multiple-access encoders and decoders based on superstructured fiber Bragg gratings. J Lightwave Technol 19, 1352–1365 (2001). doi: 10.1109/50.948283 [9] Kimura A, Gao W, Kim W, Hosono K, Shimizu Y et al. A sub-nanometric three-axis surface encoder with short-period planar gratings for stage motion measurement. Precis Eng 36, 576–585 (2012). doi: 10.1016/j.precisioneng.2012.04.005 [10] Yu HY, Chen XL, Liu CJ, Cai GG, Wang WD. A survey on the grating based optical position encoder. Opt Laser Technol 143, 107352 (2021). doi: 10.1016/j.optlastec.2021.107352 [11] Kiesel N, Blaser F, Delić U, Grass D, Kaltenbaek R et al. Cavity cooling of an optically levitated submicron particle. Natl Proc Acad Sci USA 110, 14180–14185 (2013). doi: 10.1073/pnas.1309167110 [12] Hall NA, Okandan M, Littrell R, Serkland DK, Keeler GA et al. Micromachined accelerometers with optical interferometric read-out and integrated electrostatic actuation. J Microelectromech Syst 17, 37–44 (2008). doi: 10.1109/JMEMS.2007.910243 [13] Lu QB, Bai J, Wang KW, He SL. Design, optimization, and realization of a high-performance MOEMS accelerometer from a double-device-layer SOI wafer. J Microelectromech Syst 26, 859–869 (2017). doi: 10.1109/JMEMS.2017.2693341 [14] Li CH, Benedick AJ, Fendel P, Glenday AG, Kärtner FX et al. A laser frequency comb that enables radial velocity measurements with a precision of 1 cm s-1. Nature 452, 610–612 (2008). doi: 10.1038/nature06854 [15] Berkovic G, Shafir E. Optical methods for distance and displacement measurements. Adv Opt Photonics 4, 441–471 (2012). doi: 10.1364/AOP.4.000441 [16] Sun B, Wang YP, Qu JL, Liao CR, Yin GL et al. Simultaneous measurement of pressure and temperature by employing Fabry-Perot interferometer based on pendant polymer droplet. Opt Express 23, 1906–1911 (2015). doi: 10.1364/OE.23.001906 [17] Lu QB, Wang YA, Wang XX, Yao Y, Wang XW et al. Review of micromachined optical accelerometers: from mg to sub-μg. Opto-Electron Adv 4, 200045 (2021). [18] Dai P, Wang YS, Hu YQ, De Groot CH, Muskens O et al. Accurate inverse design of Fabry-Perot-cavity-based color filters far beyond sRGB via a bidirectional artificial neural network. Photonics Res 9, B236–B246 (2021). doi: 10.1364/PRJ.415141 [19] Berreman DW. Optics in stratified and anisotropic media: 4×4-matrix formulation. J Opt Soc Am 62, 502–510 (1972). doi: 10.1364/JOSA.62.000502 [20] Monzón JJ, Sánchez-Soto LL, Bernabeu E. Influence of coating thickness on the performance of a Fabry-Perot Interferometer. Appl Opt 30, 4126–4132 (1991). doi: 10.1364/AO.30.004126 [21] Monzón JJ, Sánchez-Soto LL, Csilling Á. Method for coating optimization in a Fabry-Perot interferometer. Appl Opt 32, 4282–4284 (1993). doi: 10.1364/AO.32.004282 [22] Monzón JJ, Sánchez-Soto LL. Reflected fringes in a Fabry-Perot interferometer with absorbing coatings. J Opt Soc Am A 12, 132–136 (1995). [23] Kim Y, Neikirk DP. Design for manufacture of micromachined Fabry-pérot cavity-based sensors. Sensors Actuat A:Phys 50, 141–146 (1995). doi: 10.1016/0924-4247(96)80098-7 [24] Tian JJ, Jiao YZ, Fu Q, Ji SB, Li ZG et al. A Fabry-Perot interferometer strain sensor based on concave-core photonic crystal fiber. J Lightwave Technol 36, 1952–1958 (2018). doi: 10.1109/JLT.2018.2797104 [25] Wang ZY, Clark JK, Ho YL, Vilquin B, Daiguji H et al. Narrowband thermal emission realized through the coupling of cavity and Tamm plasmon resonances. ACS Photonics 5, 2446–2452 (2018). doi: 10.1021/acsphotonics.8b00236 [26] Molesky S, Lin Z, Piggott AY, Jin WL, Vucković J et al. Inverse design in nanophotonics. Nat Photonics 12, 659–670 (2018). doi: 10.1038/s41566-018-0246-9 [27] Ma W, Liu ZC, Kudyshev ZA, Boltasseva A, Cai WS et al. Deep learning for the design of photonic structures. Nat Photonics 15, 77–90 (2021). doi: 10.1038/s41566-020-0685-y [28] Wiecha PR, Arbouet A, Girard C, Muskens OL. Deep learning in nano-photonics: inverse design and beyond. Photonics Res 9, B182–B200 (2021). doi: 10.1364/PRJ.415960 [29] Liao MH, Zheng SS, Pan SX, Lu DJ, He WQ et al. Deep-learning-based ciphertext-only attack on optical double random phase encryption. Opto-Electron Adv 4, 200016 (2021). doi: 10.29026/oea.2021.200016 [30] Mur G. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Trans Electromagn Compat EMC-23, 377–382 (1981). [31] Moharam MG, Gaylord TK. Rigorous coupled-wave analysis of planar-grating diffraction. J Opt Soc Am 71, 811–818 (1981). doi: 10.1364/JOSA.71.000811 [32] Shi Y, Li W, Raman A, Fan SH. Optimization of multilayer optical films with a memetic algorithm and mixed integer programming. ACS Photonics 5, 684–691 (2018). doi: 10.1021/acsphotonics.7b01136 [33] Zhang ZY, Huang BJ, Zhang Z, Cheng CT, Liu HW et al. Highly efficient vertical fiber interfacing grating coupler with bilayer anti-reflection cladding and backside metal mirror. Opt Laser Technol 90, 136–143 (2017). doi: 10.1016/j.optlastec.2016.08.001 [34] Joshi S, Kiani A. Hybrid artificial neural networks and analytical model for prediction of optical constants and bandgap energy of 3D nanonetwork silicon structures. Opto-Electron Adv 4, 210039 (2021). doi: 10.29026/oea.2021.210039 [35] Malkiel I, Mrejen M, Nagler A, Arieli U, Wolf L et al. Plasmonic nanostructure design and characterization via Deep Learning. Light Sci Appl 7, 60 (2018). doi: 10.1038/s41377-018-0060-7 [36] Ginis V, Piccardo M, Tamagnone M, Lu JS, Qiu M et al. Remote structuring of near-field landscapes. Science 369, 436–440 (2020). doi: 10.1126/science.abb6406 [37] Hu YQ, Luo XH, Chen YQ, Liu Q, Li X et al. 3D-Integrated metasurfaces for full-colour holography. Light Sci Appl 8, 86 (2019). doi: 10.1038/s41377-019-0198-y [38] Estakhri NM, Edwards B, Engheta N. Inverse-designed metastructures that solve equations. Science 363, 1333–1338 (2019). doi: 10.1126/science.aaw2498 [39] Guo DG, Lin RM, Wang WJ. Modelling and optimization of a Fabry–Perot microcavity for sensing applications. J Opt:Pure Appl Opt 6, 1027–1035 (2004). doi: 10.1088/1464-4258/6/11/005 [40] Passaglia E, Stromberg RR, Kruger J. Ellipsometry in the Measurement of Surfaces and Thin Films: Symposium Proceedings (US National Bureau of Standards, Washington, 1964). [41] Ciesielski A, Skowronski L, Trzcinski M, Szoplik T. Controlling the optical parameters of self-assembled silver films with wetting layers and annealing. Appl Surf Sci 421, 349–356 (2017). doi: 10.1016/j.apsusc.2017.01.039 [42] Johnson PB, Christy RW. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys Rev B 9, 5056–5070 (1974). doi: 10.1103/PhysRevB.9.5056 -
Supplementary Information
Supplementary information for Inverse design and realization of an optical cavity-based displacement transducer with arbitrary response
-
Access History
Figures(8)
Tables(2)
Article Metrics
Export File
Citation
Lu QB, Xiao QX, Liu CX, Wang YN, Zhu QX et al. Inverse design and realization of an optical cavity-based displacement transducer with arbitrary responses. Opto-Electron Adv 6, 220018 (2023). doi: 10.29026/oea.2023.220018
Format
Content
DownLoad:
-
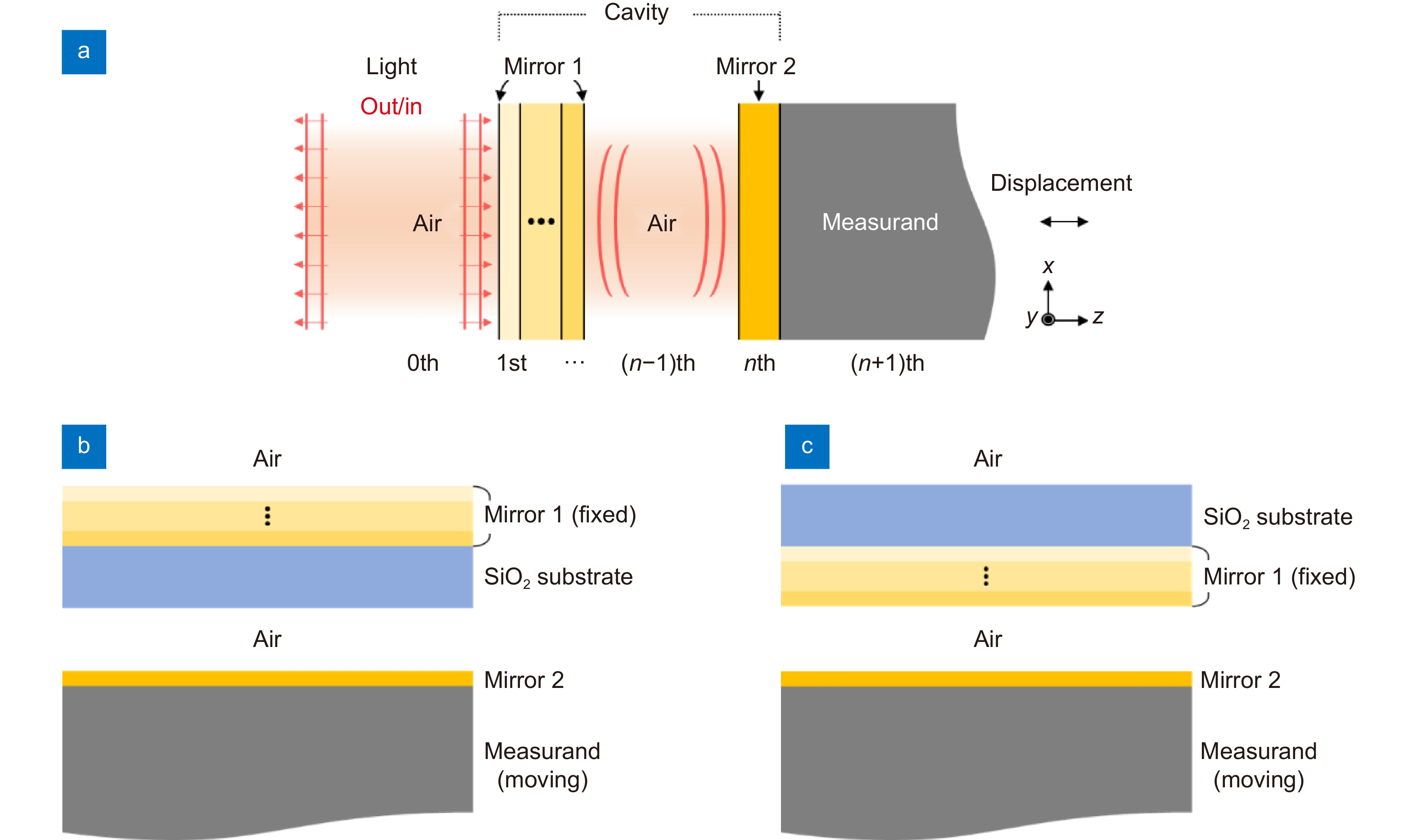
Figure 1.
(a) Schematic diagram of the investigated F-P cavity-based displacement transducer located in air. (b) Low-case of the stratified system. (c) Up-case of the stratified system.
-
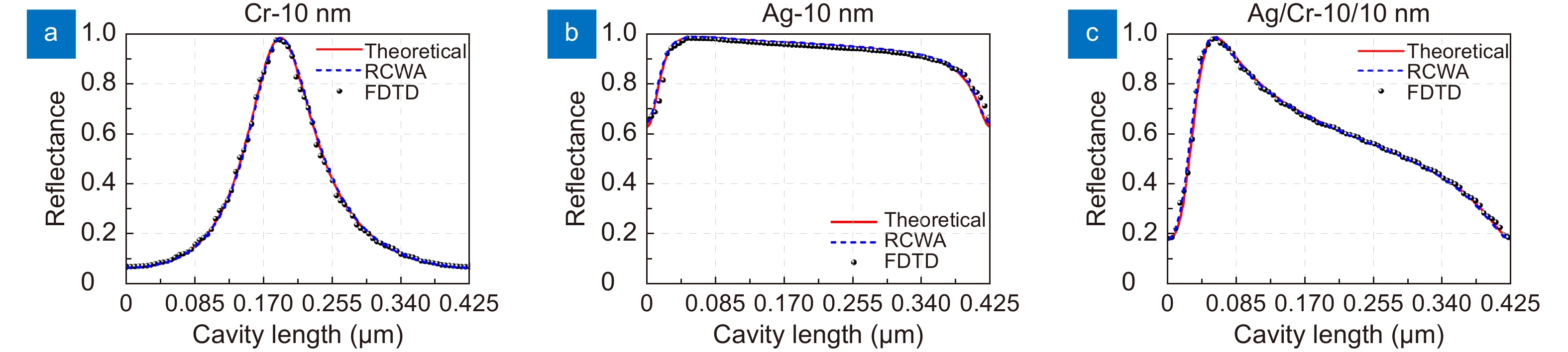
Figure 2.
Comparison of reflectance verse cavity length between the theoretical results and results obtained by RCWA and FDTD for cases of a suspended film of (a) Cr with a thickness of 10 nm, (b) Ag with a thickness of 10 nm and (c) a stack of Ag/Cr with the thickness of 10/10 nm, and the reflector is a 1 μm thick Ag.
-
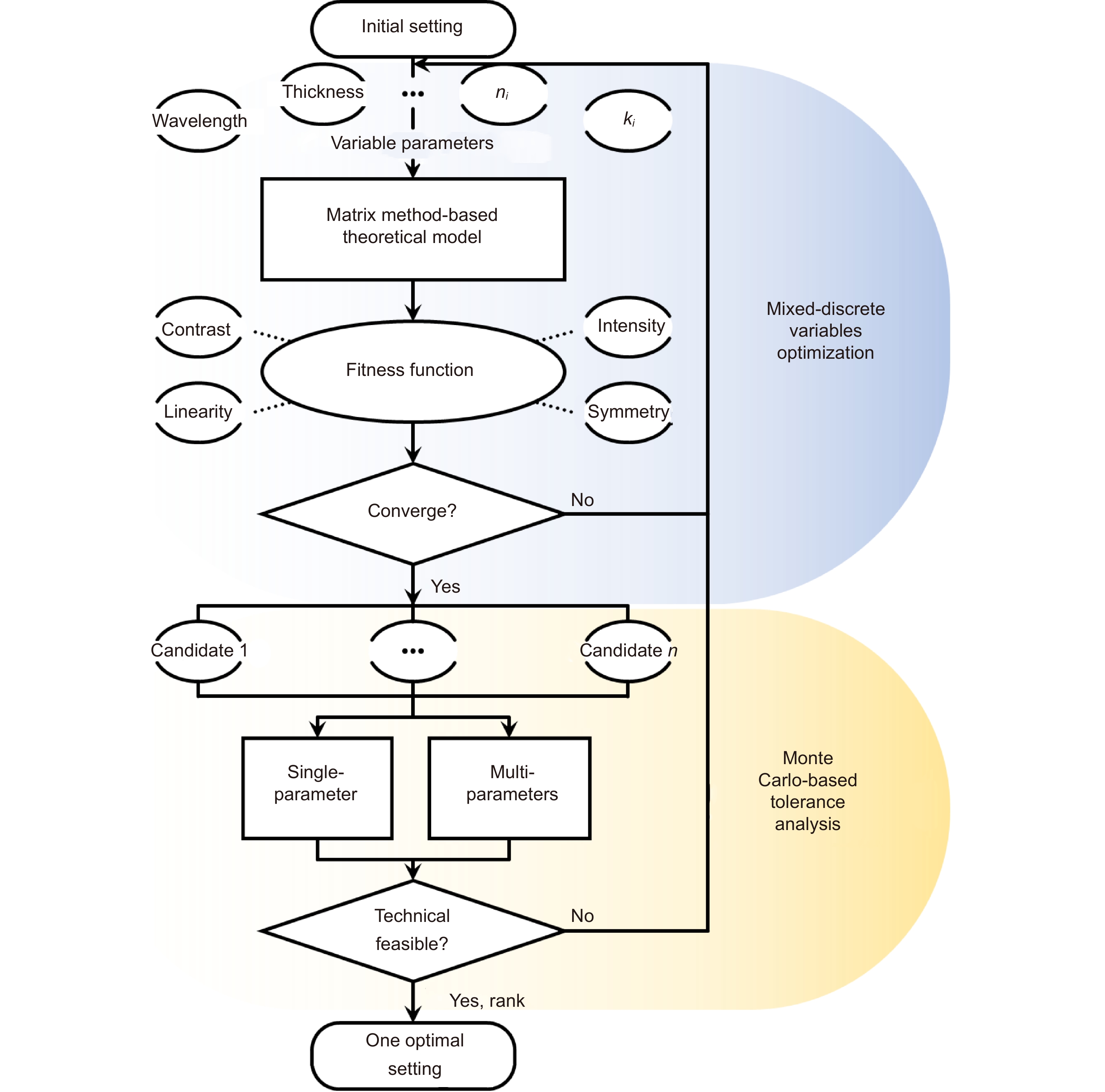
Figure 3.
Inverse design flow of the F-P cavity that contains the mixed-discrete variables optimization and the Monte Carlo-based tolerance analysis, wherein the matrix method-based theoretical model serves as the connection between the variable parameters and the fitness function.
-
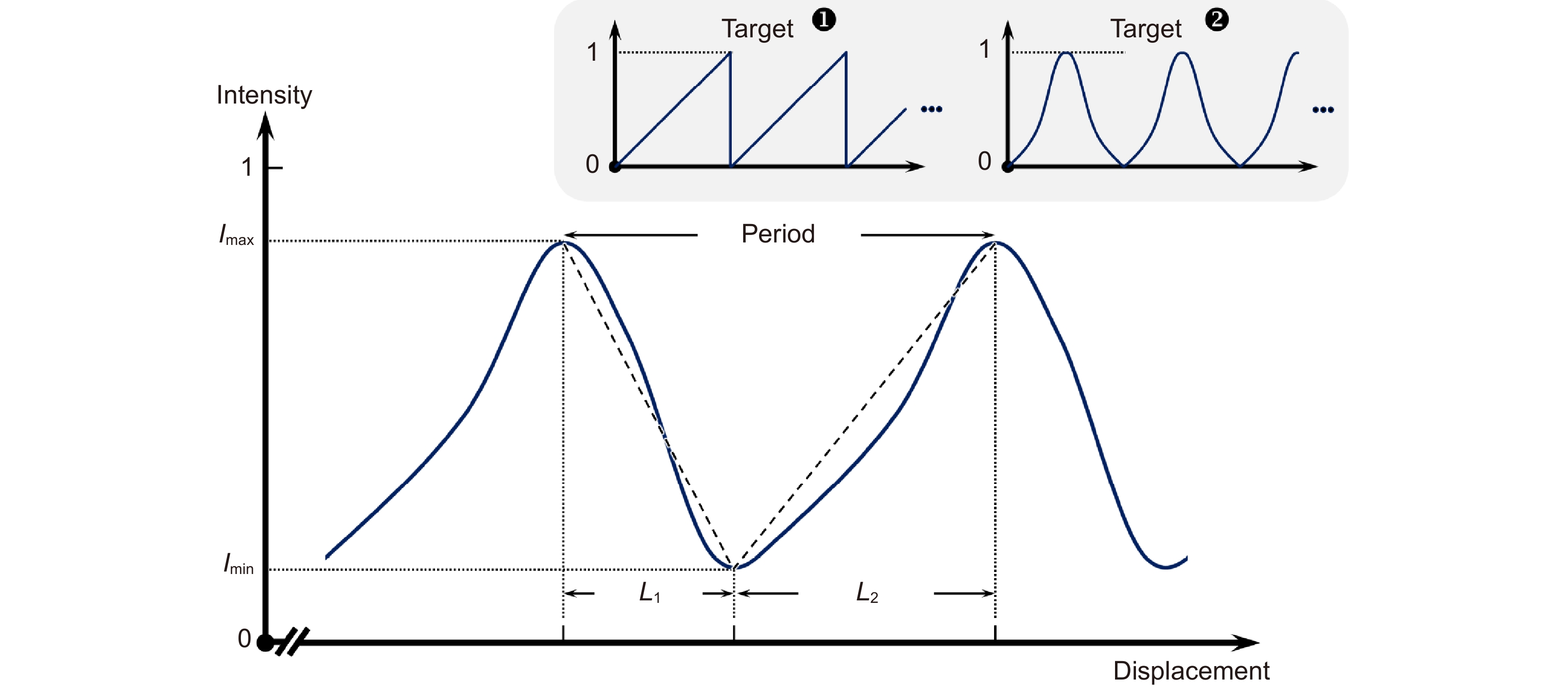
Figure 4.
Illustration of the light intensity response as a function of displacement, and the target responses, a sawtooth-like curve and a perfectly symmetric response, are shown in the inset.
-
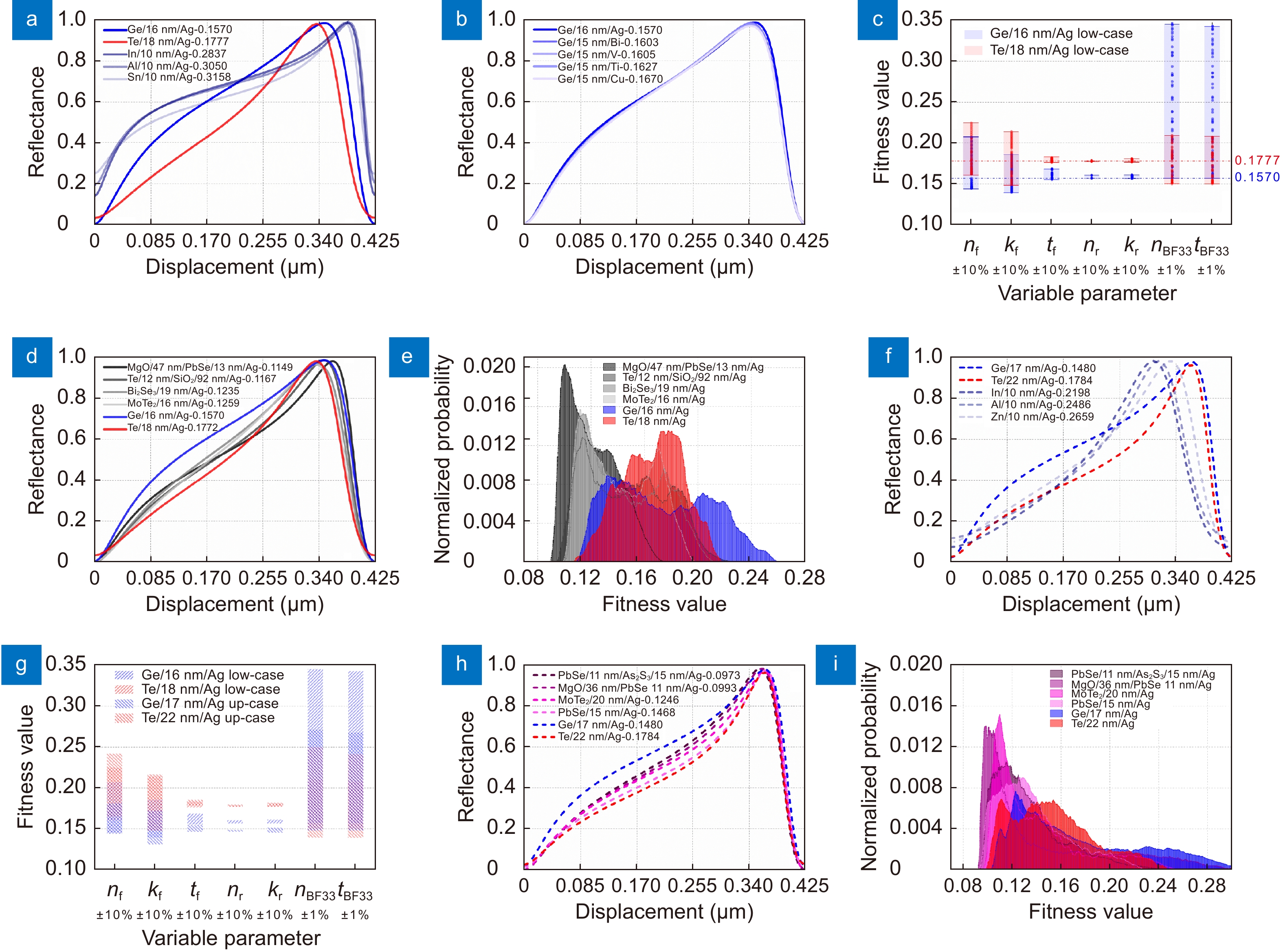
Figure 5.
Optimization results of the sawtooth-like design. (a) Light-displacement responses of 5 primary candidates of the single-layer setting among the simple substance materials for the low-case. (b) Light-displacement responses of the candidates with Ge but different moving mirror materials for the single-layer low-case setting. (c) Single-parameter tolerance analysis results of single-layer low-case settings of Ge and Te, where the circles represent the calculated fitness value for each random variable parameter, the chain dotted lines represent the original fitness values, and the blocks represent the variation range of the fitness values. (d) Light-displacement responses of primary candidates of both two-layers and single-layer settings among the whole materials for the low-case. (e) Histogram of multi-parameter tolerance analysis results of all candidates for the low-case. (f) Light-displacement responses of 5 primary candidates of the single-layer setting among the simple substance materials for the up-case. (g) Comparison of single-parameter tolerance analysis results of Ge and Te for both low- and up-cases, where blue and red colors represent the Ge and Te results, and left and right slashes represent low- and up-cases, respectively. (h) Light-displacement responses of primary candidates of both two-layers and single-layer settings among the whole materials for the up-case. (i) Histogram of multi-parameter tolerance analysis results of all candidates for the up-case.
-
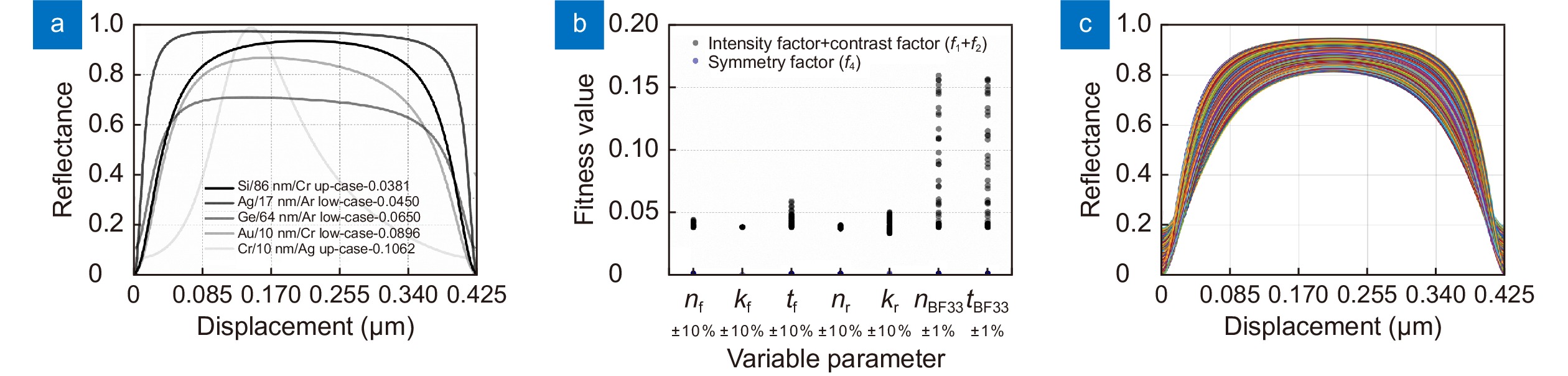
Figure 6.
Optimization results of the symmetric design. (a) Light-displacement responses of 5 primary candidates among the simple substance materials for the single-layer setting. (b) Single-parameter tolerance analysis results of Si/86 nm/Cr up-case setting. (c) Responses of all multi-parameter tolerance analysis results.
-
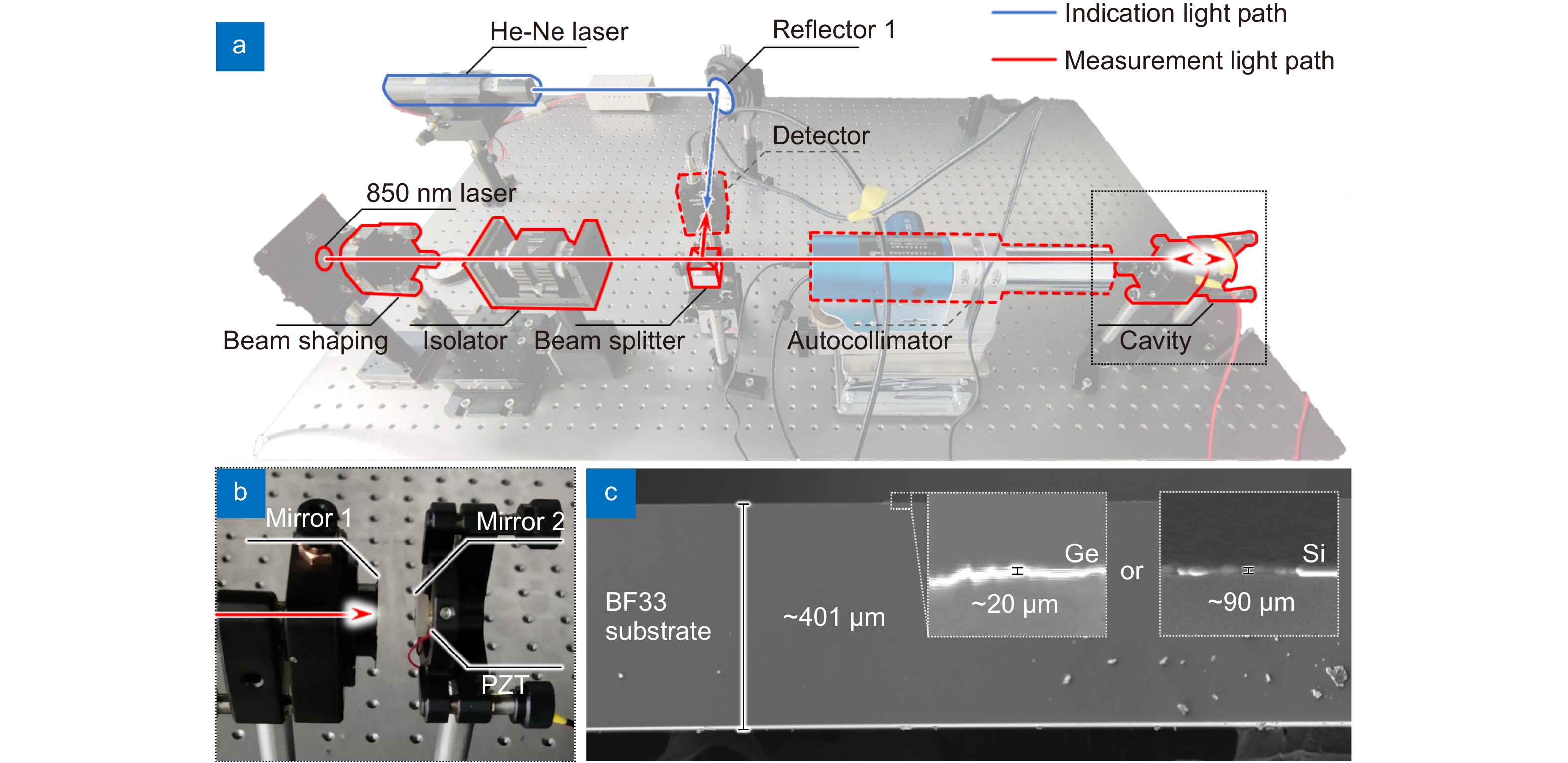
Figure 7.
(a) Experimental configuration of the cavity-based displacement measurement. (b) Magnified view of the length tunable F-P cavity. (c) Cross-sectional view of mirror 1, along with the SEM images of the Ge film and the Si film in the inset.
-
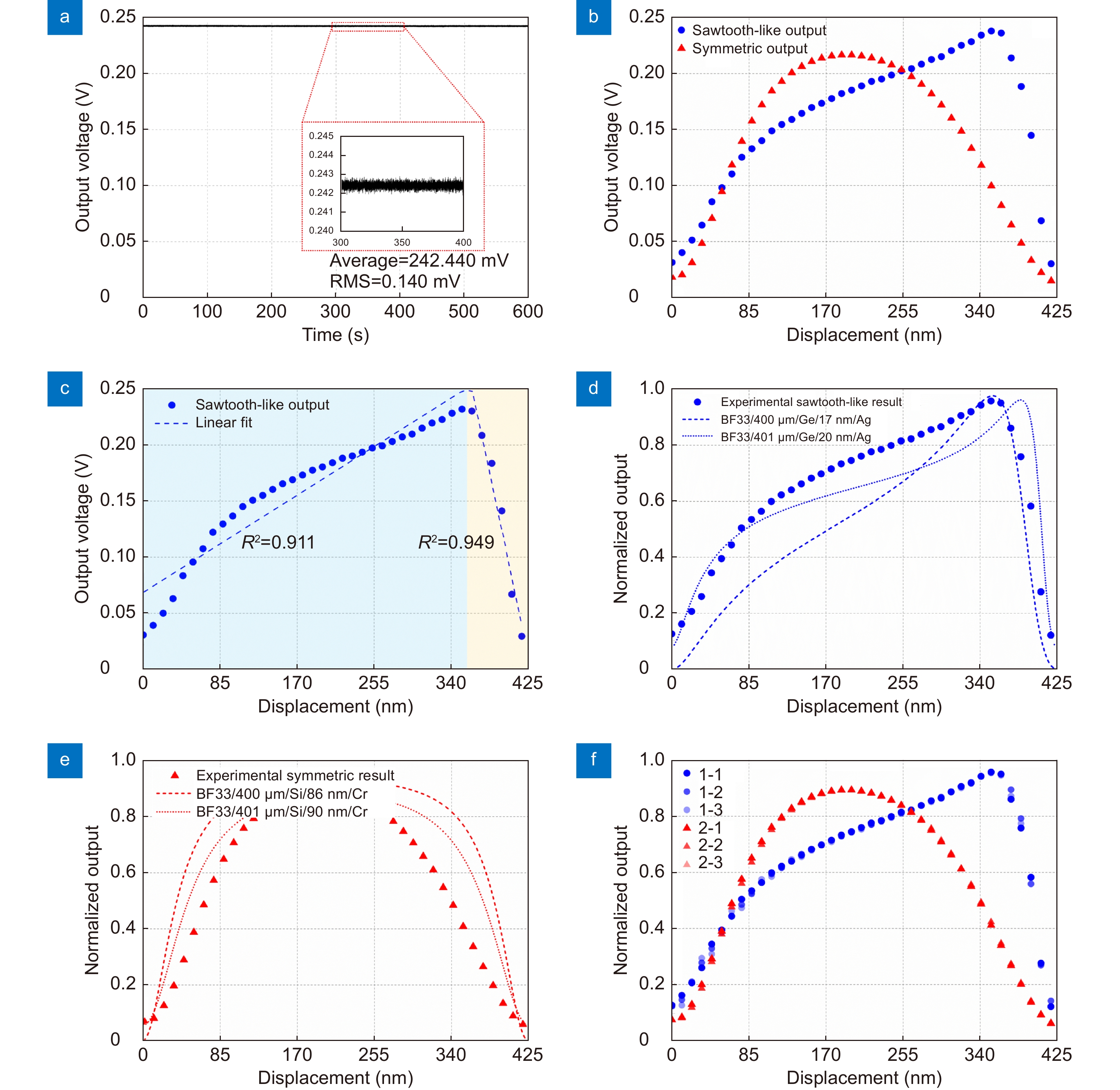
Figure 8.
Experimental data. (a) Output voltage of the incident light as a function of time. (b) Static outputs of the optical cavities versus displacement for two designs, each point denotes an average value at a specific displacement. (c) Linear fit of the experimental result of the sawtooth-like design. (d) Comparison of the experimental results of the sawtooth-like design and theoretical results of optimal setting and setting considering tolerance. (e) Comparison of the experimental results of the symmetric design and theoretical results of optimal setting and setting considering tolerance. (f) Results of the repeatability test for two designs.
