E-mail Alert
RSS
| Citation: |
Liu T, Li H, He T, Fan CZ, Yan ZJ et al. Ultra-high resolution strain sensor network assisted with an LS-SVM based hysteresis model. Opto-Electron Adv 4, 200037 (2021). doi: 10.29026/oea.2021.200037
|
Original Article Open Access
Ultra-high resolution strain sensor network assisted with an LS-SVM based hysteresis model
-
Abstract
Optical fiber sensor network has attracted considerable research interests for geoscience applications. However, the sensor capacity and ultra-low frequency noise limits the sensing performance for geoscience data acquisition. To achieve a high-resolution and lager sensing capacity, a strain sensor network is proposed based on phase-sensitive optical time domain reflectometer (φ-OTDR) technology and special packaged fiber with scatter enhanced points (SEPs) array. Specifically, an extra identical fiber with SEPs array which is free of strain is used as the reference fiber, for compensating the ultra-low frequency noise in the φ-OTDR system induced by laser source frequency shift and environment temperature change. Moreover, a hysteresis operator based least square support vector machine (LS-SVM) model is introduced to reduce the compensation residual error generated from the thermal hysteresis nonlinearity between the sensing fiber and reference fiber. In the experiment, the strain sensor network possesses a sensing capacity with 55 sensor elements. The phase bias drift with frequency below 0.1 Hz is effectively compensated by LS-SVM based hysteresis model, and the signal to noise ratio (SNR) of a strain vibration at 0.01 Hz greatly increases by 24 dB compared to that of the sensing fiber for direct compensation. The proposed strain sensor network proves a high dynamic resolution of 10.5 pε·Hz-1/2 above 10 Hz, and ultra-low frequency sensing resolution of 166 pε at 0.001 Hz. It is the first reported a large sensing capacity strain sensor network with sub-nε sensing resolution in mHz frequency range, to the best of our knowledge. -
-
References
[1] Bergen KJ, Johnson PA, de Hoop MV, Beroza GC. Machine learning for data-driven discovery in solid Earth geoscience. Science 363, eaau0323 (2019). doi: 10.1126/science.aau0323 [2] Liu QW, Tokunaga T, He ZY. Ultra-high-resolution large-dynamic-range optical fiber static strain sensor using Pound–Drever–Hall technique. Opt Lett 36, 4044–4046 (2011). doi: 10.1364/OL.36.004044 [3] Asheden CL, Lindsay JM, Sherburn S, Smith IEM, Miller CA et al. Some challenges of monitoring a potentially active volcanic field in a large urban area: Auckland volcanic field, New Zealand. Nat Hazards 59, 507–528 (2011). doi: 10.1007/s11069-011-9773-0 [4] Davis EE, Heesemann M, Lambert A, He JH. Seafloor tilt induced by ocean tidal loading inferred from broadband seismometer data from the Cascadia subduction zone and Juan de Fuca Ridge. Earth Planet Sci Lett 463, 243–252 (2017). doi: 10.1016/j.jpgl.2017.01.042 [5] Kimura T, Murakami H, Matsumoto T. Systematic monitoring of instrumentation health in high-density broadband seismic networks. Earth Planets Space 67, 55 (2015). doi: 10.1186/s40623-015-0226-y [6] Huang WZ, Zhang WT, Luo YB, Li L, Liu WY et al. Broadband FBG resonator seismometer: principle, key technique, self-noise, and seismic response analysis. Opt Express 26, 10705–10715 (2018). doi: 10.1364/OE.26.010705 [7] Jiang P, Ma LN, Hu ZL, Hu YM. Low-crosstalk and polarization-independent inline interferometric fiber sensor array based on fiber Bragg gratings. J Lightw Technol 34, 4232–4239 (2016). doi: 10.1109/JLT.2016.2597301 [8] Zhao ZY, Tang M, Lu C. Distributed multicore fiber sensors. Opto-Electron Adv 3, 190024 (2020). [9] Wang BZ, Ba DX, Chu Q, Qiu LQ, Zhou DW et al. High-sensitivity distributed dynamic strain sensing by combining Rayleigh and Brillouin scattering. Opto-Electron Adv 3, 200013 (2020). doi: 10.29026/oea.2020.200013 [10] Jousset P, Reinsch T, Ryberg T, Blanck H, Clarke A et al. Dynamic strain determination using fibre-optic cables allows imaging of seismological and structural features. Nat Commun 9, 2509 (2018). doi: 10.1038/s41467-018-04860-y [11] Ajo-Franklin JB, Dou S, Lindsey NJ, Monga I, Tracy C et al. Distributed acoustic sensing using dark fiber for near-surface characterization and broadband seismic event detection. Sci Rep 9, 1328 (2019). doi: 10.1038/s41598-018-36675-8 [12] Masoudi A, Newson TP. Contributed review: distributed optical fibre dynamic strain sensing. Rev Sci Instrum 87, 011501 (2016). doi: 10.1063/1.4939482 [13] Wang ZN, Zhang L, Wang S, Xue NT, Peng F et al. Coherent Φ-OTDR based on I/Q demodulation and homodyne detection. Opt Express 24, 853–858 (2016). doi: 10.1364/OE.24.000853 [14] Chen D, Liu QW, He ZY. High-fidelity distributed fiber-optic acoustic sensor with fading noise suppressed and sub-meter spatial resolution. Opt Express 26, 16138–16146 (2018). doi: 10.1364/OE.26.016138 [15] Wu MS, Fan XY, Liu QW, He HY. Highly sensitive quasi-distributed fiber-optic acoustic sensing system by interrogating a weak reflector array. Opt Lett 43, 3594–3597 (2018). doi: 10.1364/OL.43.003594 [16] Liang GH, Jiang JF, Liu K, Wang S, Xu TH et al. Phase demodulation method based on a dual-identical-chirped-pulse and weak fiber Bragg gratings for quasi-distributed acoustic sensing. Photonics Res 8, 1093–1099 (2020). doi: 10.1364/PRJ.389400 [17] Mateeva A, Lopez J, Chalenski D, Tatanova M, Zwartjes P et al. 4D DAS VSP as a tool for frequent seismic monitoring in deep water. Leading Edge 36, 995–1000 (2017). doi: 10.1190/tle36120995.1 [18] Zhong X, Zhang CX, Li LJ, Liang S, Li Q et al. Influences of laser source on phase-sensitivity optical time-domain reflectometer-based distributed intrusion sensor. Appl Opt 53, 4645–4650 (2014). doi: 10.1364/AO.53.004645 [19] Zhu F, Zhang XP, Xia L, Guo Z, Zhang YX. Active compensation method for light source frequency drifting in Φ-OTDR sensing system. IEEE Photonic Technol Lett 27, 2523–2526 (2015). doi: 10.1109/LPT.2015.2468075 [20] Yuan Q, Wang F, Liu T, Liu Y, Zhang YX et al. Compensating for influence of laser-frequency-drift in phase-sensitive OTDR with twice differential method. Opt. Express 27, 3664–3671 (2019). doi: 10.1364/OE.27.003664 [21] Sun QZ, Yan ZJ, Liu DM, Zhang L. Optical fiber sensor network and industrial applications. In: Peng GD. Handbook of Optical Fibers 1–46 (Springer, 2019); https://doi.org/10.1007/978-981-10-1477-2_20-1. [22] Li H, Sun QZ, Liu T, Fan CZ, He T et al. Ultra-high sensitive quasi-distributed acoustic sensor based on coherent OTDR and cylindrical transducer. J Lightw Technol 38, 929–938 (2020). doi: 10.1109/JLT.2019.2951624 [23] Liu T, Li H, Ai F, Wang J, Fan CZ et al. Ultra-high resolution distributed strain sensing based on phase-OTDR. In Proc. Optical Fiber Communications Conference (IEEE, 2019). https://doi.org/10.1364/OFC.2019.Th2A.16. [24] Ai F, Sun QZ, Zhang W, Liu T, Yan ZJ et al. Wideband fully-distributed vibration sensing by using UWFBG based coherent OTDR. In Proc. Optical Fiber Communications Conference (OSA, 2017). https://doi.org/10.1364/OFC.2017.W2A.19. [25] Bobbio S, Milano G, Serpico C, Visone C. Models of magnetic hysteresis based on play and stop hysterons. IEEE Trans Magn 33, 4417–4426 (1997). doi: 10.1109/20.649875 [26] Ge P, Jouaneh M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis Eng 20, 99–111 (1997). doi: 10.1016/S0141-6359(97)00014-7 [27] Brokate M, Sprekels J. Hysteresis and Phase Transitions (Springer, New York, 1996). [28] Suykens JAK, Vandewalle J, De Moor B. Optimal control by least squares support vector machines. Neural Netw 14, 23–35 (2001). doi: 10.1016/S0893-6080(00)00077-0 [29] Vapnik V. Statistical Learning Theory (Johan Wiley & Sons, New York, 1998). [30] Shirley ME, Venkataraman R. On the identification of Preisach measures. Proc SPIE 5049, 326–336 (2003). doi: 10.1117/12.499462 [31] Stakvik JÅ, Ragazzon MRP, Eielsen A A, Gravdahl JT. On implementation of the Preisach model: identification and inversion for hysteresis compensation. Model, Ident Control 36, 133–142 (2015). doi: 10.4173/mic.2015.3.1 -
Access History
Figures(10)
Article Metrics
Export File
Citation
Liu T, Li H, He T, Fan CZ, Yan ZJ et al. Ultra-high resolution strain sensor network assisted with an LS-SVM based hysteresis model. Opto-Electron Adv 4, 200037 (2021). doi: 10.29026/oea.2021.200037
Format
Content
DownLoad:
-
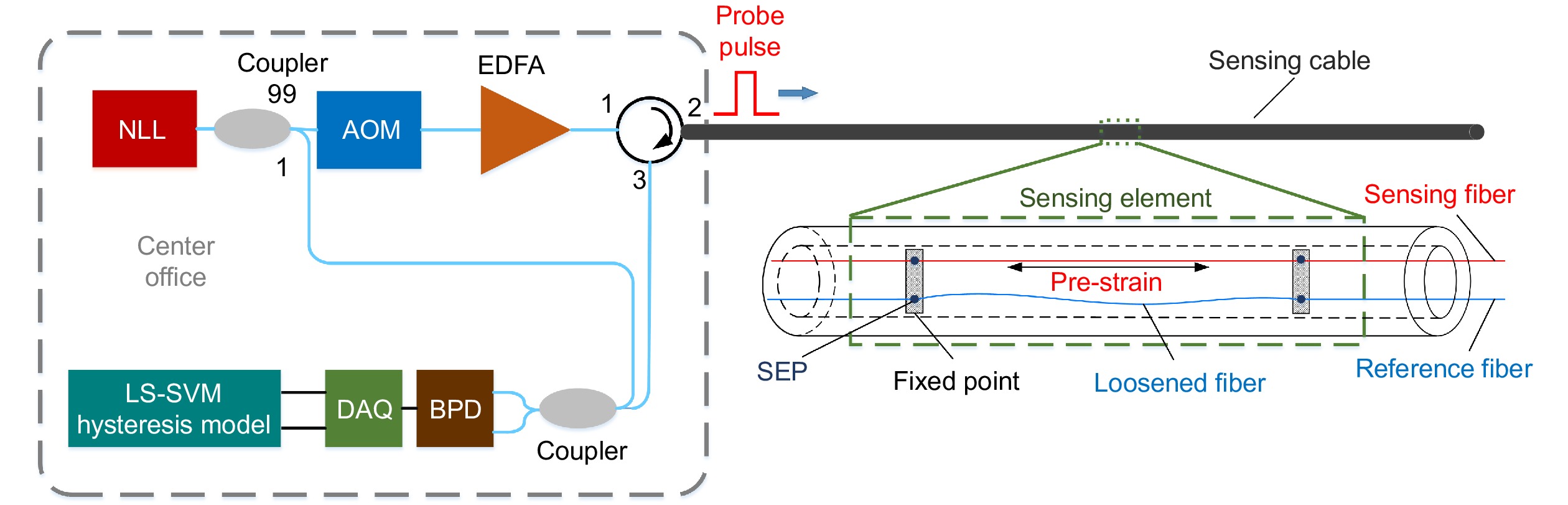
Figure 1.
Schematic diagram of the proposed high-resolution strain sensor network.
-
Figure 2.
(a) Phase change induced by laser frequency shift. (b) Relationship between the reference channel and sensing channel for laser frequency shift.
-
Figure 3.
(a) Phase change induced by temperature fluctuation. (b, c) Enlarged images for phase change. (d) Relationship between the reference channel and sensing channel for temperature fluctuation.
-
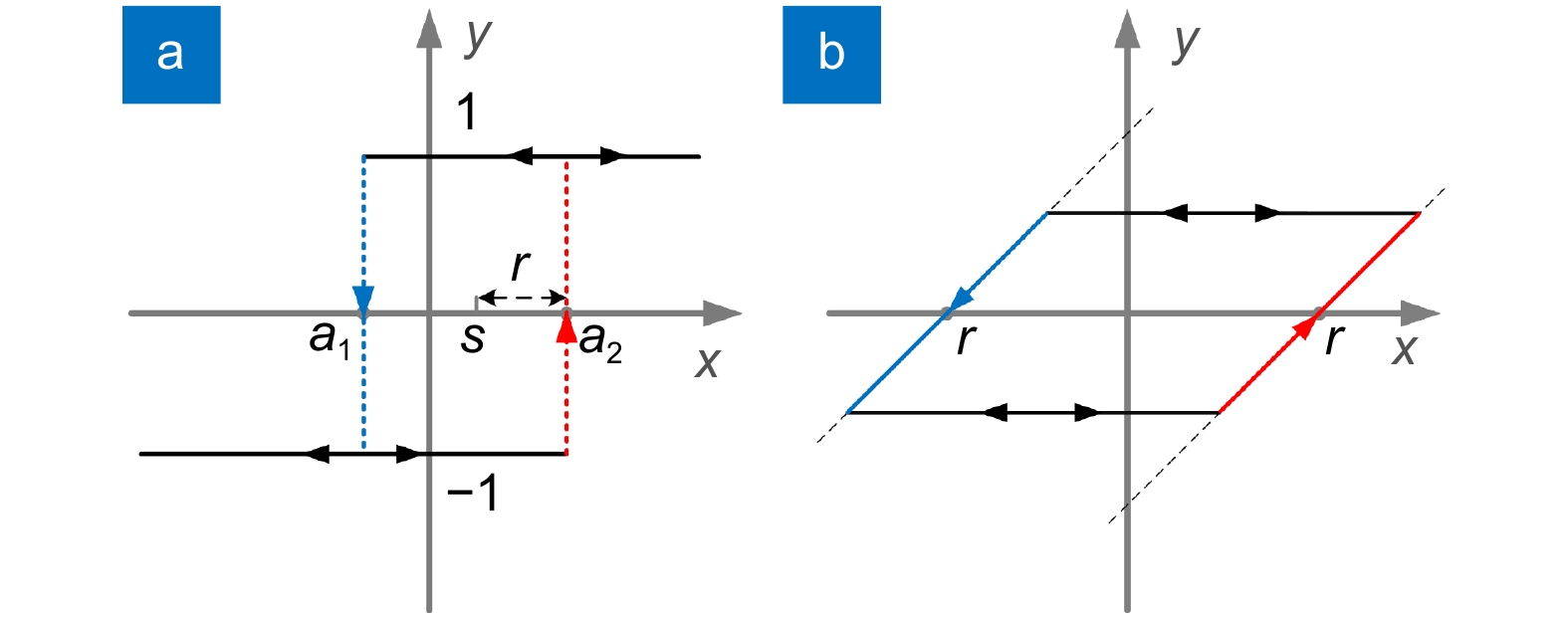
Figure 4.
Hysteresis operator. (a) Relay operator. (b) Play operator.
-
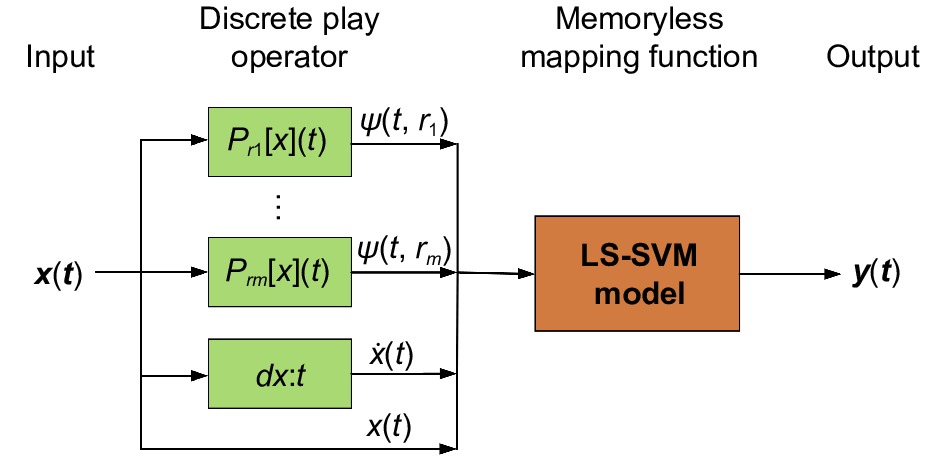
Figure 5.
Block diagram of the LS-SVM based hysteresis model.
-
Figure 6.
(a) Received beat frequency signal. (b) Beat frequency signal of sensor element 55 and 54.
-
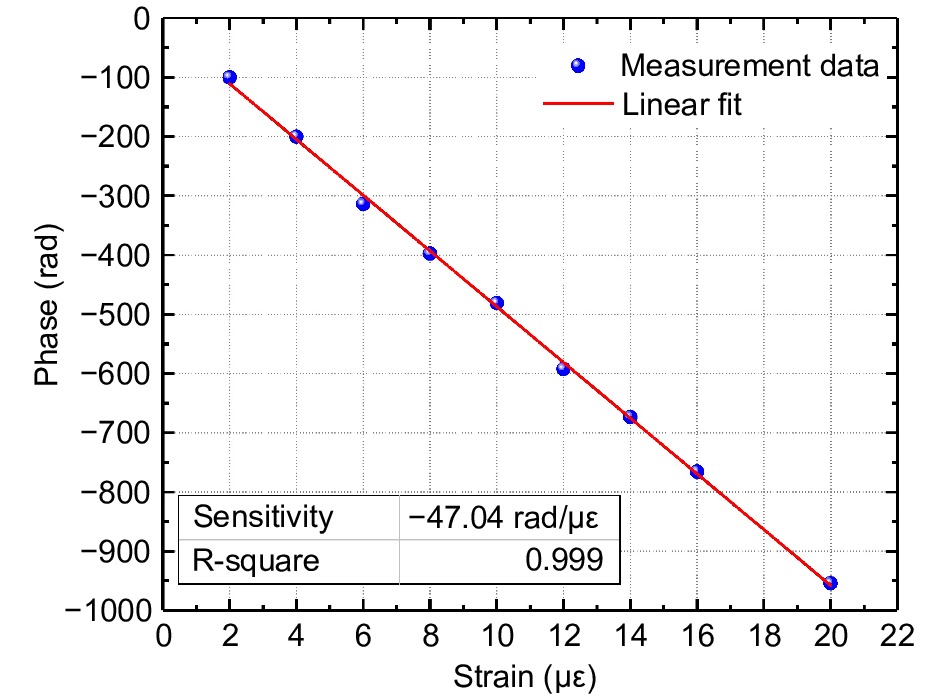
Figure 7.
The relationship between phase change and strain.
-
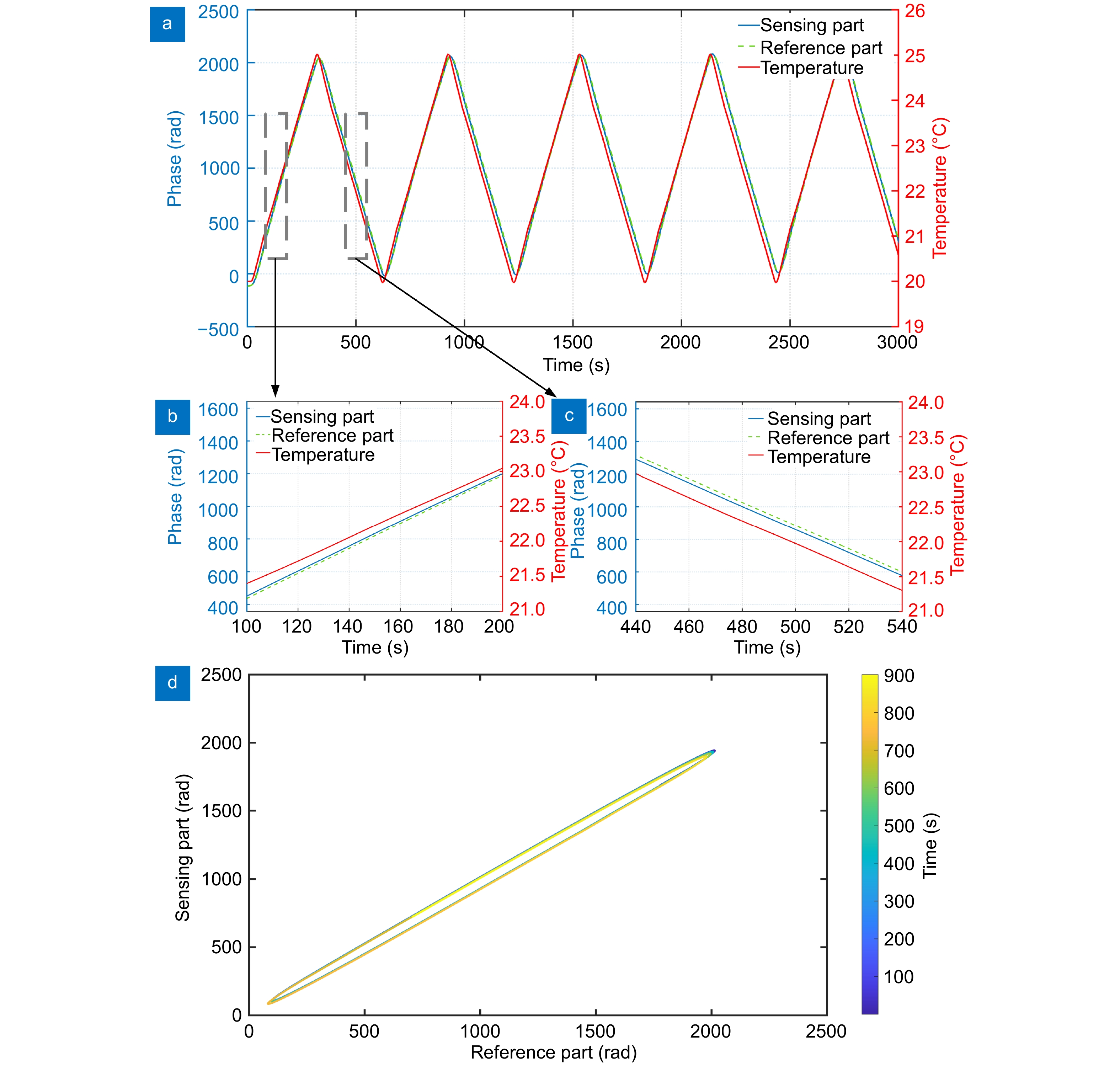
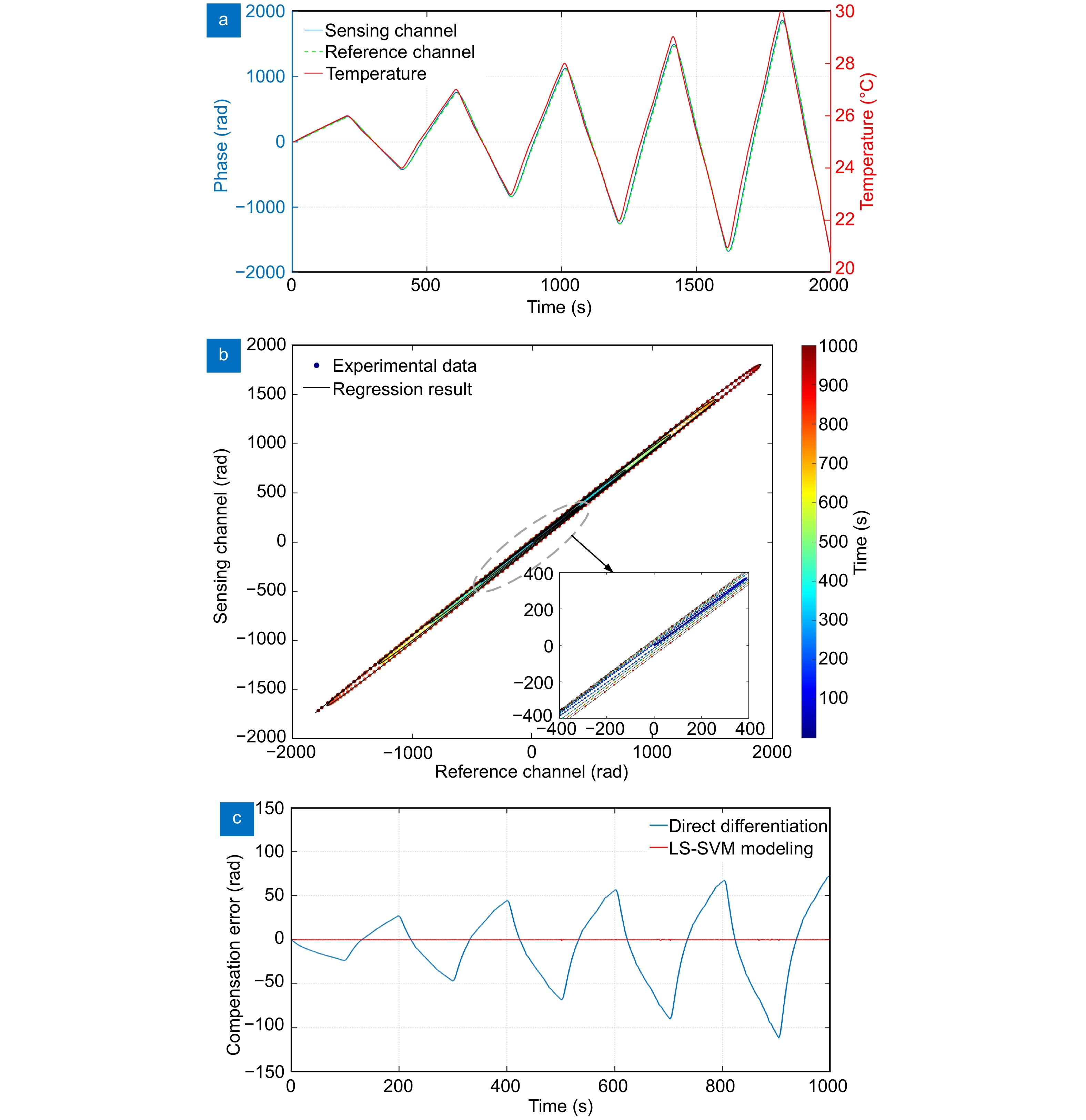
Figure 8.
(a) Temperature change waveform and corresponding phase change for model train. (b) Hysteresis loops for temperature change and the regression result. (c) Compensation error.
-
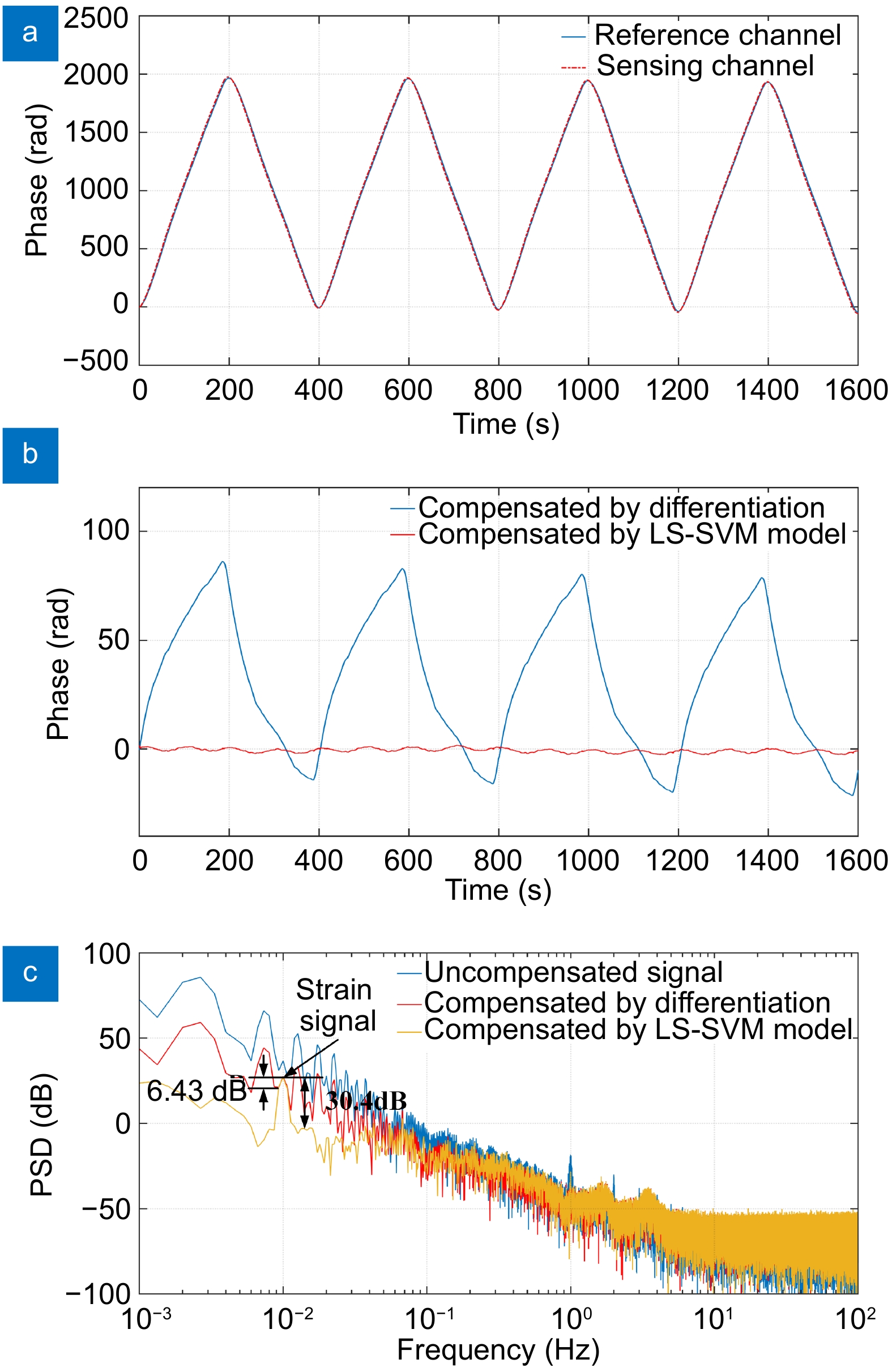
Figure 9.
(a) Original phase signal for temperature change and strain signal. (b) Compensation results for two methods. (c) PSD of the original result and compensation results.
-
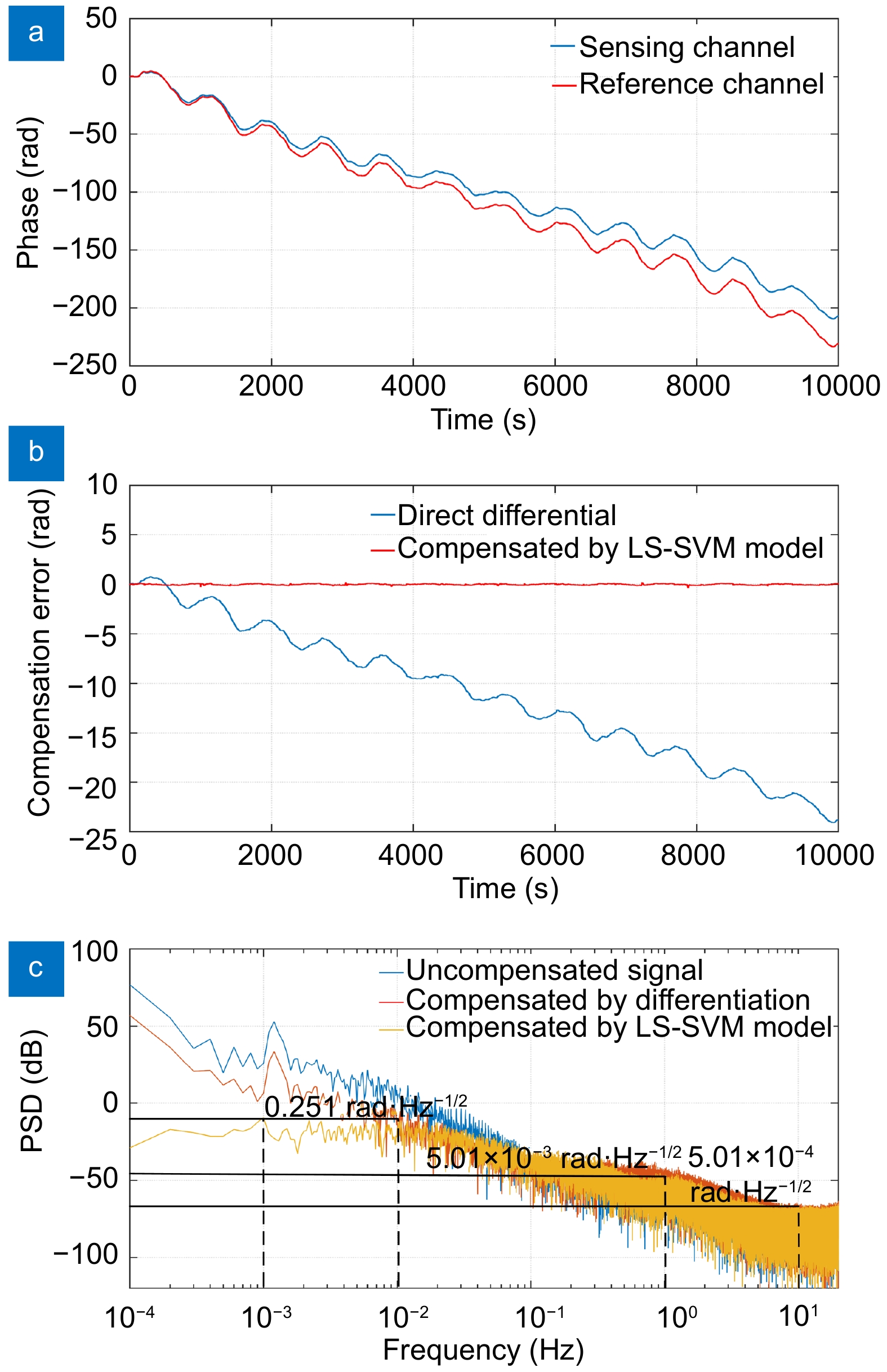
Figure 10.
(a) Original phase signal in a quiet environment. (b) Compensation results for two methods. (c) Noise floor PSD of the original result and compensation results.
